Mie散乱（４）- Rayleigh散乱

１．はじめに

ナノ粒子や高分子を対象としている人は、粒子が大きくなっても散乱光強度は粒子径の6乗に比例すると思い込んでいるかも知れません[1]。それが正しいか、Mie散乱に基づき散乱光強度が粒子径の変化にともなってどう変化するのかを議論します。

２．前提とする光学系

図1 入射光はz軸方向に進み、x-z平面内でx軸方向に直線偏光している。原点に半径がaの球形粒子があり、光を散乱している。散乱光は点Pで検出される。図はφ=90°の場合に相当し、y-z平面が散乱面となる。光散乱装置によく用いられる光学系となる。

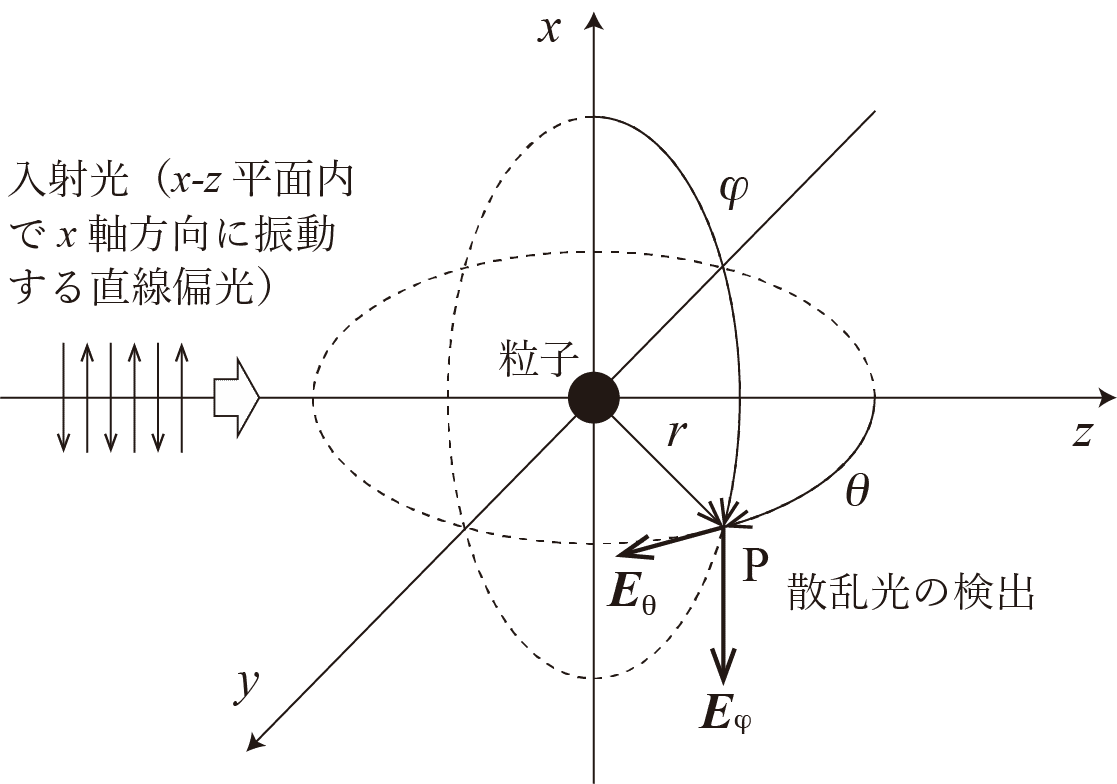
３．Rayleigh散乱 - Mie散乱の特別な場合

3.1 前提条件： 光の波長に比べ粒子径が小さい

$$
x\equiv\displaystyle\frac{2\pi an_0}{\lambda_0}=ka\ll1
$$

$${a}$$：粒子の半径、$${n_0}$$：媒質（溶媒）の屈折率、$${\lambda_0}$$：真空中での光の波長、$${k(\equiv2\pi n_0/\lambda_0)}$$：波数ベクトル$${\boldsymbol k}$$の絶対値

1) 例えば、ナノ粒子（例えば、$${a<50  \mathrm {nm}}$$）などは光の波長に比べると小さい。

3.2 Rayleigh散乱の式 [2,3]

Mie散乱の一般式は[4]、

$$
S_1(\theta)=\sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}\{a_n\pi_n(\cos\theta)+b_n\tau_n(\cos\theta\}
$$

$$
S_2(\theta)=\sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}\{b_n\pi_n(\cos\theta)+a_n\tau_n(\cos\theta\}
$$

でした。$${S_1(\theta)}$$と$${S_2(\theta)}$$の初項だけとり、係数$${a_n}$$と$${b_n}$$を$${x}$$のべき級数展開して、$${x}$$の最小の次数だけとると次式が得られます：

$$
i_1(\theta)＝|S_1(\theta)|^2=(ka)^6\left | \displaystyle\frac{m^2-1}{m^2+2}\right |^2,       (ka\ll1)                                         (1)
$$

$$
i_2(\theta)＝|S_2(\theta)|^2=(ka)^6\left | \displaystyle\frac{m^2-1}{m^2+2}\right |^2\cos{^2\theta},       (ka\ll1)                        (2)
$$

上記から次式が得られます（[4]参照）：

$$
I(\theta, \varphi)=I_0\displaystyle\frac{a^6}{r^2}\left(\displaystyle\frac{2\pi n_0}{\lambda_0}\right)^4\displaystyle\left|\frac{m^2-1}{m^2+2}\right|^2(\cos^2\theta\cos^2\varphi+\sin^2\varphi)                  (3)
$$

$${I}$$：検出された散乱光強度、$${I_0}$$：入射光強度、$${r}$$：粒子から検出器までの距離、$${m=\displaystyle\frac{n_1}{n_0}}$$：相対屈折率（$${n_1}$$は粒子の屈折率、$${n_0}$$は溶媒の屈折率）

上式から、Rayleigh散乱は、波長$${\lambda_0}$$の4乗に反比例し、粒子の半径$${a}$$または粒子径の6乗に比例することがわかります。

1) 前記事[4]の式を再掲：

$$
I=\displaystyle \frac{I_0F(\theta,\varphi)}{k^2r^2}
$$

$$
F(\theta,\varphi)=i_2(\theta)\cos^2\varphi+i_1(\theta)\sin^2\varphi                                  (4)
$$

2) 自然光は偏光していないから、入射光が自然光の場合は$${\varphi}$$について平均をとって[5]、

$$
I(\theta, \varphi)=I_0\displaystyle\frac{a^6}{r^2}\left(\displaystyle\frac{2\pi n_0}{\lambda_0}\right)^4\displaystyle\left|\frac{m^2-1}{m^2+2}\right|^2\displaystyle\frac{1+\cos^2\theta}{2}
$$

４．散乱光強度の粒子径依存性

4.1 Rayleigh散乱とMie散乱（散乱角 θ=90°）

図2 （○）：厳密に計算したMie散乱、黒曲線：MiePlotで計算したMie散乱[6]、赤直線：式(1)から計算したRayleigh散乱（傾き6）。φ=90°では散乱強度はi1(θ)のみの寄与となる（式(3)）。このケースでは、粒子径が約100 nmを超えるとRayleigh散乱が成り立たなくなる。

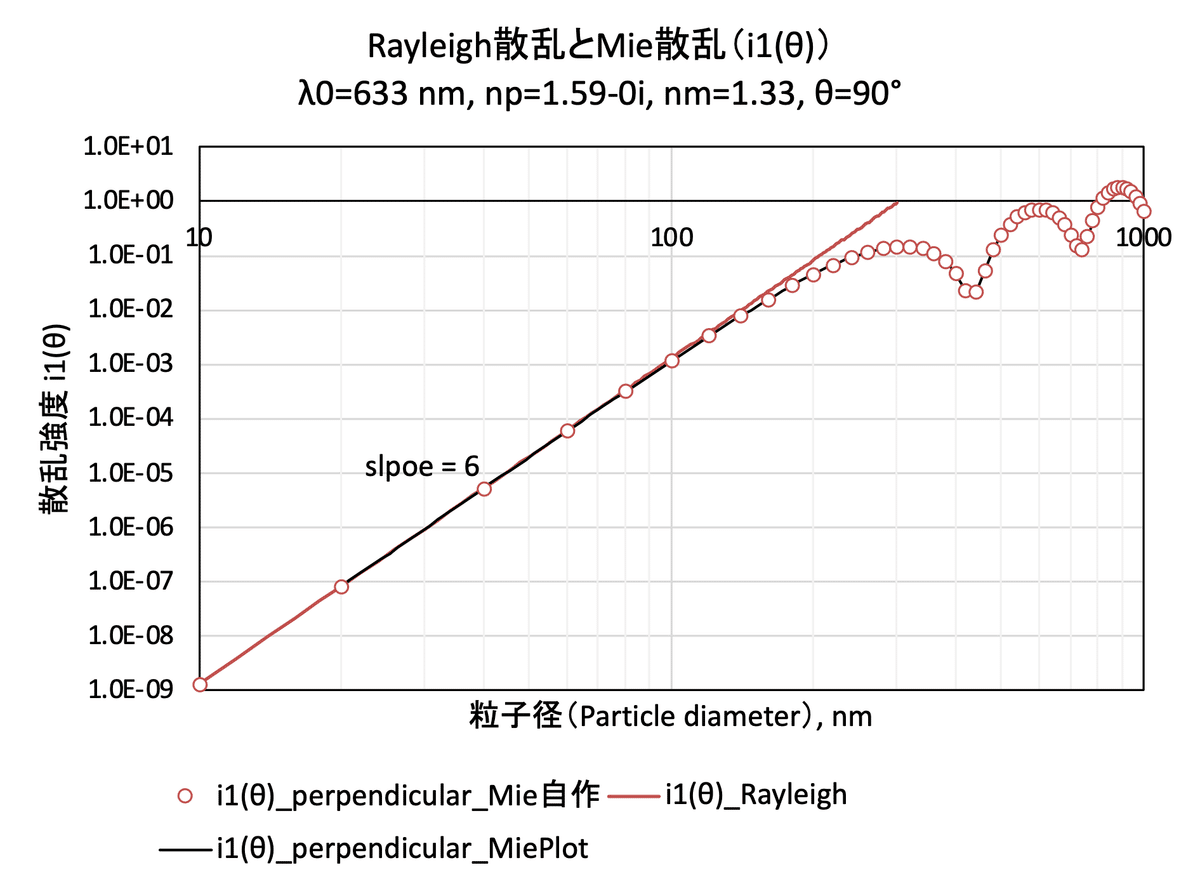
4.2 Rayleigh散乱とMie散乱（散乱角 θ=180°）

図3 （○）：厳密に計算したMie散乱、直線：傾き6のRayleigh散乱（式(1)）。散乱角θ=180°では、i1(θ)とi2(θ)が一致する。このケースでも、粒子径が約100 nmを超えるとRayleigh散乱が成り立たなくなる。100 nmから1 μmの領域では散乱パターンがθ=90°の場合とは異なることに注意する。

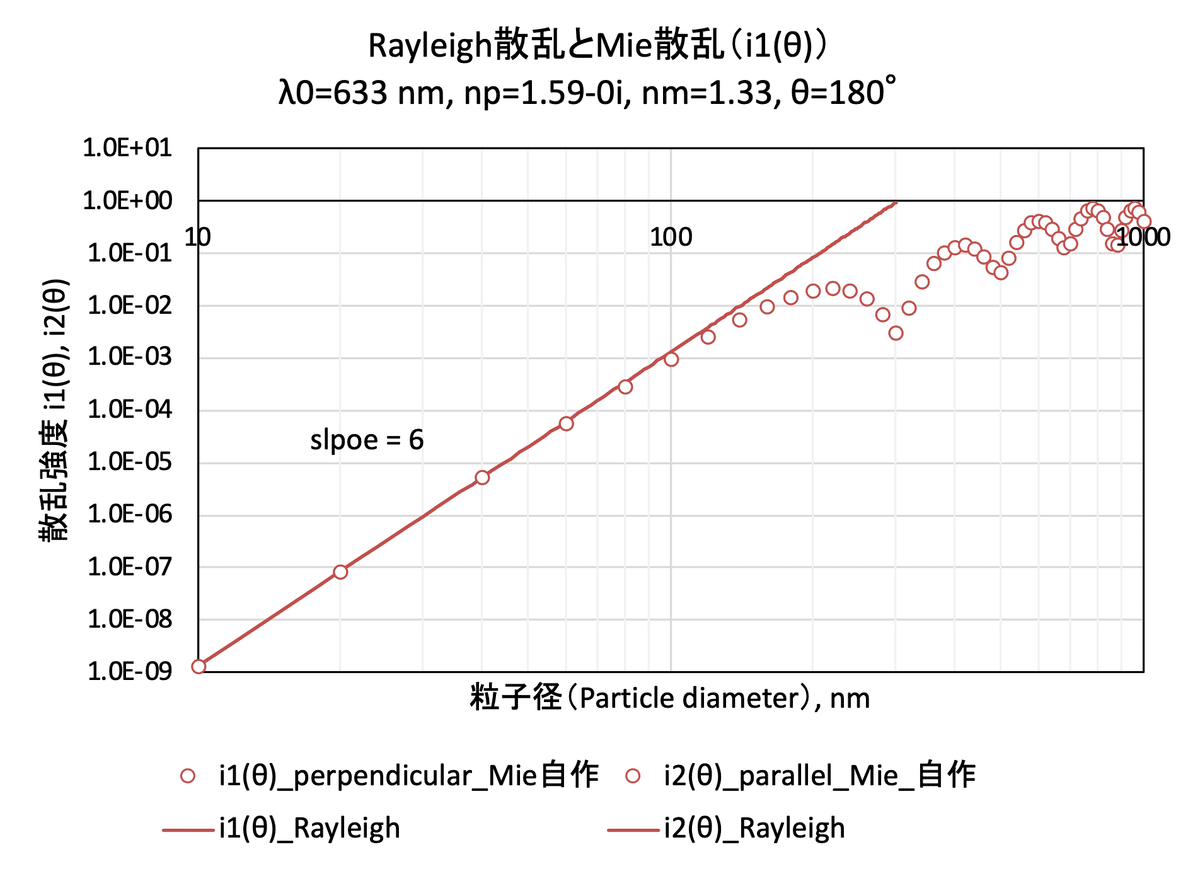
文献

[1] かつての私がそうでした。
[2] いえやすの部屋、"電磁気学 ミー散乱(III) - レイリー散乱"、（Rayleigh散乱の詳しい導出があります。他の記事も参考になります。）
[3] 松山達、"ミーの散乱理論の導出"、粉体工学会誌、2006, 43, 115-124.（Mie散乱の詳しい導出があります。）
[4] Mie散乱（１）- 基本式（noteの記事）
[5]

$$
\langle \sin^2\varphi \rangle =\displaystyle\frac{1}{2\pi}\int_0^{2\pi} \sin^2\varphi \mathrm d\varphi=\frac{1}{2}
$$

$$
\langle \cos^2\varphi \rangle =\displaystyle\frac{1}{2\pi}\int_0^{2\pi} \cos^2\varphi \mathrm d\varphi=\frac{1}{2}
$$

[6] Philip Laven, MiePlot, http://www.philiplaven.com/mieplot.htm

---

【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。