
小角X線散乱(SAXS)(11) - 【演習】球の散乱関数
球の散乱関数(形状因子、干渉因子)を求める問題です。
【演習】球の散乱関数
図1のように、半径が$${R}$$の球がある。球内の電子密度は、$${\rho_0}$$で均一である。

(問1) 全電子数$${N_e}$$を求めよ。
(問2) 構造因子(構造振幅)$${F(h)}$$を求めよ[1]。ただし、$${h}$$は散乱ベクトル$${\boldsymbol{h}}$$の大きさである[1]。
(問3) 散乱強度$${I(h)}$$を求めよ[1]。
(問4) 散乱関数$${P(h)}$$を求めよ[1]
(問5) 回転半径$${R_G}$$を求めよ[1]。
1) 用語の定義については、文献[1]を参考にしてください。
【解説】
(問1) 電子密度は単位体積あたりの電子の数です。球の体積は$${(4\pi /3)R^3}$$だから、
$$
N_e = \dfrac{4\pi}{3} R^3 \rho_0 \;\;\;\;\;\; (答)
$$
(問2) 計算するにあたって、図2のような極座標系$${(r,\; \theta \; \varphi)}$$を使います。球の対称性から、散乱ベクトル$${\boldsymbol{h}}$$を$${z}$$軸にとってもかまわないでしょう。

構造因子(構造振幅)$${F(\boldsymbol{h})}$$から出発します[1]:
$$
F(\boldsymbol{h}) = \displaystyle \int_V \rho(\boldsymbol{r}) e^{-i \boldsymbol{h} \cdot \boldsymbol{r}} \mathrm{d} \boldsymbol{r}
$$
上式に$${\rho(\boldsymbol{r}) = \rho_0}$$を代入し、さらにベクトルの内積に対して、$${\boldsymbol{h} \cdot \boldsymbol{r} = hr \cos \theta}$$とおくと、
$$
F(\boldsymbol{h}) = \rho_0\displaystyle \int_{r=0}^R \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} e^{-ihr\cos \theta} r^2 \sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi
$$
ここで極座標系の体積要素$${r^2 \sin\theta\mathrm{d}r\mathrm{d}\theta\mathrm{d}\varphi}$$を用いました[2]。
被積分関数$${e^{-ihr\cos \theta} r^2 \sin\theta}$$は$${\varphi}$$を含まないから、$${\varphi}$$に関する積分が実行でき、結果は$${2\pi}$$。次に、$${\theta}$$に関する積分を実行します($${[ \cdots ]}$$の中):
$$
F(\boldsymbol{h}) = 2\pi\rho_0\displaystyle \int_{r=0}^R \bigg [\int_{\theta=0}^\pi e^{-ihr\cos \theta} \sin\theta \mathrm{d}\theta \bigg ] r^2 \mathrm{d}r
$$
$${x = \cos\theta}$$とおくと、$${\mathrm{d}x = -\sin\theta \mathrm{d}\theta}$$だから、
$$
\displaystyle \int_{\theta=0}^\pi e^{-ihr\cos \theta} \sin\theta \mathrm{d}\theta = \int_1^{-1} e^{-ihrx} (- \mathrm{d}x) = \int_{-1}^1 e^{-ihrx} \mathrm{d}x \\ =\Big[ \dfrac{e^{-ihrx}}{-ihr} \Big ]_{-1}^1 =\dfrac{e^{-ihr} - e^{ihr}}{-ihr} = \dfrac{2 \sin{hr}}{hr}
$$
ここで、正弦関数(sin)の複素数表現
$$
\sin z = \dfrac{e^{iz}-e^{-iz}}{2i}
$$
を使いました。
こうして、
$$
F(h) = 4\pi\rho_0 \displaystyle \int_0^R r^2 \dfrac{\sin{hr}}{hr} \mathrm{d}r = \dfrac{4\pi\rho_0}{h} \int_0^R r\sin{hr} \mathrm{d}r
$$
構造因子は散乱ベクトル$${\boldsymbol{h}}$$の大きさ$${h}$$の関数になります。
ここで、積分変数の変換をします。$${x=hr}$$とおくと、$${\mathrm{d}r = \mathrm{d}x / h}$$、および$${r=R}$$のとき$${x=hR}$$なので、上式は、
$$
F(h) = \dfrac{4\pi\rho_0}{h} \displaystyle \int_0^{hR} \Big ( \dfrac{x}{h} \Big ) \sin x \Big (\dfrac{\mathrm{d}x}{h} \Big) = \dfrac{4\pi\rho_0}{h^3} \displaystyle \int_0^{hR} x\sin x \mathrm{d}x
$$
になります。部分積分を実施すると[3]、
$$
\displaystyle \int x (-\sin x) \mathrm{d}x = x\cos x - \int \cos x \mathrm{d}x = x\cos{x} - \sin x
$$
になるから、
$$
\displaystyle \int_0^{hR} x\sin x \mathrm{d}x = \Big [ \sin x-x\cos x \Big ]_0^{hR} = \sin{hR} - hR\cos{hR}
$$
よって、問1の答も使って、
$$
F(h) = N_e \dfrac{3(\sin{hR} - hR\cos{hR})}{(hR)^3} \;\;\;\;\;\; (答)
$$
$${x \ll 1}$$のときのべき級数展開を考えます:
$$
\sin x -x\cos x = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \cdots -x\Big ( 1-\dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \cdots \Big ) =\\ = \dfrac{x^3}{3} - \dfrac{x^5}{30} + \cdots
$$
だから、$${hR \ll 1}$$では、$${h}$$の2次の項まで考慮すると、
$$
\dfrac{3(\sin{hR} - hR\cos{hR})}{(hR)^3} = 1 - \dfrac{(hR)^2}{10} + O((hR)^4)\;\;\;\;\;\;\; (1)
$$
となります[4]。したがって、
$$
\displaystyle \lim_{h \to 0} F(h) = N_e \;\;\;\;\;\;\;\;\; (2)
$$
(問3) 散乱強度$${I(h)}$$は、
$$
I(h) = A_e^2 |F(h)|^2 =A_e^2 N_e^2 \Bigg [ \dfrac{3(\sin{hR} - hR\cos{hR})}{(hR)^3} \Bigg ]^2 \;\;\;\;\;\;\; (答)
$$
式(1)を使えば、
$$
I(0) = \displaystyle \lim_{h \to 0} I(h) = A_e^2 N_e^2
$$
(問4) 散乱関数$${P(h)(=I(h)/I(0))}$$は、
$$
P(h) = \Bigg [\dfrac{ 3(\sin{hR} - hR\cos{hR})}{(hR)^3} \Bigg ]^2 \;\;\;\;\;\; (答)
$$
(問5) 式(1)より、
$$
P(h) = \bigg [\dfrac{ 3(\sin{hR} - hR\cos{hR})}{(hR)^3} \bigg ]^2 = \bigg [ 1 - \dfrac{(hR)^2}{10} + O((hR)^4)\bigg ]^2 = \\ = 1-\dfrac{(hR)^2}{5} + \cdots
$$
公式[5]を使って、
$$
\ln P(h) = - \dfrac{3R^2}{5} \times \dfrac{h^2}{3} + \cdots
$$
Guinierの法則[1]は、
$$
\ln P(h) = - \dfrac{R_G^2}{3} h^2 + \cdots
$$
だから、$${h^2}$$の係数を比較すると、
$$
R_G = \sqrt {\dfrac{3}{5}} R \;\;\;\;\;\; (答)
$$
(別法)$${R_G}$$の定義は、
$$
R_G^2 = \dfrac{\int_V \rho(\boldsymbol{r})(\boldsymbol{r} - \boldsymbol{r}_G )^2 \mathrm{d}\boldsymbol{r}}{\int_V \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r}} \;\;\;\;\;\; (3)
$$
球の場合、重心は中心にあると考えられるから、$${\boldsymbol{r}_G = \boldsymbol{0}}$$。
極座標を使うと、
$$
\displaystyle \int_V \rho(\boldsymbol{r})\boldsymbol{r}^2 \mathrm{d}\boldsymbol{r} = \rho_0\int_{r=0}^R \int_{\theta=0}^\pi \int_{\varphi=0}^{2\pi} r^4 \sin\theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\varphi = 4\pi\rho_0 \int_0^R r^4 \mathrm{d}r = \\ = \dfrac{4\pi}{5} R^5 \rho_0
$$
一方、
$$
\displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r} = 全電子数N_e = \dfrac{4\pi}{3}R^3 \rho_0
$$
よって、
$$
R_G^2 = \dfrac{\dfrac{4\pi}{5} R^5 \rho_0}{\dfrac{4\pi}{3}R^3 \rho_0} = \dfrac{3}{5} R^2
$$
$$
\therefore \;\;\;\;\; R_G = \sqrt{\dfrac{3}{5}} R \;\;\;\;\;\; (答)
$$
図3と図4に、球の散乱関数を示しました。

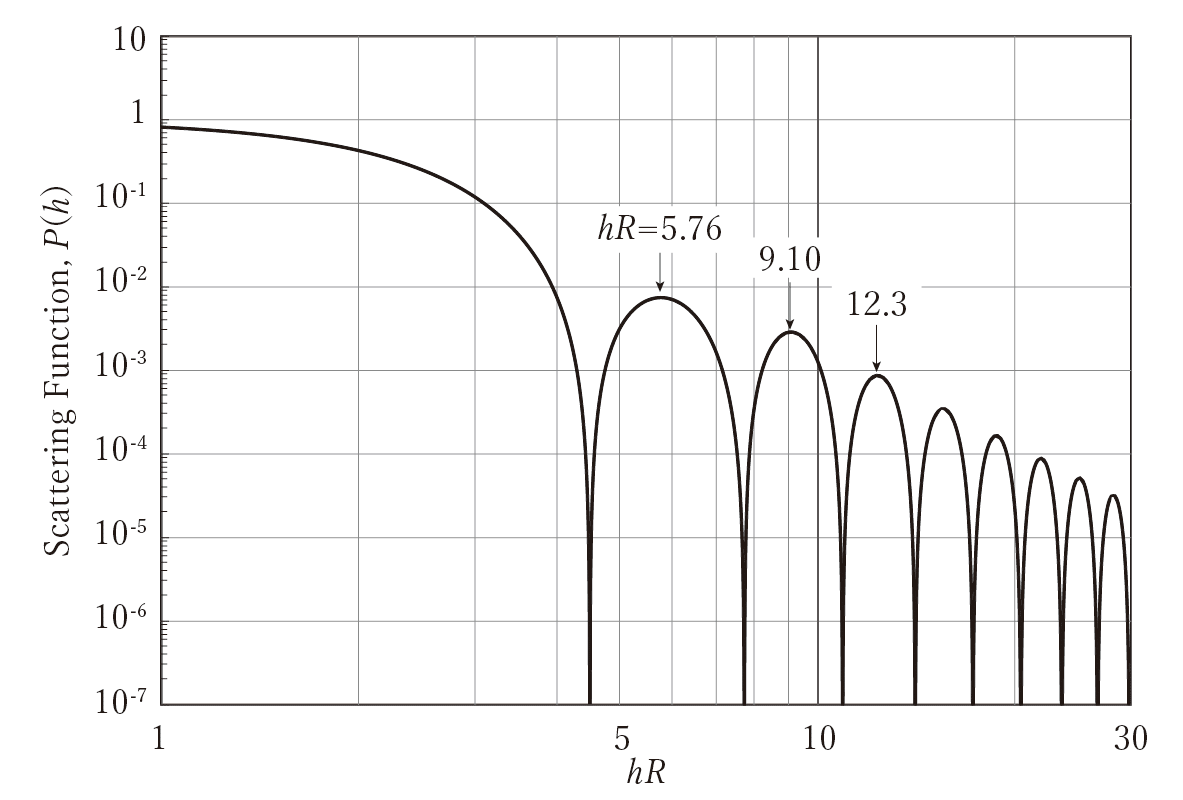
(終)
文献
[1] 小角X線散乱(SAXS)(1) - 基本的なこと(note記事)
[2] 小角X線散乱(SAXS)(5)- 座標系と体積要素(体積素片)dr(note記事)
[3] 部分積分です:
$$
\int f(x)g'(x) \mathrm{d}x = f(x)g(x) - \int f'(x)g(x) \mathrm{d}x
$$
$${f(x)=x}$$、$${g(x)=\cos x}$$にします。
[4] $${O(x^n)}$$は、$${x}$$の$${n}$$以上の次数の項が続くという意味です。$${x \ll 1}$$のときは次数が増えるに従って無視できるほど小さくなると予想されます。代わりに、$${\cdots}$$と記されていることもあります。ちなみに、$${O}$$はランダウの記号と呼ばれています。
[5] 森口繁一、宇田川銈久、一松信、数学公式Ⅱ(岩波全書)、岩波書店、1957.
$$
\ln (1-x) = -\displaystyle\sum_{n=1}^\infty \dfrac{x^n}{n} = -x - \dfrac{x^2}{2} - \cdots \;\;\;\;\;\; [|x| \leq 1, x\neq1]
$$
[6] 橋本竹治、"X線・光・中性子散乱の原理と応用"、講談社、2017. 大著です。原理的なことが詳細に、しかも網羅的に著されています。
様々な形状の散乱関数(形状因子、干渉因子)
【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。
