確率分布を活用した自動売買:価格変動の分布を予測するFX自動売買ツールの開発
FXの価格変動は、確率分布に従うと一般的に考えられています。特に、極端な値動きやファットテール(分布の裾が厚い現象)が特徴的な市場では、単純な正規分布では不十分で、より複雑な分布が適用されることが多く見られます。一方、GOLDの価格変動については、リターン(価格変動率)がt分布に従う傾向があるとされており、この特性を利用することでボラティリティや異常値を適切にモデル化できる可能性が指摘されています。
本記事では、これらの確率分布を用いて価格変動をモデル化し、その結果を基に取引戦略を構築する自動売買ツール「GSD-EA」を紹介します。「GSD-EA」は、グリッドサーチを活用して分布パラメータを推定する仕組みを備え、価格変動の予測に基づく精密なトレードを可能にします。
さらに、記事の最後では「GSD-EA」のソースコード全文を公開し、実際に使用可能な状態で提供します。確率分布を活用した自動売買の基礎から応用までを解説する本記事を通じて、分布解析を取り入れた新しい取引手法を体感してください。
確率分布を用いた取引戦略
まずは、以下のグラフをご覧ください。
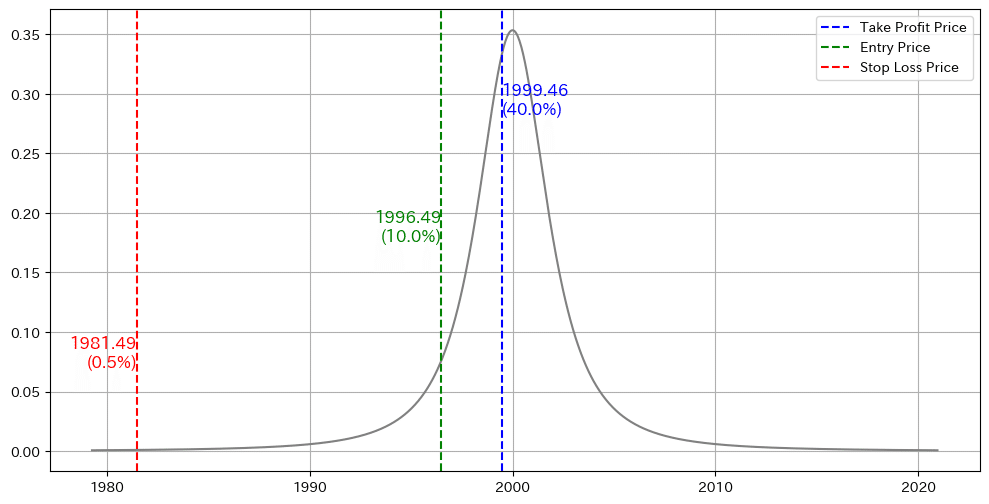
このグラフは、t分布に基づく価格変動をモデル化し、それを活用した取引戦略の一例を示しています。
取引条件の設定
本戦略では、以下の条件に基づきエントリーや利確、損切りを行います。
エントリーポイント(Entry Price):1996.49(分位点の10%)
利確ポイント(Take Profit Price):1999.46(分位点の40%)
損切りポイント(Stop Loss Price):1981.49(分位点の0.5%)
本記事の目標は、確率分布を活用した自動売買戦略を構築することです。
これらの設定により、価格変動がt分布に従うという仮定の下で、損益を確率論的に管理する戦略の実現を目指します。
今後の検証
この戦略の有効性を確認するため、価格データを使用した反復的な取引シミュレーションを行います。これにより、取引戦略の妥当性とパフォーマンスを詳細に検証していきます。
サンプルデータの生成
まずは、サンプルデータを作成してみましょう。ただし、ここで作成するのは単なるランダムな価格変動データではありません。特定の条件を意図的にコントロールしたt分布に基づく価格変動データを生成します。
サンプルデータを作る意味とは?
なぜサンプルデータの作成が必要なのでしょうか?今回の試みでは、「確率分布を正確に予測できれば、取引戦略のパフォーマンスが向上する」という仮定を検証します。
しかし、たとえ分布予測が完璧であっても、それが実際に利益を生み出さないのであれば、戦略としての意味はありません。
だからこそ、まず「分布を把握できている環境で、確実に利益を生み出せる戦略」を構築することが重要なのです。この基盤があれば、次に実際の市場データに適用する際は分布推定に注力するだけで良くなります。
サンプルデータ生成のプロセス
今回作成するサンプルデータの目的は、「実際のGOLD市場で起こり得る価格変動を模倣すること」にあります。このため、t分布を基に価格変動モデルを設計しました。以下、その詳細をご説明します。
1. t分布と主要パラメータ
価格変動の生成には、極端な価格変動が発生しやすいという特徴を持つt分布を採用しました。GOLDの価格データを模倣する際に適しているためです。今回使用したt分布の主要なパラメータは以下の通りです:
自由度 (ν): 1.99
自由度が低いほど、分布の裾が厚くなり、極端な価格変動が発生しやすくなります。今回の設定では、自由度1.99で市場の変動特性を反映させています。リターンのスケール (σ): 0.000170
これは価格変動のスケールを示す値で、小さいほど細かな変動を再現できます。
これらのパラメータを用いてリターン(価格変動幅)を生成し、それを累積することで各時点の価格を計算します。また、実際のGOLDの価格を意識して、価格が特定の範囲(1500~2500)を超えないよう調整しています。
標準偏差 (σ) と時間スケールの関係
価格データの標準偏差は、観測される時間スケールによって変化します。この関係について説明します。
短時間スケールでの標準偏差
30秒単位で観測される価格変動の標準偏差は、σ = 0.000170です。短い時間スケールでは、個々の変動が小さくなります。
長時間スケールでの標準偏差
一方、4時間単位で観測される場合、累積的な価格変動により標準偏差は大きくなり、σ = 0.000929になります。
3. 計算例
標準偏差のスケール変化は次のように計算されます。
σT = 0.000170 × √(14400/30) ≈ 0.000929
この結果から、30秒単位の標準偏差 0.000170 が、4時間(14400秒)単位では 0.000929 に対応することが確認できます。
データの生成
データは、30秒間隔のティックデータとして生成することにします。
売値と買値の差(スプレッド)の追加
実際の市場を模倣するため、売値と買値の価格差(スプレッド)をランダムに生成します。このスプレッドは、平均値0.2、標準偏差0.05の正規分布に基づく設定にしました。それを使い、各時点で以下の価格を算出します。
bid価格(売値): 中心価格からスプレッドの半分を引いた値。
ask価格(買値): 中心価格にスプレッドの半分を足した値。
データセットの構築
最終的に、以下の要素を含むデータを表形式(データフレーム)にまとめます。
各ティックの時間
bid価格(売値)
ask価格(買値)
スプレッド値
このデータセットは、「t分布の特性を前提にしたGOLD価格データ」を模倣したものです。このデータを用いて、次に取引戦略のパフォーマンスを検証していきます。
t分布に基づいた取引戦略
t分布の確率密度関数
確率密度関数 (Probability Density Function) は、特定の値が現れる確率を表す曲線です。t分布の確率密度関数は、以下のパラメータによって形状が決まります:
平均値 (μ): 2,000
自由度 (ν): 1.99
標準偏差 (σ): 0.000929

t分布の特徴として、正規分布に似ていますが尾が重く、極端な値動きが発生する確率を反映します。自由度が大きいほど正規分布に近づきます。
分位点の意味と活用

分位点は累積確率が特定の値となるポイントを示し、次のように捉えます。
10%分位点: 観測値が1996.49以下である確率が10%
50%分位点(中央値): 価格の平均である2000.00
90%分位点: 観測値が2003.51を超える確率が10%
具体的な取引パターンの紹介
今回のt分布の分位点を活用した取引戦略を改めて振り返ります。

平均値 (μ): 2,000、自由度 (ν): 1.99、標準偏差 (σ): 0.000929というパラメータの場合は、上記のグラフのように、
エントリーポイント(Entry Price):1996.49
利確ポイント(Take Profit Price):1999.46
損切りポイント(Stop Loss Price):1981.49
となります。
以下、インプットデータからt分布のパラメータを推定した上で、エントリーポイント、利確ポイント、損切りポイントの3つを設定して取引シミュレーションを行う例をご紹介します。
サンプル1( 利確パターン)
エントリーポイント(Entry Price):1996.28
利確ポイント(Take Profit Price):2000.53
損切りポイント(Stop Loss Price):1976.83

価格がエントリーポイントである1996.28を下回ったタイミングで買いエントリー、その後損切りポイントである1976.83まで下がることなく、2000.53まで価格が上昇したため、ポジションを利益確定します。
サンプル2(損切りパターン)
エントリーポイント(Entry Price):1995.68
利確ポイント(Take Profit Price):1997.51
損切りポイント(Stop Loss Price):1987.32

価格がエントリーポイントである1995.68を下回ったタイミングで買いエントリー、その後損切りポイントである1987.32まで価格が下がってしまったため、損失確定でポジションをクローズです。
サンプル3(時間制限クローズ)
エントリーポイント(Entry Price):1995.81
利確ポイント(Take Profit Price):2000.55
損切りポイント(Stop Loss Price):1974.49

価格がエントリーポイントである1995.81を下回ったタイミングで買いエントリーしましたが、その後利確ポイントである2000.55にも、損切りポイントである1974.49にも到達することなく4時間が経過したため、ポジションの時間制限(Time Limit)を超過ということでその時点の価格でクローズです。
サンプル4(エントリーなし)
エントリーポイント(Entry Price):1996.37
利確ポイント(Take Profit Price):1999.56
損切りポイント(Stop Loss Price):1980.78
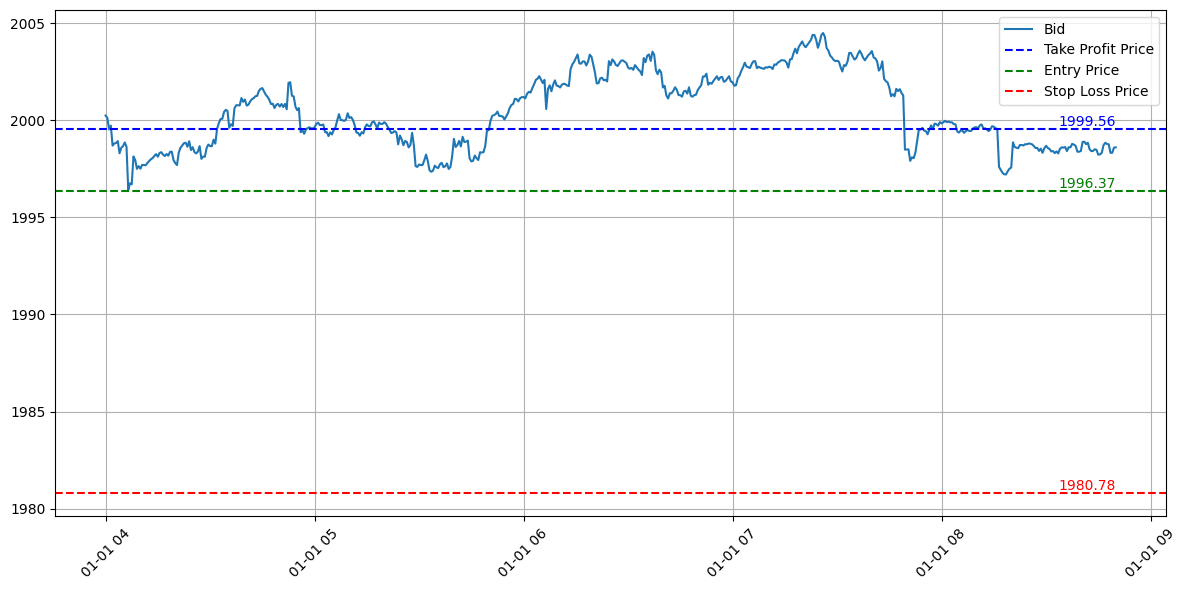
エントリーポイントは1996.37でしたが、エントリーの制限時間である4時間の間にそこまで価格が下落することなかったため、エントリーなしで試行を終えます。
取引シミュレーション
さて、以上の取引戦略で、ランダムで価格データの生成と取引シミュレーションを1,000回繰り返し、結果を集計してみます。
検証1(理想的な条件下でのパフォーマンス確認)
まずは、取引戦略に用いるt分布とパラメータに従う価格データを生成して、理想的な環境(将来の価格変動の確率分布が正確に予測できている状態)を整えて検証してみます。
シミュレーション結果
試行回数: 1,000回
エントリー数: 578回(エントリー率: 57.80%)
勝利数: 578回(勝率: 100.00%)
総損益: 228,586円 (総利益: 228,586円 総損失: 0円)

この結果を整理すると以下の通りです。

想定したt分布に従う価格データを30秒単位で生成
平均価格(スタート価格)を2000とし、4時間以内にエントリー価格(1996.49)まで価格が下落した割合が1,000回のうち578回(エントリー率57.8%)
エントリー価格(1996.49)に達した後4時間以内に、損切価格(1981.49)に到達する前に利確目標(1999.46)に到達した割合が、エントリーした578回のうち578回(勝率100%)
勝率100%という結果は出来過ぎですが、想定通りの価格データを用意したので当然といえば当然です。
ただし、ここで重要なのは、
「確率分布(のパラメータ)を正確に予測することさえできれば、この取引戦略は有効に機能する」
ということが一定程度示されたことです。
したがって、あとは分布の予測精度を高めることに注力するだけで損益という結果は勝手に付いてくる、つまり、分布の予測精度を高めることが損益パフォーマンスの向上に直結する状態が整ったことになります。
いくら分布の予測精度を高めたところで、それを活かせる有効な取引戦略が存在しなければその努力は水の泡になりますので、実践を意識した取り組みを行う場合には、とても重要なポイントです。
検証2(実データを用いた精度確認)
それでは、実際の価格データを用いて検証してみます。今回使用するのは、GOLD(XAU/USD)の約2年分(2023年1月〜2024年10月)のティックデータです。


ティック(Tick)とは、金融商品における価格変化の最小単位(呼び値)を指し、変動の都度を意味します。ティックデータの具体的な取得方法は以下の記事等を参考にしてください。
リアルデータを用いた検証方法
この実際のtickデータを用いて、以下の手順で検証してみます。
2年分のtickデータからランダムで24時間分のデータを抽出
このデータのうち最初の4時間分のデータからt分布のパラメータを推定(分布の推定には最尤法を用いる)
推定したt分布から、エントリーポイント、利確ポイント、損切りポイントを設定して取引シミュレーションを1,000回繰り返す
シミュレーション結果
試行回数: 1,000回
エントリー数: 411回(エントリー率: 41.10%)
勝利数: 355回(勝率: 86.37%)
総損益: 157,425円 (総利益: 178,316円 総損失: 20,891円)
プロフィットファクター: 8.54
リカバリーファクター: 32.75(最大ドローダウン: 4,807円)

これは、実際のデータを用いているのですが、24時間分のデータの最初の4時間で分布のパラメータを推定しています。その上で、その最初の4時間分に対して取引シミュレーションを行っています。
つまり、将来の価格データを知っている状態で取引を行うというあまり現実的ではない状態になるので、結果が良好になるのは想定内です。
最尤法によるt分布のパラメータ推定、そしてその分布を前提とした取引戦略がある程度機能することが確認できたことになります。
言い換えれば、この検証でも、
「確率分布(のパラメータ)を正確に予測することさえできれば、この取引戦略は有効に機能する」
ということを確かめています。
検証3(現実的な環境でのシミュレーション)
続いて、より現実的なトレード環境を想定して以下の検証を行います。
より現実的なトレードシミュレーション
2年分のtickデータからランダムで28時間分のデータを抽出
このうち最初の4時間分のデータから最尤法でt分布のパラメータを推定
最初の4時間分を除いた後半の24時間分を取引シミュレーションに使用
これまでの検証と同様にシミュレーションを1,000回繰り返す
検証2との違いは、分布のパラメータを推定するのは、トレード開始時点で把握可能な過去4時間分のデータにしたことです。実際のトレードにおいても入手可能な過去データから、将来の分布を予測するという条件に変更しました。
シミュレーション結果
試行回数: 1,000回
エントリー数: 317回(エントリー率: 31.70%)
勝利数: 207回(勝率: 65.30%)
総損益: 32,443円 (総利益: 77,478円 総損失: 45,035円)
プロフィットファクター: 1.72
リカバリーファクター: 4.05(最大ドローダウン: 8,010円)

検証2では勝率86.37%だったのに対し、勝率が65.30%になりました。プロフィットファクターも8.54から1.72と、パフォーマンスが下がってきました。つまり、あとは予測の精度をさらに高めることができれば、より良好なパフォーマンスを実現することができるであろうというところです。
MT5用EAの作成方法
さて、それでは以上のロジックをFX自動売買ツールに取り込んで、MT5用のEAを作成してみます。
まず、これまでの検証ではPython のscipy.statsというライブラリを用いて最尤法によってt分布のパラメータを推定していました。これはEAを作成するMQL5では簡単に実装しづらいため、グリッドサーチで近似的に再現します。
最尤法(Maximum Likelihood Estimation: MLE)
概要
最尤法とは、観測データから最も「それっぽい」分布を見つけるための方法です。具体的には、データが実際に起こる確率を最大にする分布のパラメータを探します。
データに合った分布を選び、そのパラメータ(平均値や標準偏差など)を決めます。
計算では「このパラメータならデータがどれくらい起こりやすいか」を比較します。
最もデータに合ったパラメータを見つけることで、将来の予測に活用します。
特徴
明確な理論に基づく手法: データを元にしているため、信頼性が高いです。
一意の解が得られることが多い: 一部の状況を除いて、答えがはっきりと決まります。
数値計算が必要: 複雑な場合はコンピュータで試行錯誤を繰り返して計算します。
グリッドサーチ(Grid Search)
概要
グリッドサーチは、最尤法とは少し違い、「試してみて決める」方法です。あらかじめパラメータの候補をいくつか設定し、それらを一つずつ試してみて、最も良い結果を選びます。
例えば、平均値が1990、2000、2010の場合をそれぞれ計算して、どれがデータに合うかを探します。
計算は簡単で、すべてのパターンを調べるだけです。
特徴
シンプルで直感的: 難しい計算がいらず、手順が分かりやすいです。
パラメータの範囲を設定する必要がある: 試す候補を最初に決める必要があります。
計算コストが増える: 候補が多いほど、計算時間が長くなるのが難点です。
取引シミュレーション
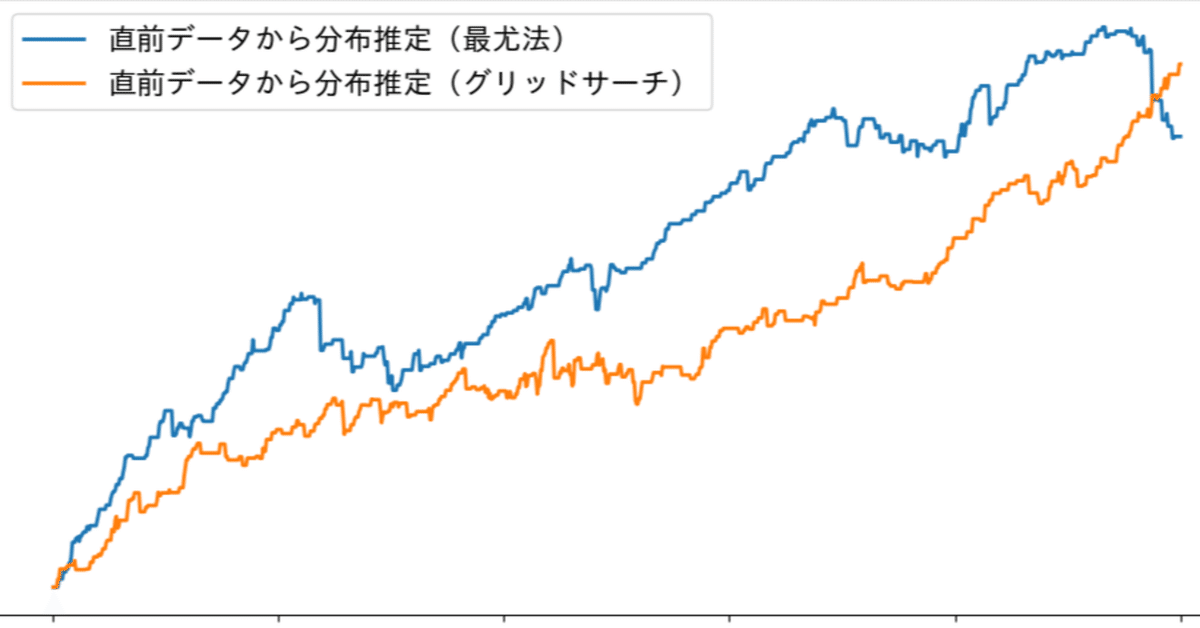
それでは、先ほどの検証3(リアルシミュレーション)と同じ条件でPyhotnにおける分布予測を最尤法からグリッドサーチに変更して、結果を比較してみます。
シミュレーション結果
試行回数: 1,000回
エントリー数: 320回(エントリー率: 32.00%)
勝利数: 193回(勝率: 60.31%)
総損益: 37,655円 (総利益: 79,245円 総損失: 41,590円)
プロフィットファクター: 1.91
リカバリーファクター: 8.23(最大ドローダウン: 4,573円)
最尤法による分布推定と完全に一致するわけではありませんが、結果を比較するとグリッドサーチによる方法である程度再現できていることが確認できました。
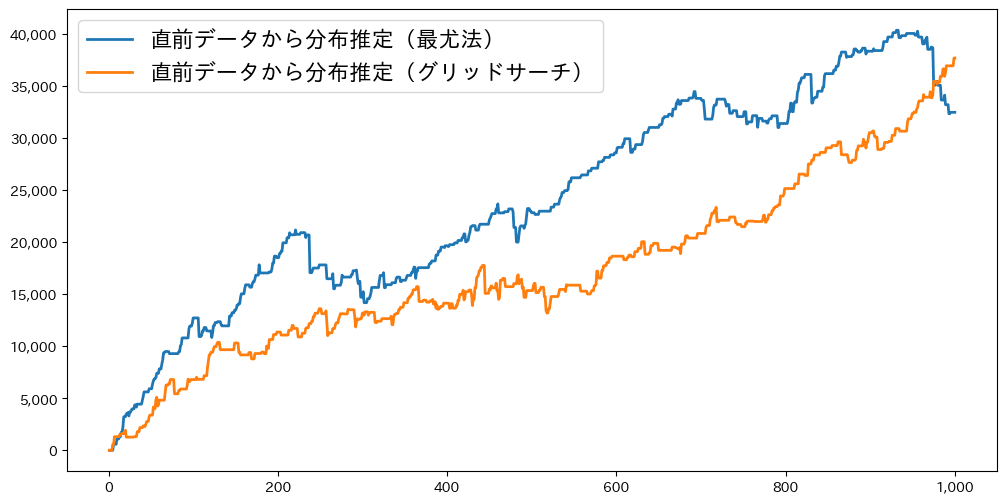
続いて、これをMT5用EAとしてロジック実装してみようと思います。
GSD-EA(MT5用)の開発
今回開発した「GSD-EA」は、Grid Search Distribution(グリッドサーチ分布)の略です。FXやGOLDの価格変動を効率的に利用するための自動売買プログラム(EA: Expert Advisor)です。このEAは、グリッドサーチを活用して価格変動データから最適な確率分布(t分布)のパラメータを推定し、それを基に取引戦略を構築する仕組みを持っています。
EAロジックの概要
以下に、ロジックのポイントを解説します。
1. 価格データを分析
EAは、1分足の終値データを取得し、そのデータを基に価格変動のパターンを分析します。具体的には、過去240本(4時間分)の終値データを使い、以下の処理を行います。
対数リターンの計算: 価格変動率を計算して、価格の変動パターンを把握。
t分布パラメータの推定: 価格変動がt分布に従うと仮定し、最適な分布パラメータ(自由度、スケールなど)を算出。
2. エントリーと目標価格の決定
t分布のパラメータを基に、次のような価格を計算します。
エントリーポイント: エントリーするための目安価格。
利確ポイント(TP): 利益確定のための目標価格。
損切りポイント(SL): 損失を限定するための価格。
EAはこれらの価格を計算し、現在の市場価格がエントリーポイントに達した場合に取引を開始します。
3. 自動取引の流れ
このEAは、以下のルールに従って取引を管理します:
条件の確認:
現在の価格がエントリーポイントを満たしているか?
スプレッド(売値と買値の差)が許容範囲内か?
エントリー:
条件を満たした場合、買いまたは売りのポジションを自動でオープン。
ポジション管理:
価格が利確ポイントや損切りポイントに達した場合、ポジションを自動でクローズ。
また、エントリーしてから4時間を超えた場合もポジションをその時点の価格でクローズ。
インプット設定
以下に、インプット部分の内容と設定方法を解説します。

ロット数
初期設定: 0.01
説明: 1回の取引で使用するロット数を指定します。
入力例: 0.05(取引量を増やす場合)
スリッページ
初期設定: 10
説明: 許容するスリッページ(価格変動による注文価格と約定価格のずれ)の範囲を指定します。ポイント単位で設定します。
入力例: 5(スリッページを厳しく制限する場合)
許容スプレッド
初期設定: 30
説明: スプレッド(売値と買値の差)がこの値を超える場合は取引を行いません。ポイント単位で設定します。
入力例: 20(スプレッドがより狭いタイミングのみで取引する場合)
マジックナンバー
初期設定: 10001
説明: このEAが管理するポジションを識別するための固有番号です。複数のEAを同時に使用する場合、この番号をユニークにすることで干渉を防ぎます。
入力例: 20002(異なるEAと混在させる場合)
1:buy, 2:sell, 3:buy&sell(取引モード)
初期設定: 1
説明: 取引の種類を指定します。
1: 買いエントリーのみ
2: 売りエントリーのみ
3: 買い・売り両方をエントリー
入力例: 3(買い・売り両方を取引する場合)
バックテスト結果
初期設定でバックテストを行った結果は以下の通りです。

損益グラフ

事前にPythonでシミュレーション比較してみると以下の通りです。
Pythonシミュレーション
勝率: 60.31%、プロフィットファクター: 1.91、リカバリーファクター: 8.23
MT5バックテスト
勝率: 65.65%、プロフィットファクター: 1.09、リカバリーファクター: 1.20
Pythonシミュレーションの場合は、ランダムで28時間分のデータを抽出して取引シミュレーションを行うことを1,000回繰り返すという方法でした。
一方で、MT5バックテストでは、2023年1月から順番に取引機会を確認し、一度ポジションを持ったらその後ポジションをクローズするまで次のエントリーは行いません。
したがって、全く同じ条件ではないため単純な比較は難しいですが、概ね同等のロジックを構築することはひとまずできたようです。
さらなる精度向上へ
今回のEA「GSD-EA」では、グリッドサーチを用いて分布パラメータを推定する方法を採用しました。この手法はシンプルで計算効率が高く、FXやGOLD市場の特徴を適切にモデル化するのに有用です。しかし、さらなる精度向上を目指す場合、他にもさまざまな分布推定のアプローチが考えられます。
Pythonの最尤法をEAにも取り入れる
MQL5ではPythonのライブラリでscipy.statsをそのまま使用することが難しいため、今回はグリッドサーチを用いて近似的に分布を推定しました。しかし、PythonとMQL5を連携させることで、最尤法(Maximum Likelihood Estimation; MLE)をEAに取り入れることが可能です。
最尤法を利用すれば、分布パラメータをより正確に推定でき、より精密な取引戦略の構築が期待できます。このアプローチを実現するFX自動売買ツール「MLD-EA」(Maximum Likelihood Distribution-EA)の開発については、以下の記事で詳しく解説しています。
マルコフ連鎖モンテカルロ法の導入
もう一つ、さらなる精度向上を目指したアプローチとして、マルコフ連鎖モンテカルロ法(MCMC: Markov Chain Monte Carlo)を用いた分布推定が挙げられます。MCMCは、複雑な分布の推定や、事後分布の形状をモンテカルロサンプリングを通じて効率的に求める方法です。この手法を取り入れることで、以下のようなメリットが得られます:
複雑な分布の推定: t分布に限らず、より複雑な分布の特性を把握可能。
パラメータの不確実性の定量化: 分布のパラメータ推定値に加え、その信頼区間やばらつきも得られる。
高度なリスク管理: 価格変動の不確実性をより正確に反映した取引戦略の設計が可能。
特に、StanやPyMCなどのPythonライブラリを活用することで、MCMCを実用化する道が開かれます。この手法は、グリッドサーチや最尤法に比べて計算量が多いですが、高精度の分布推定が必要な場合に有効です。
当記事の検証3(現実的な環境でのシミュレーション)において、MCMC(マルコフ連鎖モンテカルロ法)を採用した場合の結果も簡単にご紹介しておきます。

グラフからは、この3つの中ではMCMCが最も安定的なパフォーマンスを出せているように見えますので、精度向上に期待できます。
マルコフ連鎖モンテカルロ法(MCMC: Markov Chain Monte Carlo)を実装したEAの作成方法については、以下の記事にて詳しく解説しています。
有料部分の内容
有料部分にて、この記事でご紹介した「GSD-EA」(Grid Search Distribution-EA)をのソースコード全文を掲載したmq5ファイル(MetaTrader5向けに書かれたプログラム)をダウンロード可能にしておきます。
そのままコンパイルするだけでも、GSD-EA_note.ex5が作成可能ですので、プログラムがよくわからない方でもEAとしてそのまま利用可能です。
EAの作成方法や使い方についての具体的な手順は以下の記事を参考にしてください。
注意点
記事執筆時点で稼働確認を行なっており、エラーが出ないことを確認しておりますが、その後の環境変化等で想定通りに稼働しない可能性はございます。動作保証等はいたしかねますのでご了承ください。
リアル口座にアクセスして取引を行うことも可能なコードになっておりますが、必ずデモ口座で事前に稼働確認をしていただくことを推奨いたします。
当記事で解説しているロジック通りの動作を保証するものではございません。あくまでFX自動売買ツール開発のためのサンプルコードとしてご活用ください。
当記事の有料部分からダウンロード可能なのはグリッドサーチによる簡易的な分布推定方法を採用したバージョンのみであり、最尤法やマルコフ連鎖モンテカルロ法(MCMC法)を搭載したバージョンは別記事になります。
最尤法による分布推定(MLD-EA)
マルコフ連鎖モンテカルロ法による分布推定(MCMC-EA)
mq5ファイルのダウンロード
ここから先は
¥ 5,000
Amazonギフトカード5,000円分が当たる
よろしければ応援お願いします。いただいたチップは今後の記事の執筆に活用させていただきます。
