t分布をベースにしたベイズ推定型FX自動売買ツール（MCMC-EA）の開発

前回の記事では、最尤法（MLE: Maximum Likelihood Estimation）を用いてt分布のパラメータを推定し、FX自動売買を行う「MLD-EA（Maximum Likelihood Distribution-EA）」をご紹介しました。

そこで取り上げたのは、PythonとMQL5を連携させて最尤法を活用することで、確率分布のパラメータ推定の精度を向上させる方法です。

今回は、そのMLD-EAをさらに進化させ、分布のパラメータ推定部分にマルコフ連鎖モンテカルロ法（MCMC: Markov Chain Monte Carlo）を導入したFX自動売買ツール（MCMC-EA）を開発します。MCMCを使用することで、最尤法よりも柔軟で詳細な分布推定が可能となり、さらなる予測制度の向上が期待できるはずです。

概要

この記事では、以下の内容を中心に解説します。

1. MCMCを用いた分布推定の利点と最尤法との違い

2. MCMC-EAとMLD-EAの損益シミュレーション結果の比較

3. MLD-EAからMCMC-EAにバージョンアップする方法

ベイズ推定とは？

MCMCを用いた分布推定は、ベイズ推定の枠組みの中で行われます。ベイズ推定では、「事前分布 × 尤度 = 事後分布」というベイズの定理を用いて、観測データをもとに確率分布を更新します。MCMCは、この事後分布を近似的に求めるためのアルゴリズムであり、t分布のような複雑な分布のパラメータ推定にも適しています。

もう少し一般的なベイズ推定（ベイズ統計）については以下の記事も参考にしてください。

この記事では、最尤法（MLE）とマルコフ連鎖モンテカルロ法（MCMC）の違いや利点に触れながら、ベイズ推定を活用したMCMC-EAの作成方法をご紹介します。

MLD-EAの構造

前回の最尤法を用いたEA（MLD-EA）においては、以下のような構造でMQL5とPythonの連携を実現させていました。

MQL5とPythonの連携

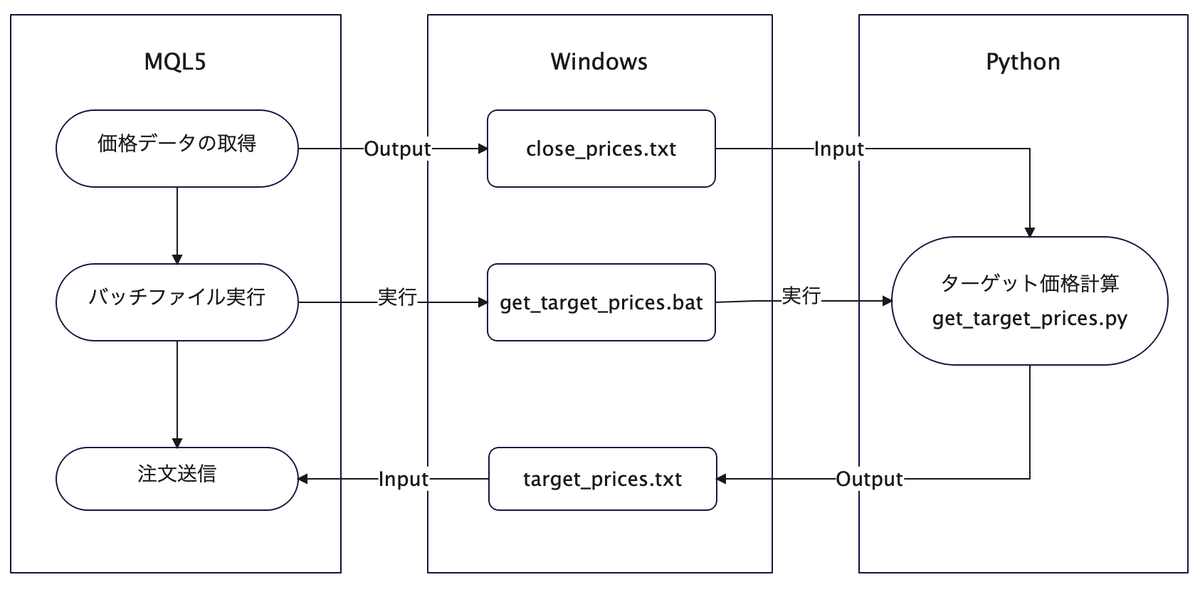
この中で、t分布のパラメータ推定とターゲット価格計算は全てPythonスクリプト（get_target_prices.py）の中で行なっています。
この分布のパラメータ推定方法について、最尤法からマルコフ連鎖モンテカルロ法へ発展させることが今回の目的ですので、MQL5のロジックは全く変えずに、Pythonのコードを変更するだけでバージョンアップが可能です。

損益シミュレーション結果

先に、MLD-EAをMCMC-EAにバージョンアップした場合のパフォーマンス比較結果をご紹介します。

シミュレーション方法

• 2年分のGOLDの価格データからランダムで28時間分のデータを抽出

• このうち最初の4時間分のデータから最尤法でt分布のパラメータを推定

• 最初の4時間分を除いた後半の24時間分を取引シミュレーションに使用

• 上記の方法でシミュレーションを1,000回繰り返す

この方法は、以下の記事における検証3（現実的な環境でのシミュレーション）と同様です。詳しい前提については、この記事もあわせてご確認ください。

詳細な結果はそれぞれ以下の通りです。

シミュレーション結果（最尤法）

試行回数: 1,000回
エントリー数: 317回（エントリー率: 31.70%）
勝利数: 207回（勝率: 65.30%）
総損益: 32,443円 （総利益: 77,478円 総損失: 45,035円）
プロフィットファクター: 1.72
リカバリーファクター: 4.05（最大ドローダウン: 8,010円）

シミュレーション結果（MCMC）

試行回数: 1,000回
エントリー数: 323回（エントリー率: 32.30%）
勝利数: 220回（勝率: 68.11%）
総損益: 54,200円 （総利益: 81,575円 総損失: 27,375円）
プロフィットファクター: 2.98
リカバリーファクター: 16.66（最大ドローダウン: 3,254円）

損益グラフ（最尤法 vs MCMC）

それぞれの結果を損益グラフで重ねてみます。

最尤法 vs MCMC

最尤法と比較すると、MCMCの方が一貫して安定的なパフォーマンスを発揮していることが見受けられます。MCMCを使用することで、最尤法と比較して予測制度の向上した可能性も高いと判断できます。

MLD-EAにおけるPythonの処理

ここで改めて、MLD-EAにおけるPythonの処理について説明します。

ターゲット価格の計算

• MQL5から出力された240本（4時間分）の1分足終値データから、t分布のパラメータを推定

• 推定したt分布の分位点を基準としてターゲット価格を計算

• 計算したターゲット価格をテキストファイル（target_prices.txt）で出力

最終的には、例えばbuy注文の場合は以下のようなターゲット価格を出力します。

buy注文のターゲット価格

例えば、推定されたt分布のパラメータが平均値 (μ): 2,000、自由度 (ν): 1.99、標準偏差 (σ): 0.000929だった場合は、上記のグラフのように、

• エントリー価格（Entry Price）：1996.49

• 利確価格（Take Profit Price）：1999.46

• ロスカット価格（Stop Loss Price）：1981.49

というターゲット価格が計算されます。

t分布のパラメータ推定（MLEによる推定）

以下は、最尤法（MLE）を用いてt分布のパラメータを推定するコードです。

mle_nu, mle_loc, mle_scale = t.fit(log_returns)

• 何をしているか:
  PythonのScipyというライブラリのt.fit関数を使って、対数リターンが従うt分布の3つのパラメータ（自由度ν、位置loc、スケールscale）を最尤法で推定しています。

• パラメータの意味:

  • ν（自由度）: データのばらつきの度合いを決定し、値が小さいほど「裾が厚い分布」となります。

  • loc（位置パラメータ）: データの中心（平均値）を示します。

  • scale（スケールパラメータ）: データの広がり（ボラティリティ）を示します。

• 最尤法の役割:

  • 最尤法（MLE）は観測データから「最も確からしい」パラメータを計算する手法であり、t分布の近似値を算出しています。

MLD-EAからMCMC-EAへの拡張

それでは、MLD-EAをMCMC-EAに拡張する方法を具体的に説明していきます。ここでは、以下の記事においてダウンロード可能なMLD-EA用のPythonスクリプト「get_target_prices.py」をベースにします。

ライブラリのインポートの追加

「get_target_prices.py」の冒頭には、以下の通り、いくつかのライブラリをインポートするコードが記載されています。

MLD-EA

import pandas as pd
import numpy as np
from scipy.stats import t
from datetime import datetime

これの最後に、「import pymc as pm」というコードを追加します。MCMCではpymcというライブラリを使用するためです。

MCMC-EA

import pandas as pd
import numpy as np
from scipy.stats import t
from datetime import datetime
import pymc as pm

ターゲット価格計算方法の変更

続いて、実際にターゲット価格を計算するためのコードを拡張します。

MLD-EA

# ターゲット価格を計算
target_prices = calculate_prices(mu_price, mle_nu, mle_scale * 10)
print(mle_nu, mu_price, mle_scale)

上記のターゲット価格を計算する部分について、以下のコードに置き換えます。

MCMC-EA

# pymcモデルの定義
with pm.Model() as model:
    # 最尤法による推定値を事前分布に設定
    sigma = pm.HalfNormal('sigma', sigma=mle_scale)

    # 観測モデル
    returns = pm.StudentT('returns', nu=mle_nu, mu=mle_loc, sigma=sigma, observed=log_returns)

    # MCMCサンプリング
    trace = pm.sample(2000, return_inferencedata=True, progressbar=False, target_accept=0.95)

# 事後分布のサマリーを取得
summary = trace.posterior.mean(dim=("chain", "draw"))

# 予測σを取得
estimated_sigma = summary['sigma'].values.item()  

# ターゲット価格を計算
target_prices = calculate_prices(mu_price, mle_nu, estimated_sigma * 10)
print(mle_nu, mu_price, estimated_sigma)

以上の変更を行うだけで、MCMCの追加処理は完了です。

拡張したMCMC処理の概要

このコードは、初期推定として最尤法を採用しつつ、さらにMCMC（マルコフ連鎖モンテカルロ法）でパラメータ推定の精度を高めています。

1. 最尤法の活用: 初期推定として、t分布のパラメータを最尤法で推定

2. ベイズ推定の導入: 最尤法の推定結果を事前分布として用い、MCMCによって分布パラメータ（ここではσのみ）を事後分布推定

pymcモデルの構築

• 事前分布:
  sigmaには、最尤法（MLE）で得られたパラメータ（mle_scale）を基にした半正規分布を設定しています。この事前分布は、MCMCが探索を行うスタート地点を意味しています。

• 観測モデル:
  returnsは観測された対数リターンを表し、t分布のパラメータとして最尤法（MLE）で得られたmle_nu（自由度）やmle_loc（位置パラメータ）を使用しています。

MCMCサンプリング

pm.sampleによって、事後分布を近似的にサンプリングします。この過程で、観測データに基づいたt分布パラメータの更新が行われます。

パラメータ推定結果の比較

それぞれの分布推定を実施すると、例えば以下のような結果が得られます。

MLD-EAのパラメータ推定結果

1.9825544848905752 2709.5486350789056 0.00017507828036830692

• 1.9825544848905752: 自由度（ν）

• 2709.5486350789056: 基準価格（μ）

• 0.00017507828036830692: スケール（σ）

MCMC-EAのパラメータ推定結果

1.9825544848905752 2709.5486350789056 0.00017544149707520796

• 1.9825544848905752: 自由度（ν）

• 2709.5486350789056: 基準価格（μ）

• 0.00017544149707520796: スケール（σ）

パラメータ推定結果比較

どちらも似たような結果が出ているように見えますが、以下の通りスケール（σ）が微妙に異なっています。

• 0.00017507828036830692: スケール（最尤法）

• 0.00017544149707520796: スケール（MCMC）

自由度（ν）と基準価格（μ）はMLD-EAとMCMC-EAで同じ結果を使う仕組みにしているので全く一致します。このスケール（σ）の微妙な差が、ターゲット価格に影響し、先ほどの損益パフォーマンスの差を生んだと考えられます。

実行時のWARNING（警告）について

MCMC-EAを実際に動かすためには、適切なPythonの環境設定になります。特にpymcのインストールにつまずく方も多いかもしれません。
ただし、ある程度の環境が整っていれば、例えば以下のようなWARNING（警告）が出たとしても、実際のEAを使用する上ではそこまで問題になりません。

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [sigma]
Sampling 2 chains for 1_000 tune and 2_000 draw iterations (2_000 + 4_000 draws total) took 4 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
1.9825544848905752 2709.5486350789056 0.00017544149707520796
続行するには何かキーを押してください . . .

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

• この警告は、計算を高速化するために使われる「BLAS」というライブラリが適切に設定されていないことを示しています。

• 代わりにNumPyの標準的な計算方法が使われています。

• 計算は動作しますが、速度が遅くなる可能性があります。

以下、ひとまず上記の状態（最低限MCMC-EAを動かせる状態）にするための初心者向けの簡単な設定手順を詳しくご紹介します。Pythonの環境設定が問題ない方はスキップしていただいて構いません。

Anacondaのインストール

まず。以下のリンクにアクセスします。

Download Anaconda Distribution | Anaconda

Anacondaのページ

Anacondaのページ

メールアドレスの入力欄がありますが、単純にAnaconda環境を構築したい場合には、「Skip registration」をクリックすることで、メールアドレスを入力せずにダウンロード画面に移動できます。

ダウンロード画面

ダウンロード画面

Windowsのインストーラーをダウンロードします。この画面における最新のバージョンは、Python 3.12です。

Anacondaのセットアップ

以下、セットアップ画面を順番に紹介します。基本的に、この画面と同じように選択や入力を行えば最低限の環境を整えることができます。

Anacondaのセットアップ1

Anacondaのセットアップ2

Anacondaのセットアップ3

※ここの[ユーザー名]は、ご自身の環境のものに置き換えてください。

Anacondaのセットアップ4

Anacondaのセットアップ5

Anacondaのセットアップ6

Anacondaのセットアップ7

Anacondaのセットアップ8

Anacondaのセットアップ9

以上で、Anacondaのインストールが完了です。

pymcのインストール

Anacondaのインストールが完了すると、スタート画面からAnaconda promptが起動できるはずです。
Anaconda promptにて、以下をコードをコピペして実行します。

conda install -c conda-forge pymc

仮想メモリを増加

もし、pymcをインストールできずにメモリ不足のような表示が出た場合は、以下の方法で解決できる可能性があります。

Windowsの仮想メモリ設定を変更

• 以下の方法で仮想メモリ（ページファイル）を増加させます。

  1. 「システムのプロパティ」を開く（Windowsキー + R → sysdm.cpl）。

  2. 「詳細設定」タブ → 「パフォーマンス」 → 「設定」。

  3. 「詳細設定」タブ → 「仮想メモリ」 → 「変更」。

  4. 「すべてのドライブのページング ファイル サイズを自動的に管理する」のチェックを外す。

  5. システムドライブを選択し、「カスタムサイズ」を設定（最小2048MB、最大8192MB）。

以上、pymcのインストールが無事完了すれば、MCMC-EAを動かすことが可能になるはずです。

MCMC-EAの作成方法まとめ

さて、最後に改めてMCMC-EAの作成方法をまとめます。

1. MLD-EAを稼働するために必要な以下の3ファイルを用意する。

   • MLD-EA_note.mq5

   • get_target_prices.bat

   • get_target_prices.py

2. get_target_prices.pyに「import pymc as pm」というコードを追加した上で、ターゲット価格計算方法をMCMC用のコードに置き換える。

3. pymcをインストールする。

MLD-EAを稼働することができている状態であれば、以上の3つを対応するだけでMCMC-EAへの拡張は完了するはずです。

なお、以下のページにてVPSの設定からEAの稼働までの詳細なガイドを用意しています。
ここで紹介しているEAとは異なるものを例にしていますが、MCMC-EAやMLD-EAを稼働させる上でも参考になると思います。あわせてご覧ください。

機械学習とFX自動売買：VPSの設定からML-EAの稼働までの完全ガイド » ナンピンマーチンEAの研究機械学習とFX自動売買：VPSの設定からML-EAの稼働までの完全ガイド