
クラスタリングの最適化(エルボー法)
ChatGPTに教えてもらいながらクラスタリングを整理。
クラスタリングは教師なし学習の一手法で、ラベルなしのデータを似た特性を持つグループに自動分類します。例えば、顧客データを異なるセグメントに分けることができます。アルゴリズムにはKMeans、DBSCANなどがあり、分類されたクラスタはデータ解析や推薦システムに利用されます。
ダミーデータの生成
クラスタが分散するようにクラスタ数=10で、100件のダミーデータをつくる。
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# クラスタ数が10のダミーデータを生成
X, y = make_blobs(n_samples=100, centers=10, random_state=42, cluster_std=1.0)
# データをプロット
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
plt.title("Original Data with 10 Clusters")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show() Feature 1 Feature 2
0 -7.985962 -8.076316
1 -10.650614 9.871789
2 4.963963 1.588087
3 7.170794 -5.456233
4 -8.741250 8.292168
・・・・
最適なクラスタ数(エルボー法)
クラスタ数を変えながらクラスタ内の距離の総和(SSE: Sum of Squared Errors)を計算する手法。
エルボー(肘)のように曲線が折れ曲がる点が適切なクラスタ数。
クラスタ数10で生成したダミーデータだが、エルボー法では3〜4が最適なクラスタ数となる。
# エルボー法によるクラスタ数の選定
sse = []
k_values = range(1, 11)
for k in k_values:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
sse.append(kmeans.inertia_)
# SSEをプロット
plt.figure(figsize=(10, 6))
plt.plot(k_values, sse, marker='o')
plt.xlabel('Number of Clusters')
plt.ylabel('SSE')
plt.title('Elbow Method For Optimal Number of Clusters')
plt.show()
KMeansクラスタリング
クラスタ数=3でクラスタリング。3つのグループに分類された。
from sklearn.cluster import KMeans
# KMeans クラスタリング(クラスタ数3)
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
labels = kmeans.labels_
# クラスタリング結果をプロット
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='rainbow')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], marker='x', s=300, c='black')
plt.title("Data after KMeans Clustering into 3 Clusters")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
高次元データのクラスタリングと可視化
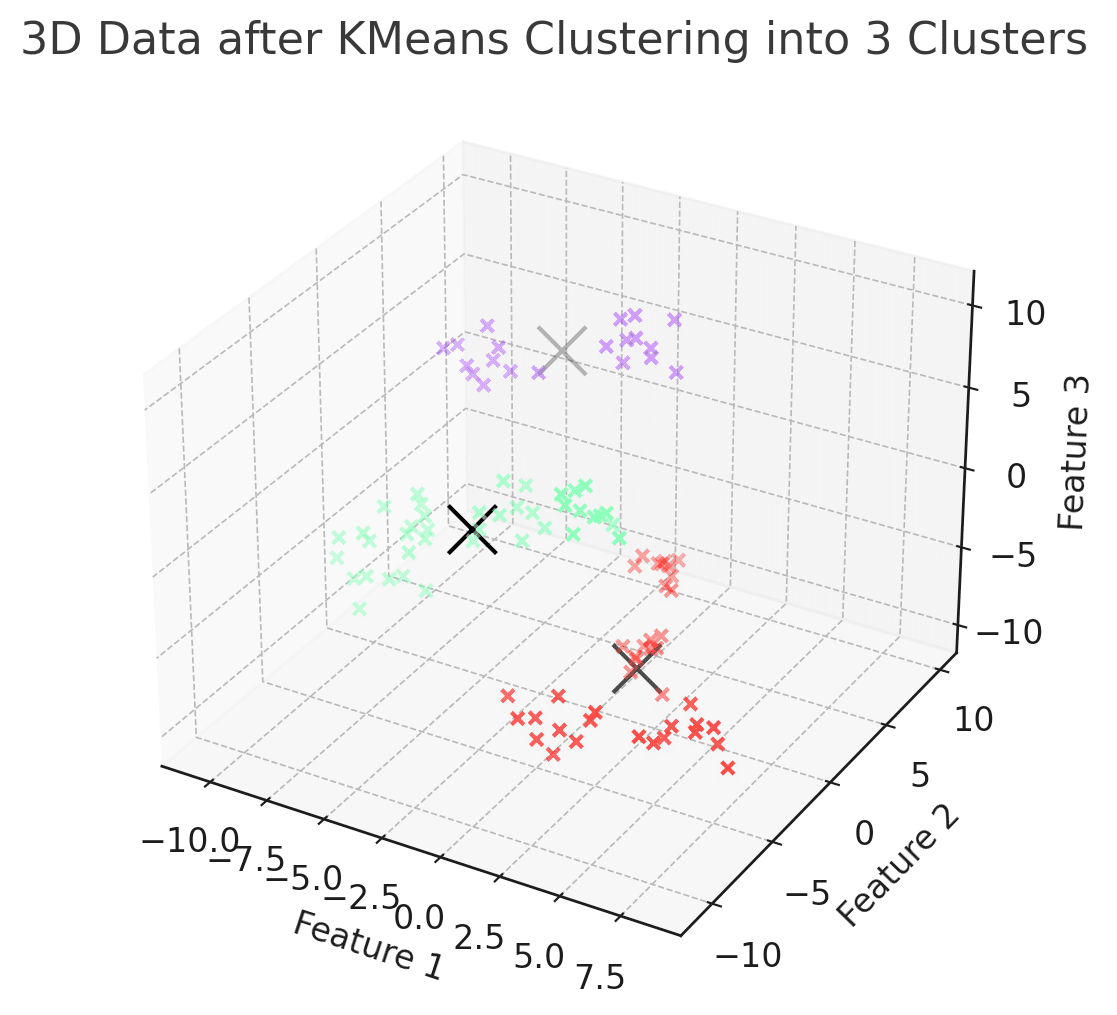
特徴量が3つでクラスタリング。2次元のときと考え方は同じ。
from sklearn.datasets import make_blobs
# クラスタ数が10の3次元ダミーデータを再生成
X_3d, y_3d = make_blobs(n_samples=100, centers=10, n_features=3, random_state=42, cluster_std=1.0)
# KMeans クラスタリング(クラスタ数3、3次元データ)
kmeans_3d = KMeans(n_clusters=3, random_state=42)
kmeans_3d.fit(X_3d)
labels_3d = kmeans_3d.labels_
# 3次元クラスタリング結果をプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_3d[:, 0], X_3d[:, 1], X_3d[:, 2], c=labels_3d, cmap='rainbow')
ax.scatter(kmeans_3d.cluster_centers_[:, 0], kmeans_3d.cluster_centers_[:, 1], kmeans_3d.cluster_centers_[:, 2], marker='x', s=300, c='black')
ax.set_title("3D Data after KMeans Clustering into 3 Clusters")
ax.set_xlabel("Feature 1")
ax.set_ylabel("Feature 2")
ax.set_zlabel("Feature 3")
plt.show() Feature 1 Feature 2 Feature 3
0 -0.290283 5.984511 -6.629224
1 6.351907 -10.578846 8.831899
2 -2.091466 -3.958959 2.282630
3 -0.846064 -3.661631 2.752106
4 -6.705136 -3.291352 -3.873060
・・・
4次元以上の場合も、次元削減を行うことで可視化できる。
4次元ダミーデータをクラスタ数=3でKMeansクラスタリングした後、PCA(主成分分析)を用いて次元削減し、2次元データにする。
from sklearn.decomposition import PCA
# クラスタ数が10の4次元ダミーデータを生成
X_4d, y_4d = make_blobs(n_samples=100, centers=10, n_features=4, random_state=42, cluster_std=1.0)
# KMeans クラスタリング(クラスタ数3、4次元データ)
kmeans_4d = KMeans(n_clusters=3, random_state=42)
kmeans_4d.fit(X_4d)
labels_4d = kmeans_4d.labels_
# PCAで2次元に次元削減
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_4d)
# 2次元プロットで可視化
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=labels_4d, cmap='rainbow')
plt.title("4D Data after KMeans and PCA")
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.show() Feature 1 Feature 2 Feature 3 Feature 4
0 -3.400107 4.347860 -0.790209 -3.039852
1 6.661855 -4.299684 -6.628157 -3.611741
2 -7.748544 8.400807 8.414226 6.659866
3 -0.331503 5.501327 -6.224206 1.383466
4 1.254433 3.751431 -6.158309 0.873006
・・・
