【線分図の魅力】平面図形の展開図
前回は、平面図形の周りの長さを、線分図を用いて求めてみました。(記事)
今回はこちら。
【問題 正四面体を切る】
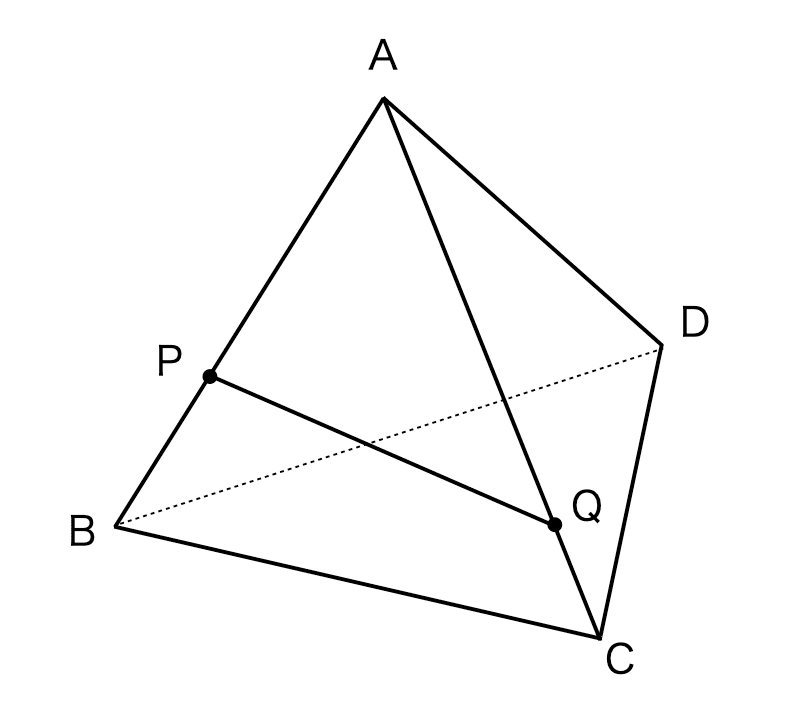
4つの面がどれも、1辺の長さが3cmの正三角形である三角すいA-BCDがあります。図のように、三角すいの辺AB上にはAP:PB=2:1となるように点Pを、辺AC上には三角形APQと四角形PBCQの周りの長さが等しくなるように点Qをとります。AQの長さは何cmですか。
【解説 平面図形を開いてみる】
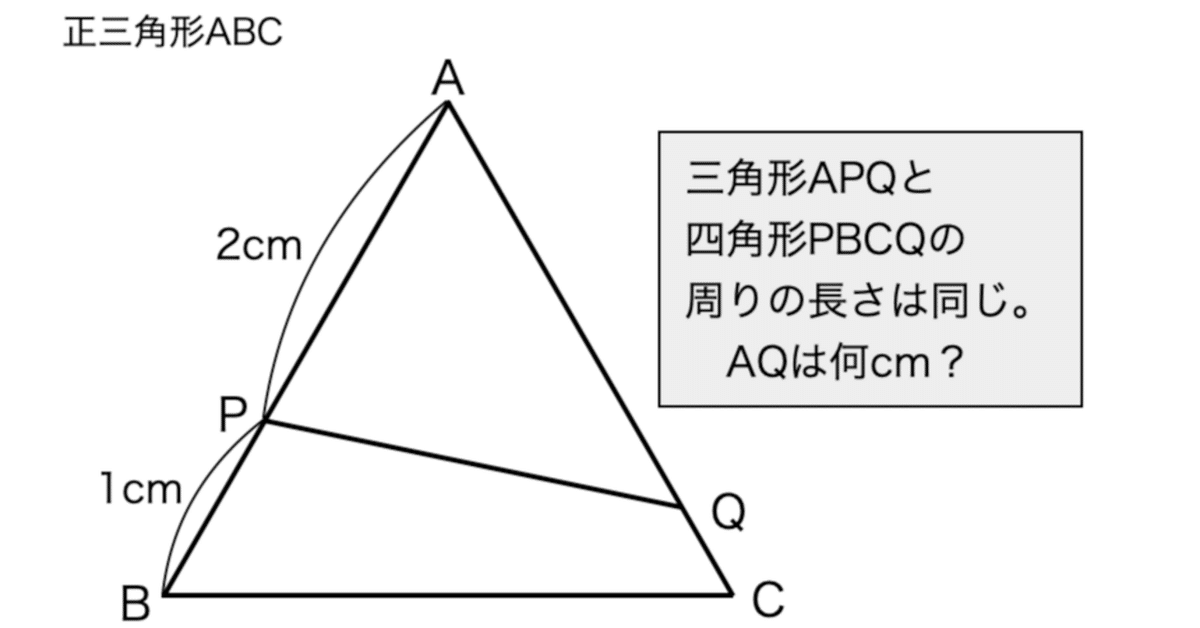
三角形ABCの平面以外の情報は今は要りません。AP:PB=2:1より、もちろん2cmと1cmです。

上の三角形と、下の四角形の周りの長さが等しいと言っていますので、図形を切り開いて線分図のようにすると、左右の端がそろいます。平面図形にも展開図があるんですね。

QAの長さとQCの長さの差は、4−2=2cmと分かります(赤い部分)。QAとQCは三角形の1辺だから合わせて3cmなので、和と差が分かりました。

AQ=(3+2)÷2=2.5cm
(上図で、CA=2cmに見えますが、向きをそろえて線を並べているため、長さは違います。)
【補足 線分図は「必要」?】
どんどん情報が小さくなるのが気持ち良いですね。この問題で線分図を使うメリットは、「周りの長さが同じ」ことが可視化されることです。もちろん、できる人は式だけで解く方が早いでしょう。和差算を学びたての人には楽しいチャレンジかも知れません。
ちなみにこの問題には(2)と(3)もあります。これは本当に立体。
2023年9月2日
いいなと思ったら応援しよう!

