
【算数】3つの集合の3つの問題
さほど頻出ではない集合分野の問題を頻繁に取り上げていることに自分で驚いています。むしろ少ないから個性を感じるのでしょう。ではどうぞ。
【問題】夏休みは山?海?それとも…
46人のクラスで夏休みに出かけた場所のアンケートをとったところ、山に行った生徒が12人、海に行った生徒が15人、遊園地に行った生徒が13人いました。
2か所だけに行った生徒が15人であるとき、次の問いに答えなさい。
(1) 山、海、遊園地の3か所に行った生徒はもっとも多くて何人ですか。
(2) 山、海、遊園地のうち、1か所以上に行った生徒はもっとも多くて何人ですか。
【回答】どこにも行きませんでした。
12+15+13=40か所…全員が行った場所の合計。
2か所×15人=30か所…「2か所に行った人」が行った場所の合計。
40−30=10か所…「1か所の人」と「3か所の人」が行った場所の合計。
(1)残り10か所を、できるだけ「3か所に行った人」で埋めたい。
10か所÷3か所/人=3人(あまり1か所)
(2)同様に、10か所÷1か所/人=10人…「1か所に行った人」の最大値。
15人+10人=25人
【分析】この問題のコアは何?
結局今何をしたのでしょう?ということで、問題を単純化してお見せします。
「りんごが12個と15個と13個あります。15人が2個ずつ食べました。残りを一人に3個ずつ分けるとしたら、何人に分けられますか?」
どうですか。小学2年生でもできますね。我々がいかに基本の知識を活用せず、物事を難しく考えているか、よく認識するべきだと思います。単純化のポイントは
①「山・海・遊園地」の区別は不要
②合計人数の「46人」は不要
ということです。せっかく「○か所」と書いてあるので、「○か所×人数=のべか所」と積の形で「のべか所」ベースでイメージするのが解決に近いです。いきなり46人‐15人=31人と人数ベースで考え始めると厳しいでしょう。
ところで、式だけで理解できれば良いのですが、何となく「本当かな?」と心配にもなりますので、視覚化を試みます。ここから本題。
【視覚化案①】万能と思われた「表」だが…

以前、桜蔭中の問題を題材に、この「3種の表」が強いと書いたのですが、この問題とは相性が悪すぎます。表は、「海と山に行った人の合計(ア)」などの具体的な情報は見やすく分けられるのですが、「どれか2か所に行った人(オカキ)」などという抽象的な部分を表すのはたいへん苦手なようです。というか、こんな小さい問題に使うものではない。
【視覚化案②】とりあえず「ベン図」で!

表よりは格段に分かりやすいです。問題に書いてある情報が比較的分かりやすい位置にあります。でも、この図を「使って」解くとしたら「エが最大ということはオカキが0になればよい」という理解を引っ張り出すことになるでしょうが、それが難儀です。それなら最初から式で解けると思います。結局ベン図も難しい。
【視覚化案③】次元を下げて「全部書く図」が最強
下のような図を捻り出しました。今回はこれで理解することををお勧めします。
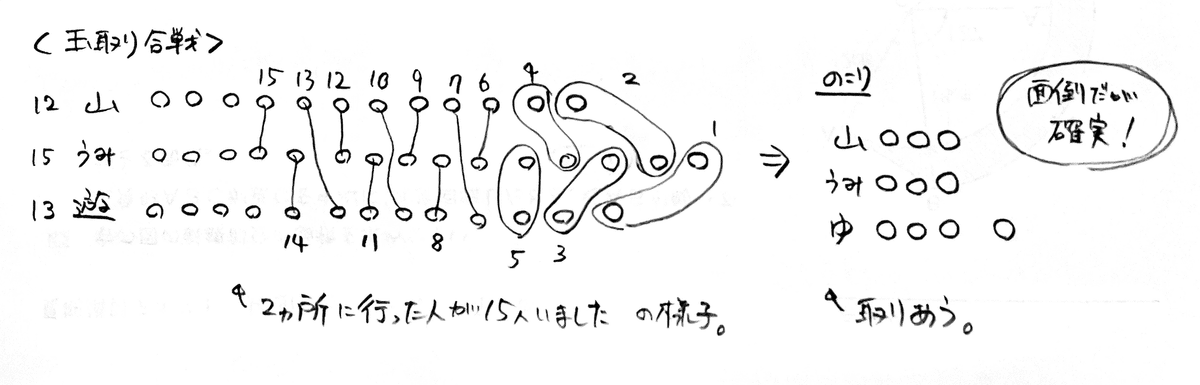
「山ボール」「海ボール」「遊園地ボール」を何種類持っているかで競い合う人たちの絵です。最初に解説した「12+15+13−2×15=10」が完璧に表現できています。これなら他の図表と違って「理解しなくても勝手に式と同じことができる」道具になっています。あくまで「上の解説の式を理解する」がゴールなので、大きい数だったらとかは知りません。
【補足】個々の残りの数は心配無用
上図のように、3種類のボールは途中から数が揃い、最後のわり算も数が変わってもキレイにできるので、残り数をあれこれ心配することはありません。※数がまだ揃っていない序盤は調べる必要あり。
また、視覚化案④として「面積図」があり、今回の状況をたいへんよく表現できますが、この図を書こうと思えるなら式を書くべきですので、載せません。あくまで「書いたから解ける」という、思考のはしごを目指します。
【おまけ問題】落ち溢れの炙り出し
なかなかユニークな問題でしたが、最近似た問題を見つけました。
40人の生徒がA,B,Cの3種類のテストを受けました。A,B,Cそれぞれの合格者は15人、18人、20人で、すべてのテストに合格したのは5人でした。このとき、どのテストにも合格していない人は最も多くて⬜︎人です。
縁起の悪い入試問題ですね…。。。
2023年10月29日
いいなと思ったら応援しよう!

