【算数】「⑩−３＝７−②」みたいのを全パターン調べて計算した結果。

いわゆる一次方程式と、中学入試との関わりについて。
中学受験では、一次方程式を扱う問題は基本問題としてごく多数出題されます。むしろ、ほとんどがこれに該当する問題と言ってもいいのかも知れません。算数では「つるかめ算」「いもづる算」など、様々な技術で不明な数を確定していきます。その中で、特に「消去算」「倍数変化算」で処理するような数の関係について検討します。これは、算数の講師でも教え方が大きく異なります。

テーマ：2種類の数の比を求める計算

この記事では「2種類の数」の関係を求める方法について書きます。例えば「①+500円と②−1000円が同じ」という条件から「①＝1500円」を求めたり、「□×3＝○×2」という比の関係を求めたりすることです。数学の表記だと「ax+by=0」となるような式です。
変数が3つ以上の場合は、事前に2つに減らす作業が入ります。

★これが全パターン。たぶん

まず課題を洗い出しました。
「⑩+3＝②+7」という大小関係の式をベースにいろいろ入れ替えて64通り試したところ、結局のところ種類・大小・符号の関係は以下の6パターンに絞られることが分かりました。
A　【⑩+3＝②+7】
B　【⑩−3＝②+7】
C　【⑩−3＝7−②】
D　【⑩−7＝②−3】
E　【⑩−7＝②+3】
F　【⑩−7＝3−②】
また、この中で、AとD、BとE、CとFの組はそれぞれ解が等しくなります。

■検討

これを中学受験生が一体どのように解くのが良いのかというのが問題です。特に、見るからに難解なC・Fパターンを問題なく処理できることが重要。
○課題１：どのパターンも同じ方法で解く。
○課題２：負の数を用いない。例えば、⑩−(②−3)＝⑩−②+3を避ける。
○課題３：なるべく減法の結合を用いない。例えば、⑩−3−7＝⑩−(3+7)を避ける。

---

検証①：線分図で整理する

よく、過去問の解説などでは線分図で説明されています。頑張って全パターン書いてみました。同じ答えになる組でも、図が異なる場合があります。

○12が打てないから、逆にすればよかった…

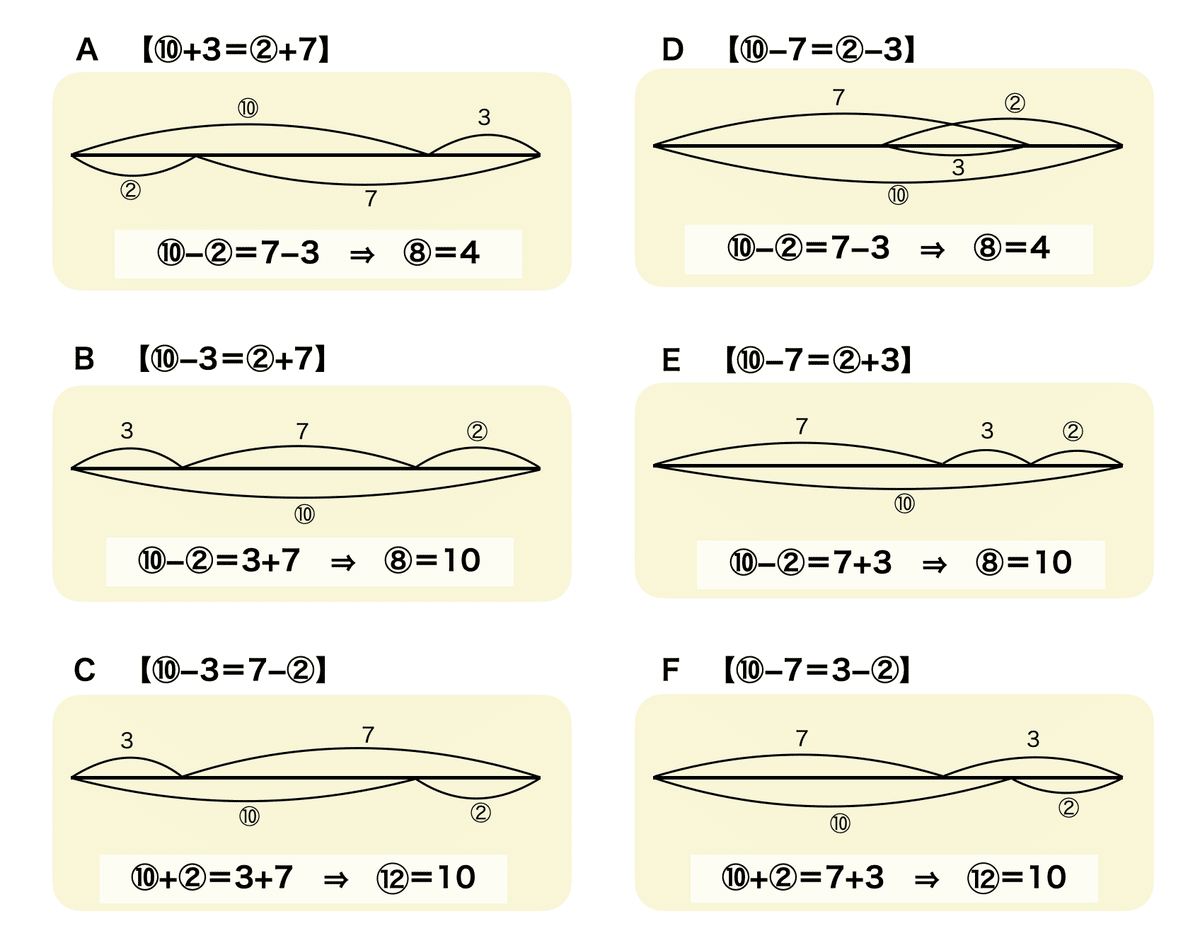
きれいに整理できていて計算が少ないですが、これを書くのはかなり難しいです。特に、C・Fについては、先に書いた線を延長する必要があります。また、Dのように重なる発想も出にくいです。効果的なルールとしては「同じ種類の数は必ず端点をそろえる」ということでしょうが、左右どちらに向かって書くかも難しいため、数に対する理解がかなりある人向けです。

---

検証②：困ったときの消去算

一次方程式は消去算と呼ばれる方法で大体処理できます。というのも、消去算はいわゆる連立方程式の解き方そのものに近いです。力技になったり混迷することがあるので場面を選びます。例えば…

⑩が②の倍数なので、これでも一行節約している

自ら未知の文字を一つ増やすことになります。また、式全体を何倍かした後、また割るところがとんでもなく面倒です。さらに、別パターンでそろえる数によっては負の数が出ます。そんなことができるくらいなら、別の方法を学ぶべきです。

---

次に、現状最も理解が良いという感触を持っている方法を示します。
よろしければ記事のシェアをお願いいたします。