2024 開成中 算数
初めての方はご一読ください。
受験者平均点 48.6点/85点
合格者平均点 58.3点/85点
2024年の開成中の算数です。昨年度と比べたら難化なのは間違いありませんが、開成の入試としては標準的といえそうです。それぞれの問題の最初のハードルが高いですが、乗り越えるべきポイントを確認しながら解いてみるとよく理解できるでしょう。
大問1(1)B (2)(ア)A (イ)C

(1)初っ端から作業と思考力の絶妙なバランスの問題。どの数字を使うかよりも、個数の推測から入れるとゴールに近づけたでしょう。
(2)アはやさしめ。イはどこで重さが等しくなるかを検討しなければなりません。この問題はグラフで考えると理解がしやすいです。ただ気づきにくいのも事実ですので、本番では検討するか感覚で攻めるか諦めて飛ばすかといった判断をすべき問題です。
(3)(ア)A (イ)A (ウ)A

ここは短時間で完答しない相当苦しくなってしまいます。
大問2(1) A (2)(ア)A (イ)A (ウ)①A ②A (エ)B (オ)C

場合の数ですが、調べ方がやさしい上に、分岐もさほど多くありません。
さらに、気づけば計算ですべて解けてしまいます。この大問で完答できると合格にぐっと近づけることでしょう。
大問3(1)A (2)A (3)B (4)B (5)B
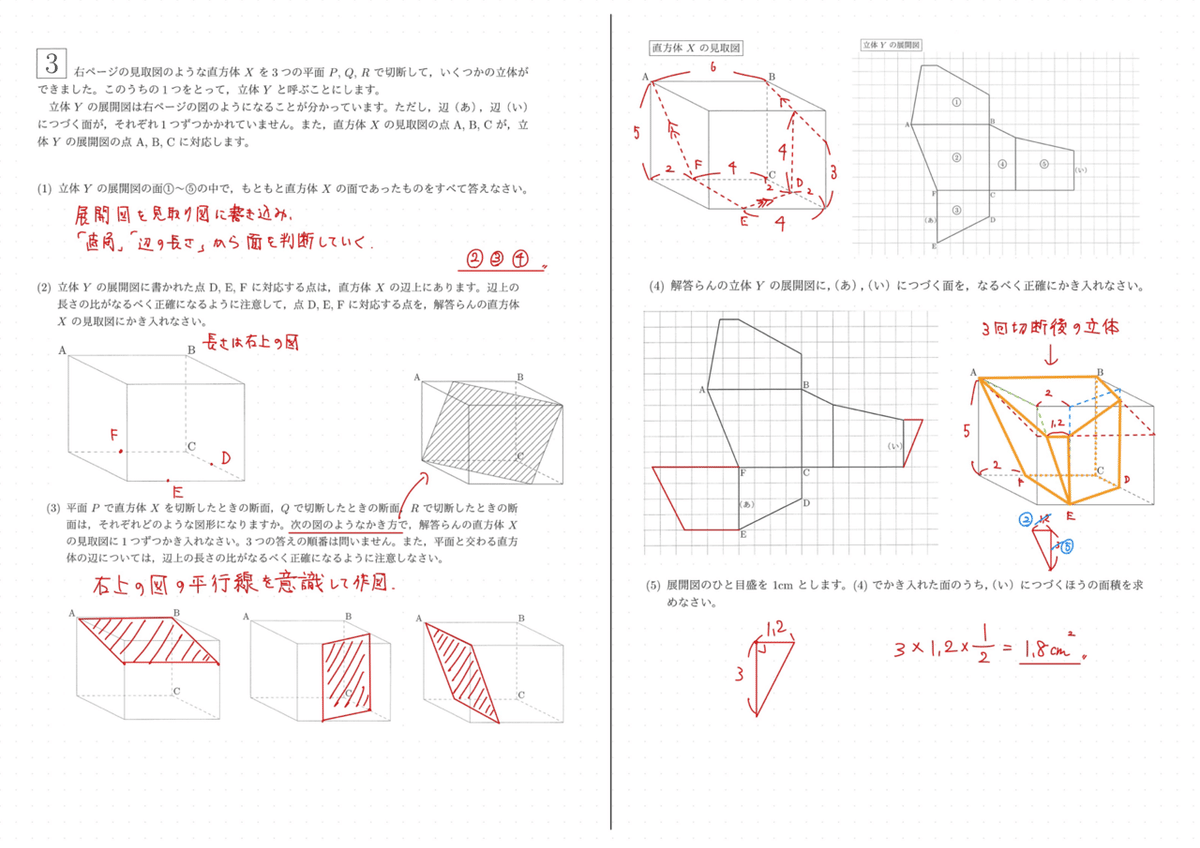
展開図と絡めた切断です。この出題は非常に開成らしいですね。過去にも開成中は立体図形の分析の仕方は多様な出題が多いです。ただ、既習の形、解き方に落とし込むことができ、技術系の問題としても解けるので、開成中に合格するふるいとなるにふさわしい問題でした。
全体的に答えやすい問題が多かった分、得点差がつきにくかったのでしょう。ただ、算数で他の受験生を引き離すことが十分できるセットであったといえます。私は授業では開成中の入試は何をしでかすか分からないと受験生によく言っています。どのような形でも対応できる基本の地力を鍛えていきたいですね。