
「二分探索木」(中級):OCaml演習 -46問目-
二分木についての練習問題と答案です。問題は、OCaml公式ページのものを使いました。答案の作成時間は、約5分でした。
問題46.
整数のリストから二分探索木を生成する関数constructを書け。
実行例
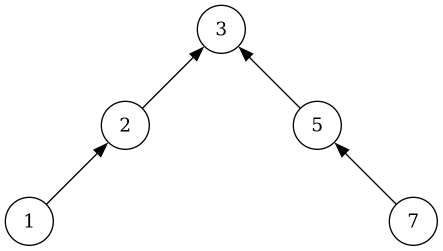
# construct [3; 2; 5; 7; 1];;
- : int binary_tree =
Node (3, Node (2, Node (1, Empty, Empty), Empty),
Node (5, Empty, Node (7, Empty, Empty)))
※ 前回と同様に二分木の型には以下の定義を用います。
type 'a binary_tree = Empty | Node of 'a * 'a binary_tree * 'a binary_tree
答案
本問の解き方
二分探索木とは、任意の節について、左部分木に含まれる全ての節の値が当該節の値よりも小さく、右部分木に含まれる全ての節の値が当該節の値よりも大きな二分木を言います。
この定義は再帰的になっています。
そこで、そのまま実装すれば答案となります。
コード
type 'a binary_tree = Empty | Node of 'a*'a binary_tree*'a binary_tree
let rec append x comp = function Empty -> Node (x, Empty, Empty)
| Node (label, left, right) ->
if comp x label = 0 then Node (label, left, right)
else if comp x label < 0 then Node (label, append x comp left, right)
else Node (label, left, append x comp right)
let construct lst =
let comp x y = x-y in
let rec loop tree = function [] -> tree
| head::tail -> loop (append head comp tree) tail in
loop Empty lst
関数appendは、二分探索木に所与の整数を値とする節を付け加えます。
感想
今回の問題は、前回と同様に簡単でした。
関数型プログラミングについての理解が深くなってきたので、「本問の解き方」の内容がどんどん浅くなっています。
決して、面倒くさくなったからではありません。
今回の記事では、再帰的定義から如何にして再帰的な構成方法を導くのかについて「そのまま実装」と書きました。
「そのまま実装」では分かり難かったかもしれません。
もう少し具体的に言うと、定義を繰り返し読んでいるとあれがボワァと浮かび上がってくるので、キュッキュッとして下さい。そうすると、バーンとなってコードができあがります。
浮かび上がったときに、グッとするとパラッとなるかもしれないので注意してください。
次回は、第47問です。今回はC言語のコードも作成するつもりだったのですが、リストと二分木の両方の定義を載せると長くなりすぎるので止めました。
いいなと思ったら応援しよう!

