
宇崎ちゃんコラボのSCM解析の弱点を突かれたので、何かしてみる。その3
パラレル仮定が成立してないけど、どうする?
その1でまとめましたように、パラレル仮定は成立していないっぽいです。パラレル仮定2については、その2でまとめたとおりです。
ここでは、パラレル仮定1について検討したいと思います。
パラレル仮定1を何とかならないか、考える。
では、次の問題点です。パラレル仮定1は下記の様に定義しました。
パラレル仮定1:関東と合成対照は、宇崎ちゃんコラボ前期間(~2019年9月)の献血者数の動きについて、パラレルな動きをしている。
※観察可能
下のグラフを見て頂ければわかりますように、これは成り立っていると言うには若干無理があります。もし、成り立っているのであれば、横一直線(に近い)グラフになっているはずですから。

どうしよう?
どうするかは、Haluco【JK1】様から頂いたツイートをヒントにしました。
ぱっと見で感じるのは差分は3ヶ月毎のリピーターの存在では?(400ml献血は3ヶ月空けないと出来ない、因みに女性は4ヵ月空けないと出来ない)
— Haluco【JK1】 (@HalucoJK1) July 17, 2020
2、5、8月は一致しているのに10月はイレギュラー。
ランダムウォークと言うには綺麗だなと。
つまり、このグラフには3ヶ月周期があるのではないか?というご指摘です。

前提として、「このグラフはランダムウォークではない(その1参照)」ことがあります。これは逆に言うと、「ある法則に則った動きがある」ということです。
見てみると、2019年11月から2019年9月まで確かに「多い、減る、一寸増える」というサイクルが繰り返されていることに気づきます(今更気づくわけです)。
ここでは、2018年11月~2019年9月の11ヶ月分のデータを用いて、「ある法則(式)」を推定します。
そして、「ある法則(式)」が2019年10月にも働いていたら、このグラフはどうなっていたか?を計算することができます。
その計算値が実測値が大きく異なっていたら、その法則からズレるような何かが2019年10月にはあったと考えられます。
こういった方法で、パラレル仮定1が崩れているにもかかわらず、2019年10月には、偶然誤差を超えた変化が観察されたのではないか?を検証してみたいと思います。
ARMAモデルで時系列解析
まず、この時系列データには単位根がないことは確認済みです(伏線回収)。
先にデータセット(という程でもありませんが)とStata doファイルを公開しておきます。
この時系列データをARMAモデルで2018年~2019年9月を解析してみようと思います。ボロが出る前に白状しておくと、ARMAモデルで解析したのは2016年1月以来です。まぁ、完全に忘れてるわ! なお、その時は、ARIMAモデルとかARCHモデルもやってたらしい(健忘症発症中)。ARIMAといっても神戸の温泉地ではありません。
ARMAモデルは、日本語で言うと自己回帰移動平均モデルです(情報量が増えてません)。次のような式で、過去のデータY(今回で言うと、関東と合成関東の献血者数の差)が現在のデータYにどのように影響を与えているかを推定します。突然出てきたεは時間によって発生するランダムな数(ホワイトノイズ)とでも考えて下さい。投げやりになった。

ARMAモデルを構築する上で問題になるのは、式中のpとqをどのように決定するかです。つまり、どのくらい過去を考慮するのかを決めないといけません。
AR(p)とMA(q)を決定するための4つのステップ
最初に白状しておくと、下記は自分が2016年頃に書いた論文をDeepLで翻訳して、少し弄っただけです。詳細は成書(例えば、下記)を読んだ方が良いと思います。
ステップ1:自己相関関数(ACF)と部分自己相関関数(PACF)を用いて時系列データの定常性を確認します(いきなり分からんwww)。ACFとPACFは、自己相関と部分自己相関の情報を可視化します。
グラフの横軸はLagです。1ヶ月前からxヶ月前までの自己相関(あるいは部分自己相関)が計算されています。今回は、Lag=1から3までの自己相関と部分自己相関を計算しました(とういか、データ数が足りないので、Lag=4以上の算出はできません)。
ステップ2:ACFとPACFを見て、AR(p)とMA(q)のpとqの値の候補を決定した。グラフの灰色の影を越えているところが候補です。
ACFはMA(q)の候補を選択し、PACFでAR(p)の候補を選択します。
ステップ3:候補となったpとqに基づいて残差チェックを行います。モデルが適切であれば、残差はホワイトノイズになるはずです。これを確認するために、Box-Jenkins Q 検定(Box & Pierce, 1970)を用いました。
Q 統計量のp値が0.9より小さい場合、候補モデルは不適格とします。ただ、今回のデータでは、全てのモデルで0.9より小さかったです。これはデータ数が少ないためと思われます。今回はこの検定による除去は行えませんでした。
ステップ4:残った候補モデルについて赤池情報基準(AIC)を計算し、AICが最も小さいモデルを選択します。
簡単ですね!(白目)
結局選んだARMAモデルは、どんなモデルか?
ステップ1の結果:ACFとPACFのグラフ(コレログラム)を表記します。
上がACFで、下がPACFです。いずれも灰色の影を越えているのは、Lag=3のところです。PACFは確かに越えていますが、ACFは微妙です。取りあえず、3ヶ月前に注目するのが良さそうです。なお、使ったデータは11ヶ月分だけで短いので、Lagをこれ以上増やせない仕様でした。

ステップ2の結果:ここから判断すると、p=3/q=3またはp=3/q=なし、が候補になりそうです。これをAR(3), MA(3)とAR(3)と記載します。このどちらのモデルが良いか、ガチンコで真剣勝負します(フラグ)!
ステップ3の結果:Box-Jenkins Q 検定の結果を示します。AR(3), MA(3)ではp=0.563で、AR(3)ではp=0.727でした。両方とも0.9を下回っています。ここで両方とも却下すると、ここで終わってしまいます。見なかった事にしましょう! 真剣勝負とは?(フラグ回収)
ステップ4の結果:ガチンコの真剣勝負を生き残った2つのモデルを選択するために赤池情報基準(AIC)を算出します。これは小さければ小さいほど、予測能力が高いモデルと判断されます。
AR(3), MA(3)ではAIC=133.75で、AR(3)ではAIC=135.05でした。僅差ですが、AR(3), MA(3)が優れています。
モデル選択勝負の結果をまとめたのが、下記です。

どっちもどっちやな。
式にキチンと書くと下記の様な感じです。

どっちもどっちの性能のようなので、両方でやってみようと思います。
ARMAモデルによる将来予測
モデルが正しく、この傾向が2019年10月も続いていたとしたら、2019年10月の差(関東と合成関東の差)はどのようだったかを計算することができます。
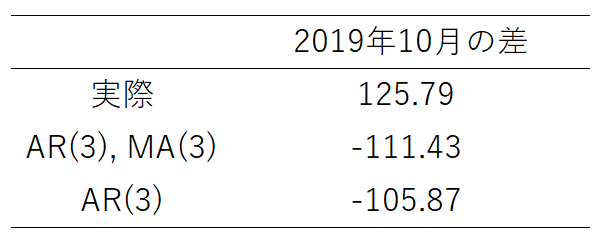
もし、2019年10月に何もなく推移していたら、合成関東に比べて、関東が100以上少なかったようです。
しかし、実際は、約+126であることから、やはり2019年10月には何かあったと考えて良さそうです。
ここで、注意して頂きたいのは、「モデルが正しく、この傾向が2019年10月も続いていたとしたら」という条件が、ついていることです。パラレル仮定1が成り立たないから、いろいろ考え出したのに、違う条件が必要になっています。
まとめ
ARMAモデルが正しい(少なくとも、ある程度は現実を反映している)としたら、2019年10月は関東とう合成関東の差マイナス100位になるはず。しかし、実際は約プラス126なので、2019年10月には何かあったと考えてよさそう。
利益相反(COI)について
宇崎ちゃん献血コラボ関係の利益相反は、2019年11月17日の記事中の通りです。
また、コメントを頂いた方々やTweet等を引用させて頂いた方との利益関係はありません。様々なご意見・ご指摘を頂きありがとうございました。
金銭・経済的なCOIはありません。ただし、金銭を頂くことを拒否している訳ではありません。何か贈りたい方は是非お願いします(ダイマ)。
