Matplotlibでグラフ（散布図、検量線まで引いてみる）

ここでは散布図を描いてみます。

散布図の基礎

散布図は以下の描き方があります。

・pltを使う(%matplotlib inline) 場合： plt.scatter()

・オブジェクト指向（コードで解決する）場合 : ax.scatter()

2種類で描くことができます。

筆者は前者で進めますが、念のため後者も記述します。

散布図を作成

散布図を作成するには、

plt.scatter(x,y) #散布図を描く

plt.show() #図を公開

を使用します。

では、乱数を使って散布図を描いてみましょう。

x = np.linspace(0,1,50)# 0~1の区間を50等分
y = np.random.rand(50)# ランダムに50作成
plt.scatter(x,y)
plt.show()

実行結果：

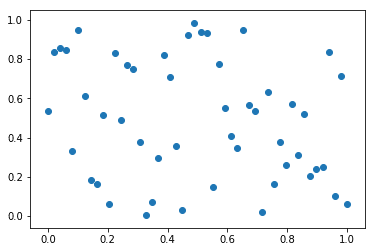
となります。

ちなみに、オブジェクト指向だと以下。

fig,ax= plt.subplots()　#土台とaxを同時に任命
ax.scatter(x, y)
plt.show()

同じグラフになります。

複数系列の散布図

複数の系列の散布図を描きたい場合、単純に、plt.scatter()を足せば問題なし。同じ要領で、3個目、4個目も可能。

x = np.linspace(0,1,50)
y = np.random.rand(50)
x2 = np.linspace(0,1,50)
y2 = np.random.randn(50)

plt.scatter(x,y)
plt.scatter(x2,y2)
plt.show()

実行結果：

デフォルトで色を変えてくれます。便利です。

プロットのサイズを変える

散布図のブロットのサイズを一括変換する場合は、plt.scatter()の引数にs= ○○を足せばよい。

x = np.linspace(0,1,50)
y = np.random.rand(50)
x2 = np.linspace(0,1,50)
y2 = np.random.randn(50)

plt.scatter(x,y,s=100)
plt.scatter(x2,y2)
plt.show()

事項結果：

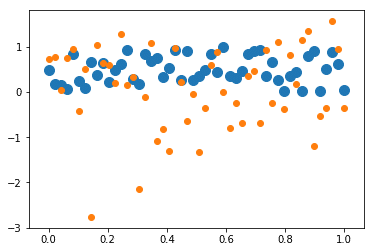
青のプロットが大きくなったのが分かるでしょうか。

バブルチャート

散布図でも、各プロットの特徴量に応じてプロットサイズを変更することができます。2次元のデータに大きさを加えることができるので、バブルチャートは便利です。

size = 300*np.random.rand(25)
print(size)

実行結果：

[ 72.41445402 137.1341471  111.4330074 ・・省略・・ 20.06825615]

こちらのsizeを使ってバブルチャートを作成します。

plt.scatter(x, y, s=size)
plt.show()

実行結果：

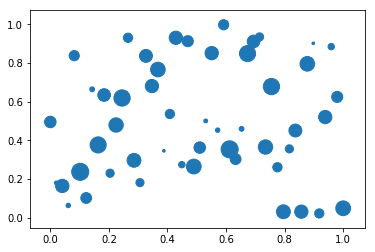
散布図に、データの大きさまで加えられ、分かり易いと個人的には思っています。

散布図に検量線を引いてみる（一次元)

検量線とは、簡単に言うとデータを1本の直線に集約すること。散布図で分布している要素を一次式 ax+b で近似してみます。

nampy で試す場合、np.polyfit()関数を使います。

np.polyfit(x, y, 1)#最後の1は一次式の1です

実行結果：

array([0.09060175, 0.4546613 ])

戻り値がそのまま係数、a、b に相当するため、

y=0.09060175x + 0.4546613
が近似式になります。

この式で 自力で y を計算してもいいのですが poly1d という便利な関数を使います。この関数にxを渡せば、計算までこなしてくれます。

func = np.poly1d(np.polyfit(x, y, 1))
func(x)

実行結果：

array([0.4546613 , 0.45651031, 0.45835933, 0.46020834, 0.46205736,・・・

では、散布図に検量線をプラスします。

plt.scatter(x , y)
plt.plot(x, np.poly1d(np.polyfit(x, y, 1))(x))

実行結果：

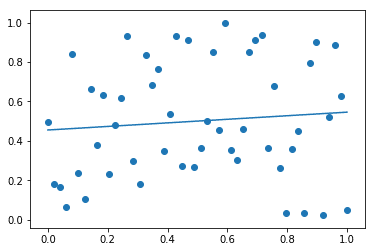
検量線が引けました。

散布図に検量線を引いてみる（二次元)

polyfit のパラメータを変えるだけで次数は簡単に変更できます。
2次式 ax2+bx+c で近似すると、

plt.scatter(x , y)
plt.plot(x, np.poly1d(np.polyfit(x, y, 2))(x))

実行結果：

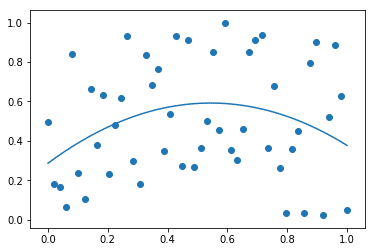
ということで、この次元を変えるとどんどん近似式は学習データに近づこうとします。しかし、次元を増やし過ぎると過学習になるため、注意が必要です。

scipy を使って検量線をかく

もっと単純に検量線を描きたい時は、scipyのインポートがお薦め。scipyは多変量解析などが得意です。

import scipy as sp
param = sp.polyfit(x,y,1)#ここで次元を教え込みます

param

実行結果：

array([0.09060175, 0.4546613 ])

はい、戻り値がそのまま係数、a、b に相当するため、

y=0.09060175x + 0.4546613
が近似式になります。

これをグラフに持ち込むと・・

param[0]は、0.09060175

param[1]は、0.4546613

plt.plot(x,param[0]*x + param[1])
plt.scatter(x,y)

実行結果：

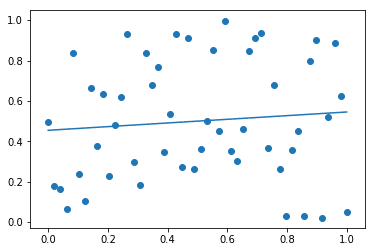
となります。