機械学習を用いたS&P500の価格変動予測と投資シミュレーション
1. はじめに
Python初学者の似非エンジニアさくらです。
元々インフラエンジニアを生業としていたので、ネットワークやサーバ、クラウド関連の知識はありますが、コードを書くことがあまりなく、1つくらいはきちんと書きたい!と思い、Pythonを学び始めました。
本記事は学習のアウトプットの一環として、投稿しています。初学者のため、思慮不足な点はあるかと思いますが、ご一読いただけると幸いです。
なお、本記事は
データ分析をどのようなフローでどうやって実施しているか知りたい!
ファイナンスに興味があり、実データを使ったデータ分析を実施したい!
という方に読んでいただければと思います。
読まれた方はぜひ一緒に学習していきましょう!
2. 目的と概要
2-1. 目的
過去の株価データを基に作成した予測モデルを用いて、S&P500の株価が上がるのか下がるのかを予測します。
2-2. 概要
本記事では、2019年1月~2020年12月のS&P500の株価データから予測モデルを作成し、2021年の株価予測をするものとします。
今回用いる機械学習の手法は、「線形回帰(重回帰分析)」を用います。
理由は、2つあります。
連続値をとる対象で最も伝統的で、基本となる線形回帰分析となり、テクニカル分析の1つとしても存在するため
株価の決定要素は様々であり、複数要素を用いて、評価を行いたいため
今回要素として用いる指標は、S&P500と関連性があると思われる以下の6つの指標とします。
①米国10年債券の価格
②ナスダック100指数の価格
③ダウ平均株価の価格
④ドルインデックスの価格
⑤米国原油の価格
⑥米国ゴールドの価格
上記を説明変数とし、S&P500の価格データを目的変数とします。
なお、今回の学習・評価では、価格は週次データを用います。
3. データの取得と整形
3-1. 目的変数(S&P500)のデータ取得
S&P500の価格データをyahooファイナンスからします。
はじめに、株価データの取得に必要となるライブラリとデータの整形に必要となるライブラリをインポートします。
なお、yahooファイナンスからのデータ取得はyfinanceというライブラリを用います。
## ライブラリーのインポート
import yfinance as yf
yf.pdr_override()
import datetime as dt
import numpy as np
import pandas as pd
import pandas_datareader.data as pdr
import matplotlib.pyplot as plt続いて、yahooファイナンスからS&P500の株価データを取得します。
## S&P500の株価データ取得
### 期間の指定
start = '2018-12-01'
end = '2021-12-31'
### DataFrameの作成とデータの取得
df_spx = pdr.get_data_yahoo('^GSPC',start,end)取得したデータを表示すると下記のようになります。
取得開始日を2018-12-01としているのは、週次差分のみでなく、月次差分も説明変数で利用するためです。

3-2. S&P500のデータ整形
取得したS&P500の日次データから週次データに変換を行います。
同時に、下記のデータ整形も行います。
不要な列の削除:
”Adj Close”、"Volume"の削除
週次差分の計算:
金曜の終値(”Close”)を用いて、当週 - 前週の結果を"Close_Diff"に挿入
月次差分の計算:
金曜の終値("Close")を用いて、当週 - 4週前の結果を"Close_Diff_M"に挿入
## データ整形処理
### 不要な列の削除
df_spx = df_spx.drop(['Adj Close','Volume'],axis=1)
### 日次→週次変換
agg_dict = {'Open': 'first',
'High': 'max',
'Low': 'min',
'Close': 'last'
}
df_spx_w = df_spx.resample('W-FRI').agg(agg_dict)
### 列追加と差分計算
df_spx_w['Close_Diff_W'] = df_spx_w['Close'].diff()
df_spx_w['Close_Diff_M'] = df_spx_w['Close'].diff(4)
整形後の出力結果は下記の通りです。

最後に、データ整形後の週次差分の推移を折れ線グラフで可視化し、確認したいと思います。
## 可視化
plt.figure(figsize=(30,10))
x = df_spx_w.index
y1 = df_spx_w['Close_Diff_W']
y2 = df_spx_w['Close_Diff_M']
plt.title('S&P500')
plt.grid(True)
plt.plot(x,y1,color='b',label='Weekly')
plt.plot(x,y2,color='r',label='Monthly')
plt.legend()
plt.show()
3-3. 説明変数のデータ取得
目的変数と同様の処理を説明変数となる6指数に対して行います。
### 米国10年債券
df_tnx = pdr.get_data_yahoo('^TNX', start, end)
df_tnx = df_tnx.drop(['Adj Close','Volume'],axis=1)
df_tnx_w = df_tnx.resample('W-FRI').agg(agg_dict)
df_tnx_w['Close_Diff_W'] = df_tnx_w['Close'].diff()
df_tnx_w['Close_Diff_M'] = df_tnx_w['Close'].diff(4)
### ナスダック100指数
df_ndx = pdr.get_data_yahoo('^NDX',start,end)
df_ndx = df_ndx.drop(['Adj Close','Volume'],axis=1)
df_ndx_w = df_ndx.resample('W-FRI').agg(agg_dict)
df_ndx_w['Close_Diff_W'] = df_ndx_w['Close'].diff()
df_ndx_w['Close_Diff_M'] = df_ndx_w['Close'].diff(4)
### ダウ平均
df_dji = pdr.get_data_yahoo('^DJI',start,end)
df_dji = df_dji.drop(['Adj Close','Volume'],axis=1)
df_dji_w = df_dji.resample('W-FRI').agg(agg_dict)
df_dji_w['Close_Diff_W'] = df_dji_w['Close'].diff()
df_dji_w['Close_Diff_M'] = df_dji_w['Close'].diff(4)
### ドルインデックス
df_dxy = pdr.get_data_yahoo("DX-Y.NYB",start,end)
df_dxy = df_dxy.drop(['Adj Close','Volume'],axis=1)
df_dxy_w = df_dxy.resample('W-FRI').agg(agg_dict)
df_dxy_w['Close_Diff_W'] = df_dxy_w['Close'].diff()
df_dxy_w['Close_Diff_M'] = df_dxy_w['Close'].diff(4)
### 米国原油
df_oil = pdr.get_data_yahoo("USO",start,end)
df_oil = df_oil.drop(['Adj Close','Volume'],axis=1)
df_oil_w = df_oil.resample('W-FRI').agg(agg_dict)
df_oil_w['Close_Diff_W'] = df_oil_w['Close'].diff()
df_oil_w['Close_Diff_M'] = df_oil_w['Close'].diff(4)
### 米国ゴールド
df_gold = pdr.get_data_yahoo("GC=F",start,end)
df_gold = df_gold.drop(['Adj Close','Volume'],axis=1)
df_gold_w = df_gold.resample('W-FRI').agg(agg_dict)
df_gold_w['Close_Diff_W'] = df_gold_w['Close'].diff()
df_gold_w['Close_Diff_M'] = df_gold_w['Close'].diff(4)データ整形後の出力結果一覧は下記の通りです。

3-4. データ統合
ここまでで、目的変数と説明変数すべてのデータ取得と整形が完了です。
ここからは、取得・整形したデータの統合と調整を行います。
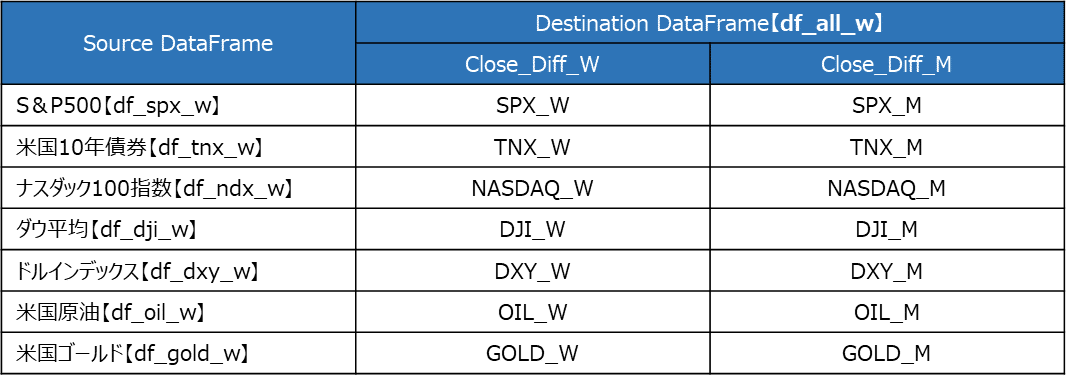
今回、学習・評価に必要となるデータは、目的変数と説明変数の「週次差分"Close_Diff_W"」と「月次差分"Close_Diff_M"」のみのため、各変数のそれ以外の列データを削除し、一つのDataFrameに統合します。
DataFrameの統合時に、列名が重複するため、統合時に各データの名前に合わせて、列名を変更後に、見やすいように列名の並び替えを実施します。
## dfの統合とリネーム
### SPX & TNX
df_all_w = pd.merge(df_spx_w,df_tnx_w,on='Date',suffixes=['_left','_right'])
df_all_w = df_all_w.drop(['Open_left','High_left','Low_left','Close_left','Open_right','High_right','Low_right','Close_right'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W_left' : 'SPX_W',
'Close_Diff_M_left' : 'SPX_M',
'Close_Diff_W_right' : 'TNX_W',
'Close_Diff_M_right' : 'TNX_M'
})
### df_all_w & NASDAQ
df_all_w = pd.merge(df_all_w,df_ixic_w,on='Date')
df_all_w = df_all_w.drop(['Open','High','Low','Close'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W' : 'NASDAQ_W',
'Close_Diff_M' : 'NASDAQ_M'})
### df_all_w & DJI
df_all_w = pd.merge(df_all_w,df_dji_w,on='Date')
df_all_w = df_all_w.drop(['Open','High','Low','Close'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W' : 'DJI_W',
'Close_Diff_M' : 'DJI_M'})
### df_all_w & DXY
df_all_w = pd.merge(df_all_w,df_dxy_w,on='Date')
df_all_w = df_all_w.drop(['Open','High','Low','Close'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W' : 'DXY_W',
'Close_Diff_M' : 'DXY_M'})
### df_all_w & US OIL
df_all_w = pd.merge(df_all_w,df_oil_w,on='Date')
df_all_w = df_all_w.drop(['Open','High','Low','Close'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W' : 'OIL_W',
'Close_Diff_M' : 'OIL_M'})
### df_all_w & US GOLD
df_all_w = pd.merge(df_all_w,df_gold_w,on='Date')
df_all_w = df_all_w.drop(['Open','High','Low','Close'],axis=1)
df_all_w = df_all_w.rename(columns = {'Close_Diff_W' : 'GOLD_W',
'Close_Diff_M' : 'GOLD_M'})
## 列の並び替えとNaN削除
df_all_w = df_all_w.reindex(columns=['SPX_W','TNX_W','NASDAQ_W','DJI_W','DXY_W','OIL_W','GOLD_W','SPX_M','TNX_M','NASDAQ_M','DJI_M','DXY_M','OIL_M','GOLD_M'])
df_all_w.drop(['2018-12-07','2018-12-14','2018-12-21','2018-12-28'],inplace=True)
データ統合と調整後を可視化してみます。
今回は各変数単体のグラフと1つのグラフにまとめたグラフを週次差分で表示します。


4. データの加工
図3. 1つにまとめた折れ線グラフを見てみると、株価の価格と変動幅が大きく異なることが分かります。
そのため標準化を行い、各指数の学習と評価の適正化を行います。
今回はsklearnに含まれるStandardScalerは使わずに、applyメソッドで、DataFrame内のすべての行に【(値 - 平均) / 標準偏差】のlambda関数を渡し、標準化を行います。
## 標準化
df_all_w_std = df_all_w.apply(lambda x:(x-x.mean())/x.std(),axis=0)標準化実施後の変数一覧を折れ線グラフは下記の通りとなります。


5. モデルの作成と学習
ここまでで、学習・予測を行うデータの整形と加工ができたため、線形回帰(重回帰分析)にてモデルの作成と学習を行います。
今回の学習・予測では、期間指定による学習データと予測データの分割を行う必要があるため、標準化後のDataFrameに対して、期間に応じた分割を行います。
なお、目的変数となるS&P500と説明変数となるナスダック100およびダウ平均は銘柄の包括度がかなり高い(ダウ平均銘柄はすべてS&P500に包括される)ため、一度説明変数から除外します。
また、目的変数が週次データを対象としているため、説明変数も週次データのみを対象とします。
## ライブラリのインポート
from sklearn.linear_model import LinearRegression
## 学習データと評価データの定義
### 学習データと評価データの分割
df_train = df_all_w_std['2019-01-01':'2020-12-31']
df_test = df_all_w_std['2021-01-01':]
### 学習データを説明変数と目的変数に分割
X_train = df_train[['TNX_W','DXY_W','OIL_W','GOLD_W']]
y_train = df_train[['SPX_W']]
### 評価データを説明変数と目的変数に分割
X_test = df_test[['TNX_W','DXY_W','OIL_W','GOLD_W']]
y_test = df_test[['SPX_W']]
## 可視化
fig = plt.figure(figsize = (30,10),facecolor="skyblue", tight_layout=True)
x1 = y_train.index
x2 = y_test.index
y1 = y_train
y2 = y_test
plt.grid(True)
plt.plot(x1,y1,color='k',label='Train Data')
plt.plot(x2,y2,color='r',label='Test Data')
plt.legend()
plt.show()
6. 予測と精度評価
図5. 学習データと評価データの分割で赤線となっている期間を予測します。
では、実際に予測と精度を評価しましょう。
## 予測実施
model = LinearRegression()
model.fit(X_train,y_train)
model.score(X_train,y_train)
pred = model.predict(X_test)
model.score(X_test,y_test)
## 結果の可視化
fig = plt.figure(figsize = (30,10),facecolor="skyblue", tight_layout=True)
x1 = y_train.index
x2 = y_test.index
y2 = y_test
y3 = pred
plt.grid(True)
plt.plot(x1,y1,color='k',label='Train Data')
plt.plot(x2,y2,color='r',label='Test Data')
plt.plot(x2,y3,color='b',label='Pred Data')
plt.legend()
plt.show()実行結果は下記となりました。


図6. 評価データと予測結果のグラフを見るとわかるように、一部分を除き、評価データに比べ、値動きが穏やかになっています。
これは表7. 決定係数の結果にも表れており、決定係数が0.135と低く、これは目的変数(S&P500の予測したい株価データ)に対して、説明変数(関連すると仮説を立てた米国10年債券、ドルインデックス、米国石油、米国ゴールド価格の値動き)が当てはまり度が低いことを指しています。
学習データでは、決定係数が0.462とどちらかというと悪い数値になっていることもわかります。
7. モデルのチューニング
6.予測と精度評価で想定以上に悪い結果となったため、モデルのチューニングを実施したいと思います。
今回実施するのは2パターンのチューニングを行います。
パターン①:
説明変数の種類は変えず、月次差分のデータを追加する
パターン②:
説明変数に除外していたナスダック100とダウ平均を追加する
それでは実施してみましょう。
7.1 パターン①
### 学習データを説明変数と目的変数に分割
X_trainA = df_train[['TNX_W','DXY_W','OIL_W','GOLD_W','DXY_M','OIL_M','GOLD_M']]
y_trainA = df_train[['SPX_W']]
### 評価データを説明変数と目的変数に分割
X_testA = df_test[['TNX_W','DXY_W','OIL_W','GOLD_W','DXY_M','OIL_M','GOLD_M']]
y_testA = df_test[['SPX_W']]
## 予測実施
model.fit(X_trainA,y_trainA)
model.score(X_trainA,y_trainA)
predA = model.predict(X_testA)
model.score(X_testA,y_testA)
## 結果の可視化
fig = plt.figure(figsize = (30,10),facecolor="skyblue", tight_layout=True)
x1 = y_trainA.index
x2 = y_testA.index
y2 = y_test
y3 = predA
plt.grid(True)
plt.plot(x1,y1,color='k',label='Train Data')
plt.plot(x2,y2,color='r',label='Test Data')
plt.plot(x2,y3,color='b',label='Pred Data')
plt.legend()
plt.show()実行結果は下記となりました。


各々の決定係数を見てみると、学習データの決定係数は0.6近くなっており、まずまずの結果となりました。予測データの決定係数は依然に低いままですが、改善はみられています。
パターン①の結果から「説明変数に時間軸のデータを増やすことで、予測の精度の向上が見られた」と言えます。
これは月次差分、すなわち1ヶ月の価格変動データが学習の向上に寄与したことを意味しています。
ここで改めてパターン①で実施したことを図8. 説明変数の時間軸追加にてイメージ化しました。

説明変数として用いた米国10年債券、ドルインデックス、米国石油、米国ゴールド価格の値動きを1週間分の損益(週次差分)の他に、1ヶ月分の損益(月次差分)も追加したことになります。
ここで大事なのは、説明変数の種類を増やしたわけではなく、時間軸、即ち投資期間の差を用いていることです。
言い換えると、「1週間後の株価を予測するために、1週間分の増減結果を見るだけでなく、1ヶ月分の増減結果みて、予測をしている」と言えます。
この文章だけ見ても意味ありそうな感じはしますね。それがそのまま数字の結果として幾分か出てきたということと捉えています。
パターン②
### 学習データを説明変数と目的変数に分割
X_trainB = df_train[['TNX_W','DXY_W','OIL_W','GOLD_W','NASDAQ_W','DJI_W','DXY_M','OIL_M','GOLD_M','NASDAQ_M','DJI_M']]
y_trainB = df_train[['SPX_W']]
### 評価データを説明変数と目的変数に分割
X_testB = df_test[['TNX_W','DXY_W','OIL_W','GOLD_W','NASDAQ_W','DJI_W','DXY_M','OIL_M','GOLD_M','NASDAQ_M','DJI_M']]
y_testB = df_test[['SPX_W']]
## 予測実施
model.fit(X_trainB,y_trainB)
model.score(X_trainB,y_trainB)
predB = model.predict(X_testB)
model.score(X_testB,y_testB)
## 結果の可視化
fig = plt.figure(figsize = (30,10),facecolor="skyblue", tight_layout=True)
x1 = y_trainB.index
x2 = y_testB.index
y2 = y_test
y3 = predB
plt.grid(True)
plt.plot(x1,y1,color='k',label='Train Data')
plt.plot(x2,y2,color='r',label='Test Data')
plt.plot(x2,y3,color='b',label='Pred Data')
plt.legend()
plt.show()実行結果は下記となりました。


パターン①同様に、結果を見ていくと、決定係数が著しく向上し、学習データと予測データ共に、1に近い数値になっています。
これは、S&P500に連動性の高い(ほとんどの銘柄が包括されているため)ナスダック100およびダウ平均のデータが結果に寄与していると考えられます。
では、実際にS&P500の組み入れ銘柄がナスダック100およびダウ平均の組み入れ銘柄とどれだけ重複しているか確認してみましょう。
【米国株式インデックス投資ならどれ?徹底比較】(著:PayPayアセットマネジメント株式会社)が2021年6月末でまとめた情報によると、ダウ平均は30銘柄のすべて、ナスダック100は100銘柄のうち80銘柄がS&P500に含まれています。包含率80~100%の数値となっていることが分かります。
つまり、100%包含されているダウ平均の価格が上昇すれば、S&P500の価格も上昇する可能性が高くなるということが言えます。(ナスダック100も同様)
では、実際にこれらの指数がどれだけ関連性があるか相関係数で見ていましょう。
今回はSeabornライブラリを用いて、ヒートマップを作成しています。

ヒートマップでの縦と横が重なり合った青色の部分が相関係数です。
週次差分データとなる1週間分の損益は、統計的に強い正の相関にあり、1ヶ月分の損益は、正の相関があることが分かります。
相関係数は、2つの指標の関係性の強さを示す指標となるため、今回の結果で言い換えると、「S&P500とナスダック100、S&P500とダウ平均はそれぞれ、関係性がかなり強い」ということができます。
これらの結果からナスダック100およびダウ平均の価格変動データを説明変数に加えると、決定係数が著しく上昇したことには納得がいくかと思います。
8. 投資シミュレーション
最後に、モデルチューニング前(パターン⓪とする)、パターン①、パターン②の予測結果を利用して、実際に投資を行っていたと仮定してそれぞれいくら利益が出たか計算してみたいと思います。
前提条件は下記の通りです。
a) 予測結果の週次差分が0よりも大きい週を投資対象とする
b) 売買結果は週次差分の数値をそのまま利用する
c) 年末年始も投資対象とする(売買自体は可能なため)
d) 購入数は1株とする
e) ドル円の相場変動は考慮しない(1$=140円固定とする)
前提条件として、主にb)は当週終値 - 前週終値となるため、非現実的ですが、近しい結果は得られるため、今回は考慮しない。
それでは、実施してみましょう。
## 投資結果 パターン⓪
df_profit = df_all_w['2021-01-01':]
df_profit['PRED'] = pred
df_spx_profit.query('PRED > 0').sum()
## 投資結果 パターン①
df_profit['PRED_A'] = predA
df_spx_profit.query('PRED_A > 0').sum()
## 投資結果 パターン②
df_profit['PRED_B'] = predB
df_spx_profit.query('PRED_B > 0').sum()
パターン⓪とパターン①では106.7%増、パターン⓪とパターン②では147.6%増という結果となりました。
週次利益はどのパターンでも変わらないため、単純に投資機会の増加が要因となります。
9. まとめ
今回の分析では基本となる線形回帰分析で株価の予測を行いましたが、ナスダック100およびダウ平均の2種の株価指標を含めずに予測を行った場合、有意義な結果は出ませんでしたが、投資結果としてはまずまずの結果となることが分かりました。
また、説明変数に時間軸を追加した場合は予測精度の向上が見られました。
本分析だけでは、投資利用の信頼性は少ないですが、他の機械学習手法を用いた分析も実施し、投資利用価値の向上に努めたいと思います。
