
A coordinate-based colocalization (CBC) analysis
Single-Molecule Co-Localization Analysis
原理
CBC analysisは、STORM/PALMといった1分子画像の2種(2色)の分子間の共局在性を定量するのに使われる。相手(異色)との共局在の程度を、すべての点で算出する。定量は3つのステップからなる。第1のステップでは、任意の1点について、同種(同色、A)の距離の分布関数を計算する(下図)。

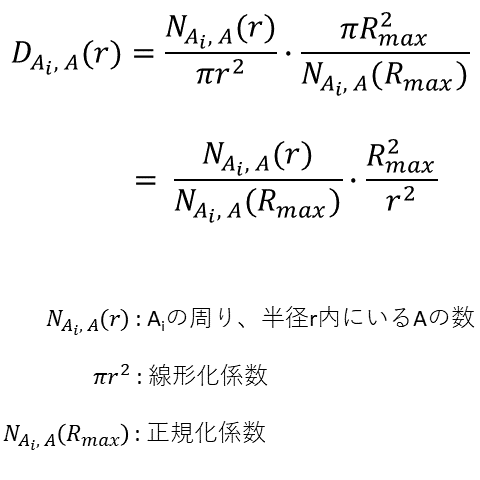
同種(A)との距離の分布関数は、観察された最大の距離(Rmax)の分布関数で正規化されることに注意。もし、同種の分子の分布が一様分布であればD(r)=1となる。
同様に、異種(異色、B)の距離の分布関数も計算する(下図)。

第2のステップでは、この異種・同種の2つの分布関数から、スピアマンの順位相関係数を計算する(下図)。

相関係数の分母は必ず>0の値になる。分子は、正、負、0のすべての値を取りうる。例えば、ある区間(rj)で同種の分子の数がすべての区間の平均よりも多く、かつ異種の分子の数も平均よりも多い状況であれば、分子は正の値を取る。同種、異種ともに平均よりも少ない場合も負✕負=正となる。逆に、同種の数が平均よりも多いが、異種の数が平均よりも少ない場合、分子の値は負の値になる。これによって、相関係数自体は-1から1の間の値を取る。値が大きいほど相関性が高く、共局在性が高いことを示している。
最後の第3のステップでは、この相関係数を距離分布で重み付けする(下図)。これは、外れの点で相関係数が、過大評価されるのを防ぐためである(to avoid long-distance effects)。

EAi, Bは任意の1点Aiからもっとも近い異種・異色の点までの距離。一般的には、Rmaxは回折限界以下の値を入力する。こうして得られたC値が任意の点Aiの異種分子Bとの共局在性の指標となる。同様に、任意の点Biの異種分子AとのC値も求める(下図)ので、すべての点(分子)についてC値が算出され、共局在の度合いが可視化される。

参考文献・サイト
Lama: The LocAlization Microscopy Analyzer
