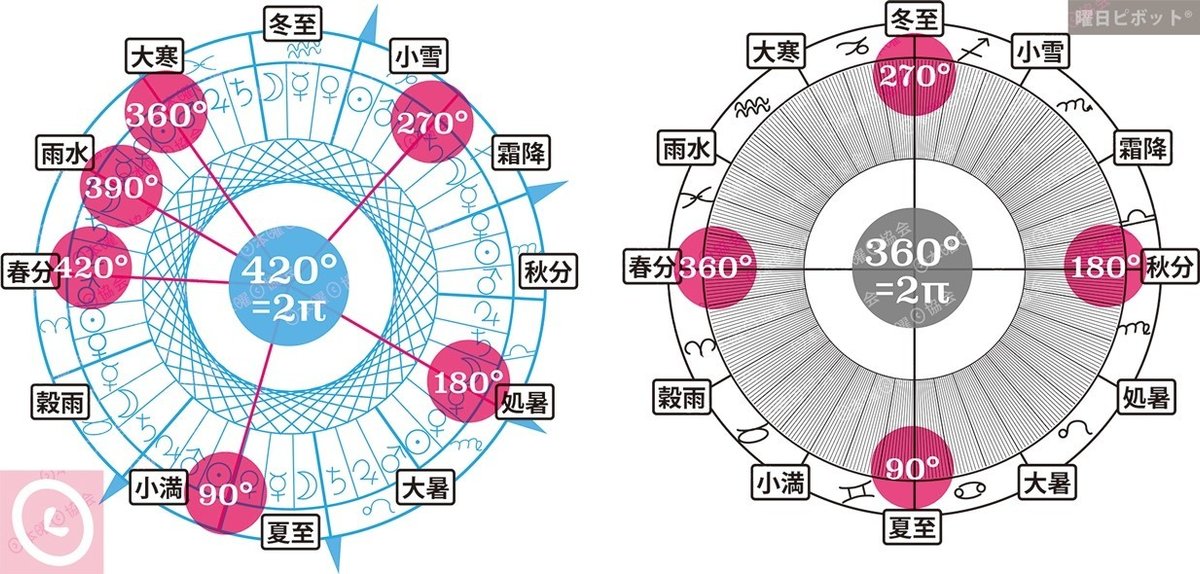
ポータルな度数と2π=420°=♡による時間の6つの相

360°の円を４分割すると直角：90°になります。
4つの度数は、90°、180°、270°、360°となり、二十四節気ではそれぞれ夏至、秋分、冬至、春分に該当します。四季の節目となる角度です。

420°の円では、この4つの度数は直角ではなくなります。二十四節気とも一致しなくなりますが、2π=420°=♡を実現するポータルな度数として重要です。

420°の円では、90°、180°、270°、360°に390°が加わり、180°と直線で結ばれます（オポジション）。

これら5つの度数の位置で折ると、2π=420°=♡は実現します。詳しい折り方の解説は、『2π=420°=♡ vol.1 -曜日の無限循環ゲーム』を参照してください。折り紙のテンプレートはこちらで配布しています。

2π=420°=♡は、桃を半分に切った形状に似ています。
半分の桃によって、時間の６つの相はイメージできます。

AとBは、桃の皮にあたります。
皮を剥くと実が現れます。皮の裏面あるいは実の表面がCとDにあたります。
中身の種子殻はEとFにあたります。

90°、270°、390°と、180°、360°、420°は、同じ位置で重なるので、A~Fのどの相にも移行できるポータルな度数となります。

これら6つの時間の相の詳細については次回解説します。