測量士補資格試験における基線解析とベクトル

令和３年度測量士補試験No.8
基線解析

２地点BとCとの間の距離を求める

実質的に空間ベクトルの成分表示です。
本問では、２地点BとCとの間の距離を求めます。
数学的には、
$${\overrightarrow{AB}}$$と$${\overrightarrow{AC}}$$から、
$${\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}}$$
により、
$${\overrightarrow{BC}}$$の成分を求め、
$${\sqrt{x成分^2+y成分^2+z成分^2}}$$
により、２点間距離を求めます。

高校生に対して指導する場合、実業高校の生徒は数学Bを履修していないケースも見られます。
そこで、上記の問題では＜Aを原点とみなす＞ことにより、ベクトル的に捉えずに２点間距離によって解決する指導も考えられます。

しかし、その場合には、以下の２問で問題が発生します。
令和５年度測量士補試験No.8

２地点BとCとの間の距離を求める

令和４年度測量士補試験No.9

基準点Bから基準点Cまでの基線ベクトルの成分を求める

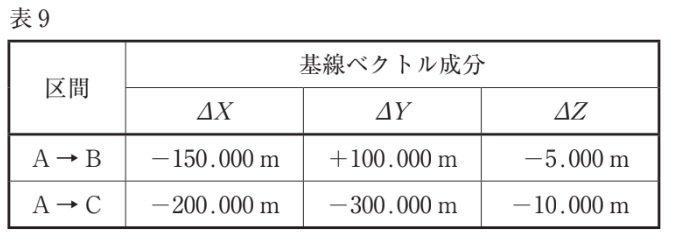
令和５年度では、
$${\overrightarrow{AB}}$$と$${\overrightarrow{CB}}$$が与えられています。
ベクトルを既習であれば、逆ベクトルの考え方で単純に符号を反対にするだけで令和３年度に帰着できますが、単なる座標ととらえていると、
「符号を反対にする」という発想をその場で思いつくのはややハードルがあります。

令和４年度では、距離ではなく、基線ベクトルの成分が聞かれています。
これも、ベクトルを既習であれば、
$${\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}}$$
によって求められるため、令和３年度よりも簡単な問題といえます。
しかし、距離を考える際には、ベクトルの向きを考える必要が
ないのに対して、成分の場合は、CからBを引く、という、
引き算の方向を考える必要があり、ベクトルを未習の生徒には
難しかったかもしれません。

令和６年度ではこのような出題はなされていませんが、
令和３年度から少しずつ形を変えて令和４年、令和５年と
出題されていることを考えると、たとえベクトルを授業で未習であっても、
・ベクトルの成分計算
・成分表示されたベクトルの距離の求め方
の２点を端的に指導した上で過去問に取り組ませた方がよいでしょう。

なお、上位資格である測量士試験でもこのようなベクトルの問題は出題されています。
国際地球基準座標系（ITRF：地球の重心を原点とし、短軸（北極方向）をZ軸の正、経度０度と赤道の交点方向をX軸の正、東経９０度と赤道の交点方向をY軸の正とする）において、九州から北海道へ向かうベクトルを成分表示した際の各成分の正負が、令和２年度午前試験のNo２にて聞かれています。