角を判定するロジック

お絵かきツールで作成するデータ「線」。
ペンやマウスでさっと画面をなぞれば一本の線ができあがる。
実に簡単な仕組みだ。
ところでその線とはつまり点の集まりである。

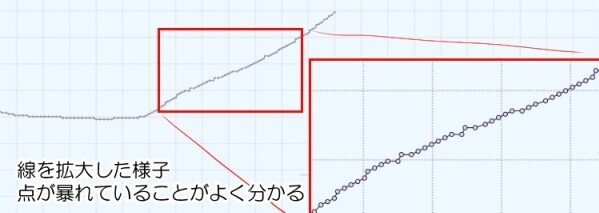
そして上図のように手書きの線は非常に汚い。
百戦錬磨の達人なら空気を切り裂く真剣のように正確無比の軌跡を描くことができるが、凡人には無理だ。
それをテクノロジーの力で手軽に実現できるようにしたい（それがこのツールの理念である）。

先ほどのガタガタの線をテクノロジーの力で点を平均化した。株をやっている向きには「移動平均線」でおなじみのワザだ。
手書きでは得られない美しく伸びやかな線がわが手に･･･。
めでたしめでたし。
・・・ではないのだ。

角が丸まってしまう！

そう、角が丸まってしまうのだ。
当たり前と言えば当たり前だがこれが非常に困る。

EXCELのシェイプをご覧いただきたい。
これはスプラインなので角の概念があり、角を鋭角に美しく描画することができる。
だが、左のシェイプでは角が丸まっている。
つまり角を角と認識できなければ望みの絵は描けないのだ。
（描けないことはないがここでは描けないものとして話を進める）
さぁ。角を角と認識しようか。

角を認識するロジック

状況を整理しよう
・線を滑らかにしたい。平均化制御は必ず施工する。
・ただし「角」は維持したい。
・というか平均化以前に「角」を認識しなければそもそも「角」処理ができない。
・「角」扱いにする角度は、30°。それ以上の折れ方であれば角と判定する

案１：全ての角度を調べる

A-BとB-Cの角度を比較し、差が30°以上あれば角。実に簡単だ。
・・・というわけじゃないんだこれが

案２：外接を調べる

角は尖ってるのだから、他より外側にあるんじゃね？という切り口。
線形状に接する四角を描き、角を検知したらそれが一番”外側”にあるかどうかを調べる。「30°以上」かつ「最外」なら「角」だ。

そんなわけなかった😫

案３：細かい四角で線形状を区切る

全体を一括するんじゃなくて細かく区切れば内向き角も拾えるでしょ？という考え方。

無意味だった😫

案４：スピードを見る

線を描くときの速度を見る。
角を作る際は必ず0スピードになる。その瞬間を拾えばいい。
俺は天才か･･･！

天才じゃなかった(´・ω・｀)

案５：作画中にキー入力でマークする

そんなメンドクサイツールまず俺が使わん

そもそも人はどうやって角を角と認識するのか

点の一個一個を見てもそこに角の成否を決める情報はない。言ってみれば全部角だ。
だが、我々はこの図形を見て「ここが角だ」と判別できる。
それは何故だ？

いや！

そうだ！
A-B,B-Cの流れじゃなくて、点を中心としたB-A、B-Cの成す角で考えるんだ！

点を中心に遠くの前後を見るという発想

というわけでその理論を検証するプログラムを組んでみた
（「ベクトルの差分」ではなく「角の角度」なので閾値は30°ではなく150°とする）

思ったよりもうまくいった
「遠くを見る」方法は「線上の距離」の累積で算出しているが、点の配置が均等なので「ID」で検索しても問題ないだろう。
角付近の「腕」の動きが特徴的で面白い。
この「腕」の縮まり方という情報も何かしら役に立ちそうだ。

長い線でもこの通り。
俺は天才じゃないか･･･？

いやー、「線」という概念に捉われすぎてた。イカンイカン。
よくよく考えたら昔、同じ理論でポリゴンのエッジを保持したままサブディバイドするスクリプト書いてたわ(ﾟ∀ﾟ)ｱﾋｬ