
時間的光理論「光速差から生成される局所慣性(ガリレイ)系」
「ひゃまの飛んでもない光論」というと無矛盾や新規性を求めて研究色が強いので、その研究から出た成果の時間的光理論(Temporal Light Theory)はまともだと自負しているので、他の理論体系での位置づけをしておこうと思う。
1、特殊相対論や電磁気学との関係
古典力学で用いられている、ひとつの慣性系から他の慣性系に移るときの、事象の二組の空間座標と時刻の関係規則によると、二つの仮定(1)光速度一定(2)法則が(したがって光速度一定の法則も)慣性系の選択と無関係であること(特殊相対性原理)は(両者がそれぞれ経験によって支持されているという事実にもか.かわらず)互いに両立しない。
要は、この(1)の電磁気学からの要請と、(2)のSRの第一原理である相対性原理を満たせば、第二原理である光速度不変の原理に拘らないということらしい。これは本来、異なる系間を相対させるべきなのだが、その系間の境界を無境界にして運動する物体間の古典の相対性を引き摺り辻褄合わせしてしまったため、アインシュタインも死ぬまで懸念しており、これが本当の意味でアインシュタインの最後の宿題とも考えられる。
まず、上のように特徴づけられる、この理論についてひとつの注意をする。この理論が(四次元空間を別にして)二種類の物理的なもの、すなわち(1)測定棒と時計、(2)例えぱ電磁場や物質点などの他のすべてのものを導入するという事実は奇異の感をいだかせる。これはある意味では矛盾している。厳密にいうと、測定棒と時計はあたかも理論的に自明なものとしてではなく、基本方程式の解(運動している原子の配位からなる対象物)として表わされなければならないであろう。しかしながら、そもそもの始めから、理論の仮定が、そこから物理的事象の十分に完全な方程式を十分任意性のないように導くことができ、そこに測定棒と時計の理論を基礎づげることができるほどしっかりしてはいないのであるから、この手続きは正当である。
座標の物理的解釈を(それ自身可能な何かを)一般にあきらめたくないならば、このような矛盾を許すほうがよいが----もちろん、理論の以後の研究において、それを取り除く必要はある。しかし、ここに述べた欠点を正当化して、距離を、他の物理的な量と本質的に異なる、特別な物理的実体であると想像すべきではない(“物理学を幾何学に還元する”など)。
この第二原理を光の運動量の等価原理にすれば、パラドックスのない関係になる。
※¹ 折り合う条件:光速度不変の原理を止めること
2、一般相対論や宇宙論との関係
そもそも特殊が先というだけで、重力を考慮してない力学はありえない。重力質量と慣性質量の関係を「光速度不変の原理」の代わりに据えた「光の運動量の等価原理」は含んでいるので、水星の近日点移動もニュートン力学の正当な拡張で特異点などなく対応可能である。
空間が湾曲すると干渉計のアームと光波が同じように変化するため、時間変動の波(重力波)を検出できない。
これも光速の変化=時間の遅れを、時空連続体の変化に挿げ替えているだけだ。
※² 折り合う条件:時空連続体を止めること
3、量子論や量子力学との関係
SRやGRの第一原理である相対性原理を、プランク定数を含む「量子論のための相対性原理」にすれば、DSLは、
(1) 量子論のための相対性原理
(2) 光の運動量の等価原理
この二つの原理を据えることになる。
そもそも量子力学の不確定性原理は、
運動量やエネルギーでなくて、時間を含まない不確定性関係にする必要がある。
h / c = δm δλ (kg・m) (1)
式 (1) に時間を入れると光の運動量やエネルギーが確定し、光の運動量の等価原理とリンクする。
p = h f / c = m f λ = m w = M c (kg・m/s) (2)
※³ 折り合う条件:不確定性関係に時間単位の要素を止めること
4、万物理論やスケーリング理論との関係
そもそも光速度不変の原理やアインシュタインの等価原理のスキーム(m=M、w=c)では、質量と波長の関係を古典に縛り付けるだけで、式(1)の量子論のための相対性原理であれば、エネルギーの変化は重力質量の変化、スケールの変化は慣性質量の変化と分けたらよいだけである。
※⁴ 折り合う条件:質量の等価原理を止めること
5、ニュートン力学や古典力学との関係
考え方の違いは光速度を基準にするなら静止している波動などないので、「物体の動かしにくさ」という物質単位の質量の定義から、「静止質量は粒子の種類によらず重力質量と慣性質量が同じ静止系では同じになる質量」へ、ニュートン力学を正しく拡張すればよい。
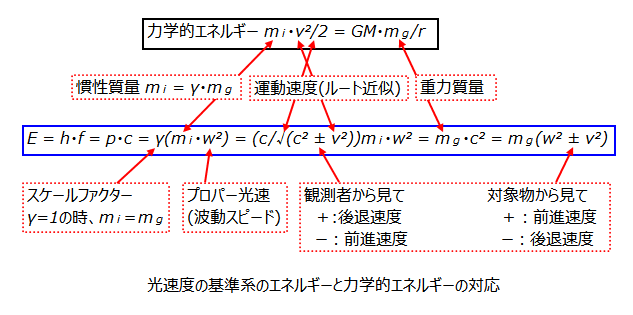
基本粒子であるか複合粒子であるかなど粒子種で分類済みであり、それ以上にエネルギーや光の運動量を質量の有無で分ける必要はないが、系間の境界を無境界にし光速度不変に時空連続体を優先した結果、質量殻を持つ物質粒子以外の粒子に質量はないという問題に挿げ替えているだけだ。
これ以外の慣性質量や重力質量 は そ れ こ そ 混乱 の もと とな る の で使わ な い こ とに し よ う と提 唱 して い る。
※⁵ 折り合う条件:質量殻の質量の定義を止めること
折り合いのまとめ
※¹:光速度不変の原理を止める。
※²:時空連続体を止める。
※³:不確定性関係に時間単位の要素を止める。
※⁴:質量の等価原理を止める。
※⁵ 質量殻の質量の定義を止める。
これらは互いに連動しており、古典物理学の慣習を引き摺って時空連続体に押し付けた結果であり、当のアインシュタインですら以下のように述べている。
物理的に重要なのは系間の相対性であり、その境界を無境界にして幾何学で数学をすることではないので、本格的な物理理論のパラダイムはシフトされておらず、古典的慣習を止めると本格的なパラダイムシフトによる成果が期待できる。
