
後退する宇宙の相対レートによる光時間階層論
著者の所属機関
Hyama Natural Science Research Institute
キーワード
相対時間, 宇宙の階層構造, 観測基準系, 光でドップラー効果, 階層性, 時間階層, 未解決問題, フライバイアノマリー, 階層性問題, 相対速度因子, 光の運動量, 等価原理, 近日点移動, 銀河, ダークマター.
要旨
絶対静止座標系を廃し相対性理論を提唱したアインシュタインは, 遠くの銀河が後退するのを知り, 静的宇宙を諦めた.私たちは、彼の相対性理論のおかげで絶対時間から解放された反面、宇宙の階層構造における相対時間の階層性問題が浮上し, 多くのパラドックスと未解決問題を残している.本論は, ニュートン力学以前のガリレイ不変性まで立ち返り, ”相対速度変換の下の階層性と光の運動量の等価原理”によって, 後退する宇宙の時間階層における相対性の幾つかのパラドックスと未解決問題を解明する.
1. イントロダクション
ガリレイ不変性を, 絶対静止座標系を前提にガリレイ変換を定式化したニュートン力学だが, 電磁気学との不整合により絶対静止座標系を廃し, ローレンツ変換によるアインシュタイン(1905)[1]の特殊相対性理論(SR)が誕生した.しかしアインシュタイン(1947)[2]は「座標の物理的解釈を(それ自身可能な何かを)一般にあきらめたくないならば, このような矛盾を許すほうがよいが----もちろん, 理論の以後の研究において, それを取り除く必要がある.」と言っている. 働いている力の和(合力)が 0 である物体がする運動を慣性運動といい, 慣性系はその慣性運動と, それと共に運動する時計と物差しで測る時間と空間をひとまとめにした概念である.したがって時間の速さが異なる慣性系間では, 2乗3乗則を加味しないといけないが, ローレンツ変換ではそれが定義できていない.また, その舞台である大域的慣性系も後退する宇宙に即して定義できてない.本論は, それらを加味した後退する宇宙の大域的な慣性系と, 宇宙の階層構造におけるスケール変換を見直し, 「後退する宇宙の相対レートによる階層性力学」について説明する.
2. 相対運動を相対時間で定義
絶対静止基準の相対運動には, ±がある.
相対速度(v±) = 対象の運動速度(vb) - 観測者の運動速度(va). (1)
それを排除し, 光の速さを観測基準にした相対運動にも, ±がある.
運動速度(v±)² = 対象の固有光速(w±)² - 観測者の不変光速(c)²,
w₊ > c の場合は, v₊:後退速度, w₋ < c の場合は,v₋:前進速度. (2)
これは, 手動で座標変換しなくとも, 対象の固有光速と運動速度の境界面で干渉して, 自動で不変光速な観測基準系が生成される.
c² = w² ± v². (3)
つまり階層性から不変系が生成されているのが, ガリレイ不変性が言うところである. したがって絶対時間の縛りがない時間は,「ある固有光速」中の振動数から単位を作ってるだけなので, その「ある固有光速」を不変光速とするなら, その固有光速が相対時間の速さである.絶対静止座標系の背景を排除して残った相対時間を, 時間と空間を同等に扱う時空の背景で縛っては, 背景独立性を失うことになる.
相対速度因子 γ = c / w = c / (c² ± v²)¹ᐟ², τ = γ t, x = c t = w τ,
t:観測者の経過時間, τ:対象の経過時間, x:距離. (4)
対象の固有光速が遅い場合(c > w₋), 距離(x)を進むのに経過時間(τ)が掛かる.
対象の固有光速が速い場合(c < w₊), 距離(x)を進むのに経過時間(τ)が掛からない.
それを不変光速(c)を定義値で固定して時空や物の長さが変化させてしまうと, 加速により速さと時間と距離の関係が破れるか, ベルの宇宙船パラドックスのように3体間でローレンツ対称性が破れてしまう.
例えば, GPS衛星に搭載された原子時計と地表の時計の進み方の比は,
地表の不変光速(c): 299,792,458 m/s.
地心重力定数(GM): 3.986e + 14 m³/s².
地球半径(r): 6,378,000 m.
無限遠の固有光速, w∞ = (c² + 2GM / r)¹ᐟ².
GPS衛星の高度(h): 20,200,000 m.
GPS衛星の軌道速度(v): 3,874 m/s.
GPS衛星の固有光速, w₉ = (w∞² - 2GM /[r + h] - v²)¹ᐟ².
光時計の相対レート, 1 / γ₉ = w₉ / c = 1 + 4.45e-10.
3. 宇宙の時間の減速と観測基準系

この観測基準系から遠くの銀河をみると, 宇宙論的赤方偏移から換算した後退速度が観測される.これを観測者の時間の減速と考え, 宇宙の時間が減速しているとする.アインシュタイン(1905)は時間の速さが変化する境界条件を無くし, 同時の相対性からが導いた前進速度だけのローレンツ対称なSRを導いた.しかしながら前進速度だけのローレンツ対称で起きる”時間の遅れはお互い様”な現象が, 宇宙の時間の減速により, 遠くの銀河の観測者同士から見た後退速度で起きるでしょう.また”双子のパラドックスも, 前進速度を増した兄弟の宇宙の時間がより減速することで, 観測可能な宇宙の中で解決する.
4. 光のドップラー効果の非対称性
相対時間だけでは, 階層な運動速度が予め分かっている訳ではないので, プライマリードップラー効果だけでなく, 光特有のセカンダリドップラー効果も階層なドップラー効果を準備する必要がある.

4-1. 光源は観察者より時間のスピードが遅い(c > w₋)
光源の固有光速(w₋)は,
γ₊ = 1 / γ₋ = c / w₊, w₋ = γ₊ c = (c² - v₋²)¹ᐟ²,
v₋ = c (1 - γ₊²)¹ᐟ²= (c² - w₋²)¹ᐟ². (5)
光源で発生する二次ドップラー周波数(f₋)は,
γ₋ = 1 / γ₊ = c / w₋, f₋ = f₀ / γ₋,
f±:二次ドップラー周波数, f₀:基準周波数. (6)
光源から光を放出すると境界面で, 二次ドップラー波長(λ₋)は,
λ₋ = γ₋ λ₀, λ± :二次ドップラー波長, λ₀:基準波長. (7)
観測者から見た角度(θ)の方向の光源が前進速度(v₋)で運動している場合, 観測周波数(f)と観測波長(λ)は,
β = v₋ / c, f = f₋ / (1 - β cos θ), λ = c / f,
β : 運動光速比, θ:観察者から見た光源の角度.(8)
4-2. 観察者は光源より時間のスピードが遅い(c < w₊)
光源の固有光速(w₊)は,
w₊ = γ₋ c = (c² + v₊²)¹ᐟ², v₊ = c (γ₋² - 1)¹ᐟ²= (w₊² - c²)¹ᐟ². (9)
光源で発生する二次ドップラー周波数は,
f₊ = f₀ / γ₊. (10)
観測者の境界面に入射する際, 二次ドップラー波長(λ₊)は,
λ₊ = γ₊ λ₀. (11)
光源が観測者から見た角度(θ)の方向に後退速度(v₊)で運動している場合, 観測周波数(f)と観測波長(λ)は,
β = v₊ / w₊, f = f₊ / (1 - β cos θ), λ = c / f. (12)
4-3. 未解決のフライバイ・アノマリー
例えば, 未解決問題であるフライバイアノマリーでは, ある緯度(φ)にあるディープスペースネットワーク(DSN)から見た, 地球フライバイする探査機から伝搬してくる固有光速は, 地球の自転速度(ω R)してない分, 二次ドップラーシフトにより超光速(c < w₊)になる.
w₊ = (c² + [ω R cos φ]²)¹ᐟ². (13)
そのため(式8)と(式12)の違いである光路の光速差(c < w₊)がプライマリードップラー周波数差(⊿f₊)として, 無限遠での速度増分(フライバイアノマリー:⊿v₊∞)に現れる.
⊿f₊ / f = (f₊ - f ) / f = ⊿v₊∞ cos θ / c. (14)
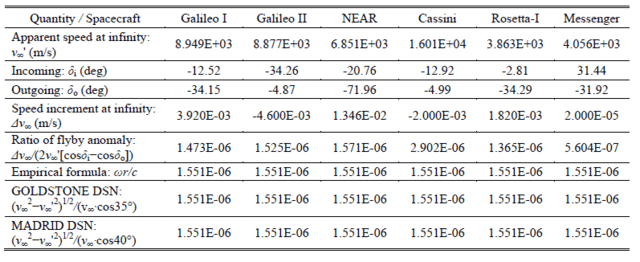
⊿V∞/(2 V∞’[cos δi-cos δo])=ω R/c=√(V∞²-V∞'²)/(V∞ cos θ)
アインシュタイン(1905)[1]は, どちらがより動いているか分からないのでアインシュタイン同期に頼ったが, 彼が光伝搬の簡単に検証可能な物理的特性に還元できることを知らなかった.したがって, このアノマリーはV. Guruprasad(2015)[3]が言うように, 光でドップラー効果の対称性に係るSRの問題と言える.
5. 宇宙の時間階層における階層性問題
5-1. スケール効果と, 光の運動量の等価原理
ニュートン力学では, 密度とは単位体積あたりの質量のことを指し, 物質密度=質量/体積という変換式によって表現できる.その物質密度を電磁波の運動量密度まで広げて光の運動量(p)に換算すると, エネルギー(E)との関係は,
E = c |p|. (15)
それにガリレイの等価原理(自由落下の一般性)を要請すると, ニュートン力学の重力質量(m₉ = E / c²)のエネルギーの大きさや増減と, 運動による慣性質量(mi = γ m₉)の相対速度変化は, 無関係であると訳せる.
|p| = m₉ c = mi w, E = m₉ c² = γ mi w². (16)
つまり(静止質量:m₀=mi=m₉)と(c=w₀)の場合だけ一つの慣性系であることが, アインシュタインの等価原理に一致する. これをHamaji(2013)[4]の光の運動量の等価原理という.この重力質量と慣性質量の違いは時間の速さの違いと等価であるからスケール効果が発生して, 宇宙の時間階層において逆2乗の法則からのズレを産む.
✖ 絶対時間 ⇒ 逆2乗則.
↓
〇 相対時間 ⇒ 2乗3乗則.
5-2. 光の運動量の等価原理と, 近日点移動誤差
太陽系惑星の近日点移動は, 他の惑星からのニュートン力学による重力の摂動でほとんど説明できる.例えば水星が100年間で起こす近日点移動575″のうち , 他の惑星からの重力の影響は, ニュートン力学で計算すると計532″となり全体の90%以上となるとされている.Will, Clifford(2011)[5]は, 1915年にアインシュタインが測地線方程式と太陽の周りの時空計量の近似解を使用して, 水星の近日移動への相対論的寄与と観測を一致させることができたことを言っている. ニュートン力学の遠心力と万有引力のつり合い式は,
GM☉ m₉ / r² - mi v₋² / r = 0,
GM☉:日心重力定数, r:惑星と太陽との距離. (17)
不変光速(c)の観測基準系を無限遠へおいて, (式17)から(式16)の光の運動量の等価原理を用いて惑星の質量を消去すると,
γ₋ v² = GM☉ / r, γ₋ = c / w₋ = 1 / (1 - v₋² / c²)¹ᐟ². (18)
(式18)の(v₋ = 2π r / T)に置き換えてKeplerの第3法則で表現すると,
4 π² γ₋ = GM☉ T² / r³, T:惑星の公転周期. (19)
(式19)の左辺から公転する一周回の誤差(⊿φ)は,
⊿φ = 4 π² (γ₋ - 1). (20)
(式20)から水星の100 年で415周回の秒角(x”)は,
x″ = ⊿φ (180 / π) × 3600 × 415. (21)
観測から軌道速度(v)と公転周期(T)が分かれば, 相対速度因子(γ)から絶対静止座標系を廃したニュートン力学で各惑星の近日点移動の厳密解が求まる.

アインシュタインは, ローレンツ変換 の下での対称性と光速度不変の原理を要請する事で, SRを作り出した.更に, 一般座標変換の下での対称性とアインシュタインの等価原理を要請して, 一般相対性理論(GR)という重力の理論を構築している.本論は, 相対速度変換の下の階層性と光の運動量の等価原理で, Galileiとニュートンの力学とアインシュタインの相対論の長所だけを踏襲している.
5-3. 銀河の回転曲線問題とダークマター
以上で, 系間の時間の速さの違いによる慣性運動の逆2乗則からのズレを見てきたが, 銀河群と銀河の関係においてはもっと顕著化する.銀河群は, 最小の銀河の集まりである.銀河の数は50を超えず, 典型的には直径は1-2Mpc, 質量は約10¹³太陽質量である.ここの銀河の分散速度(v₊)は, 約150km/sである.このような銀河内部の観測基準系(c)から光の運動量の等価原理でみると, 距離 の逆数次元(m⁻¹)の後退係数(k₊)に置き換えた約10¹¹太陽質量以上の銀河の総質量(Mⓖ)から(式17)の力のつり合い式は,
w₊² - c² = v₊² = GMⓖ k₊. (22)
これは銀河が分散速度(v₊)で転がっているイメージで, (式22)を, 銀河の中心からの位置(r)内の質量(M[r])で書き直すと,
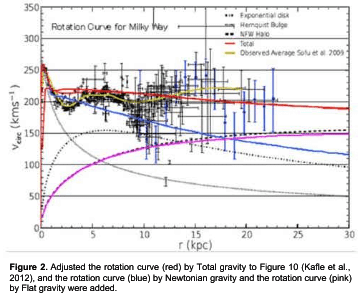
v(r)² = GM(r) / r + GM(r) k₊ = GM(r) (1 / r + k₊). (23)
(式23)の右辺の第1項はニュートンポテンシャル(1 / r)である. 第2項は(GM[r]→ GMⓖ)に漸近しながら増加するダークマターである. その合算により銀河内が回転(v[r] → v₊)する.
6. 結論
そもそもガリレイ不変性は, 宇宙の階層構造の各階層で不変性が起きる不思議を原理にしたものだ.それは系間の対称性が起きている訳でもないし, 相対時間の速さの違いにより発生するスケール効果は無視できない.絶対時間やローレンツ対称性の縛りがない相対時間の速さが変化して, 光速が変化しない現象はない.M. Senovillaら[8]は, そもそも宇宙は加速度的に膨張していないため, ダークエネルギーも必要ないと言っている.加速しているように見えるのは, 実は時間そのものが減速しているためであり, 今よりも時間経過が速かった過去の超新星爆発を観測したために起こった見かけ上の現象に過ぎないということだ.もしそうであれば, メートルに対して天文単位が増加しているようにみえる天文単位の永年増加や, 力学的モデルとは一致しないこの離心率のわずかな拡大の月の離心率の増大も, それと関係している.また本論で説明した宇宙の階層構造におけるパラドックスや未解決問題や, はたまた素粒子論の階層性問題も,「後退する宇宙の時間階層における波動相対性」で一層できる可能性がある.近年, 平衡状態では起こりえないと言われていた時間結晶も, 非平衡状態では追試で確認され, もはや未解決問題ではない.それと同じように対称な相対性を廃して, 階層性な相対性に見直した方が, 量子重力理論への近道ではないだろうか?
Authorship Contribution Statement
Competing Interests
The author declares there are no competing interests.
Acknowledgments
長年, 相対性理論の問題点について一緒に向き合ってくれたQ&Aサイトの皆様に感謝する.
参考文献
[1] Einstein, Albert. "On the electrodynamics of moving bodies." Annalen der physik 17.10 (1905): 891-921. https://www.fourmilab.ch/etexts/einstein/specrel/www/
[2] Einstein, Albert. (1947). "jiden nooto" Tokyo tosho(1978)p73~81 (fnorio.com)
[3] V. Guruprasad (2015), "Observational evidence for travelling wave modes bearing distance proportional shifts", EPL, 110 (5): 54001, arXiv:1507.08222, Bibcode:2015EL....11054001G, doi:10.1209/0295-5075/110/54001
[4] Hamaji, Shinsuke. "Equivalence principle of lights momentum harmonizing observation from quantum theory to cosmology." International Journal of Physical Sciences 8.38 (2013): 1885-1891. https://academicjournals.org/journal/IJPS/article-abstract/D20A5B441835
[5] Will, Clifford M. "On the unreasonable effectiveness of the post-Newtonian approximation in gravitational physics." Proceedings of the National Academy of Sciences 108.15 (2011): 5938-5945. https://www.pnas.org/doi/full/10.1073/pnas.1103127108
[6] Nobili, Anna M., and Clifford M. Will. "The real value of Mercury's perihelion advance." Nature 320.6057 (1986): 39-41. https://www.nature.com/articles/320039a0
[7] Hamaji, Shinsuke. "Flat gravity based on Hubbles law which expanded Newtonian gravity." International Journal of Physical Sciences 9.22 (2014): 487-494. https://academicjournals.org/journal/IJPS/article-abstract/98D1AAE48839
[8] Marc Mars, José M. M. Senovilla, Raül Vera. "Accelerating expansion and change of signature". arXiv:0712.1462
