
Proving the Collatz Conjecture Using Infinite Axiom and Proof by Contradiction(preprint)
In a previous attempt, the Collatz Conjecture was explored through Peano's axioms, but since induction doesn't satisfy the infinite range of natural numbers, let's demonstrate it using the Infinite Axiom and proof by contradiction, making it comprehensible to everyone. Each paragraph of the proof begins with the set of positive integers, goes through the classification of double sequences of odd numbers, the forms of odd numbers, the association of sequences, and the bottom-up process, and finally concludes that the Collatz conjecture holds.
1. Infinite Set of Positive Integers
As a premise, there exists an infinite set of positive integers. By defining subsets, we can distinguish the empty set {} from the set of natural numbers. This is in contrast with the notion of infinity and zero. The premise regarding the infinite set of positive integers can be expressed using the Infinity Axiom as follows:
Infinity Axiom: There exists a set x such that the empty set ∅ is an element of x, and for any y that is an element of x, S(y) is also an element of x.
2. Odd-Even Split of the Integers
We divide the integers into subsets of odd and even numbers. {1, 2, 4, 8, 16, ...} represents the sequence of odd numbers multiplied by 2. {3, 6, 12, 24, 32, ...} represents the sequence of even numbers divided by 2. This encompasses all even numbers under the Collatz calculation, leaving the connections between remaining odd numbers' sequences to the 3x+1 operation.
3.Odd Numbers: 4n+1 and 4m+3 Forms
Odd numbers are classified into two forms: 4n+1 and 4m+3. Examples of the forms include 4n+1: 1, 5, 9, 13, 17... and 4m+3: 3, 7, 11, 15, 19...
4. Organizing 4m+3 Sequences According to 4n+1 Sequences
For an odd number x=4m₁+3, applying 3x+1 yields 12m₁+10, then 6m₁+5. If m₁ is odd, 6m₁+5 becomes 4m₂+3 type odd number, for instance 7 (4(1)+3) and 11 (4(2)+3). If m₁ is even, 6m₁+5 becomes 4n+1 type odd number, for instance 11 (4(2)+3) and 17 (4(4)+1). Consequently, there's a link between 4m₁+3 type odd numbers and 4m₂+3 type odd numbers, leading to 4n+1 type odd numbers (where m=[n-1]/3 is an integer) which are twice the size of 4m+3 type odd numbers. This establishes a correspondence between 4n+1 type odd numbers' sequences and 4m+3 type odd numbers' sequences under the Collatz operation.
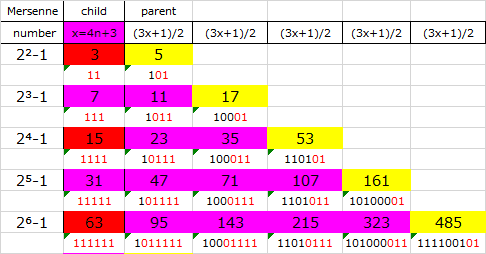
5. Defining 0th Generation as the Sequence 4(0)+1=1
{1, 2, (4), 8, (16), 32, (64), 128, (256), ...} represents the 4(3n+1)=12n+4 format, where numbers in parentheses indicate this format.
6. Mapping 0th Generation's 12n+4 Evens to 1st Generation's 4n+1 Odds
By subtracting 1 from 12n+4 and dividing by 3, we obtain 4n+1 type odd numbers. For example, 12(1)+4 becomes (16-1)/3 = 5 = 4(1)+1. These 4n+1 type odd numbers, except for n=0, become the 1st generation.

The injective relationship from one odd integer sequence to the next generation's odd integer sequence through the transformation 3n+1→4n+1, along with the connection between odd integer sequences of the subsequent generation through the equation 4n₂+1=4(4n₁+1)+1, is a rule that holds universally across all generations.
7. Bottom-Up Progression from 0th to 1st to 2nd Generation Links All 4n+1 Odd Number Subsets in a Tree Structure
Therefore, performing the Collatz operation on any positive integer results in each 1st generation containing a 4n+1 type odd number, forming a tree structure with these odd numbers as labels, leading to a loop of 4(0)+1=1, 2, 4 in the 0th generation.
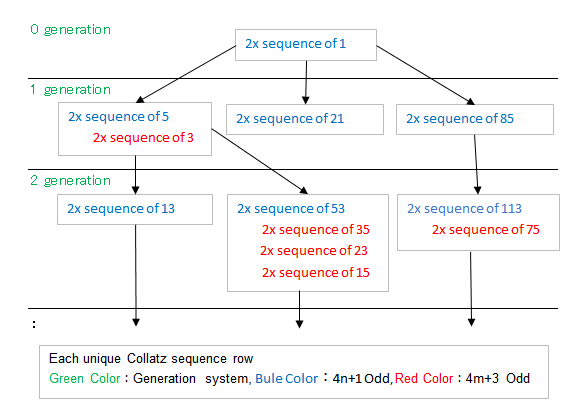
Conclusion
By establishing the one-to-one correspondence between 4n+1 and 3n+1, and demonstrating that under Collatz reverse calculation, only new subsets of 4n+1 are linked to the entrance of 4n+1's subsets, resulting in infinite divergence without loops, this, along with the connectivity between these aspects established through reductio ad absurdum, shows that when the sequence of 1's multiples is expanded infinitely, all 4n+1 type odd numbers connect in a tree structure. Thus, the Collatz Conjecture is shown to be explainable from the axioms of infinity and the properties of positive integers.

Additional Information
In this proof, we have demonstrated the validity of the weak Collatz conjecture, which asserts that every natural number reaches the value of 1 through a finite number of operations. However, the specific details regarding the exact number of steps and generations required to reach 1, as proposed by the strong Collatz conjecture, have not been addressed in this proof.
It is important to note that the strong Collatz conjecture, a mathematical problem of great complexity, remains unproven and represents a challenge within the current realm of mathematical knowledge. Ongoing research is dedicated to resolving this long-standing question. While this proof significantly advances our understanding of the weak Collatz conjecture, the pursuit of the strong Collatz conjecture necessitates further investigation.
