
重力赤方偏移パラドックス
相対論には2つの考えがあって、アインシュタインの特殊(SR)や一般(GR)相対論は時間と空間が共変すると、階層性相対論(HR)は時間と光速が共変する。 https://note.com/s_hyama/n/nb3a040bb74e0
観測者の不変光速(c)、伝搬してくる光速(w)、重力ポテンシャル(2GM/r)の関係は、
c²=w²+2GM/r・・・(1).
(w₉²=2GM//r₉)でシュバルトシルト半径(r₉)のブラックホールとして (r₉→無限遠方)で、(w₉→c)に光速が変化する。
w₉=f₉λ₉ → c=f₉λ・・・(2).
これは、周波数(f₉)は変わらず、波長が伸びて(λ₉→λ)光速が速く(w₉→c)共変するのが、重力赤方偏移ね。この時、光子のエネルギーは抜け出してくるエネルギーは変わらないのだけど、
E=hf₉・・・(3).
第三に,強い重力場をもつ天体からの光は,重力ポテンシャルを脱出するさいにエネルギーを失い赤方偏移を生じる。ここで「光」と表現をしているが,実際には電磁波に共通の現象で,相対性理論で理解できる。 https://www.s.u-tokyo.ac.jp/ja/story/newsletter/keywords/21/03.html
この一般相対論(GR)で重力場を光子が抜け出してくる時エネルギーを失い、重力場がエネルギーを持つと言う考え方は、光速度不変cから波長が(λ₉<λ)、周波数(f₉>f)になり、たしかに波長が伸びて赤方偏移するのだけど、GRは、もともとエネルギー保存に問題があるのでしょう。
c=f₉λ₉ → c=fλ・・・(4).
その理由は、重力と物質との関係を規定するアインシュタイン方程式において、物質のエネルギーと運動量を表すテンソルが通常の保存則を満たさないからで、アインシュタインは重力場に付随するテンソルに似た「擬テンソル」と呼ばれる量を考案。これを物質のエネルギー運動量テンソルに付け加えることで、保存量を構成できると指摘したのである。
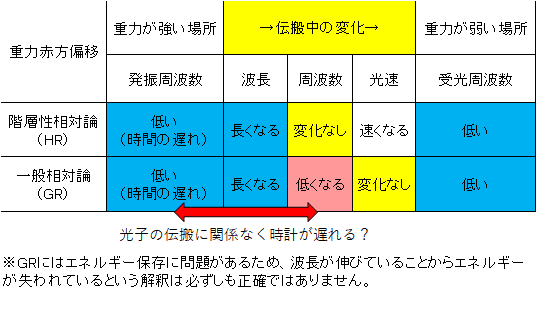
結論として、重力が強い場所では、光子が脱出するしないに関係なく、時間の進み方が遅れる=発振周波数が低くなるので、一般相対論の重力場で伝搬中に光子がエネルギーを失う=周波数が低くなるのは間違っています。
これと同じ原理で、反射する惑星間の距離は、電磁波との伝搬とは無関係であるので、距離が変わらず、波長と光速が共変するシャピロ遅延があります。
しかしこの場合は、太陽に近づくとエネルギーを貰い(周波数が高く)、遠ざかるとエネルギーを失う(周波数が低く)と言う言い訳が出来てしまうところが、重力赤方偏移と違うところで、重力赤方偏移は光の伝搬が無くても強い重力場では時計の進み方が遅れるのが原因でそんな言い訳が通じない。
時空の性質の結果として[2]、観測者に対して相対的に動いている時計は、観測者自身の基準系内で静止している時計よりも進み方が遅く、または早く観測される。また、観測者よりも強い重力場の影響を受けている時計も、観測者自身の時計より遅く、または早く観測される。いずれも静止している観測者や重力源から無限遠方の観測者を基準として、時計の進み方が「遅い」と表現される。 https://ja.wikipedia.org/wiki/%E6%99%82%E9%96%93%E3%81%AE%E9%81%85%E3%82%8C
