Title: "Proof of Goldbach's Conjecture from the Ratio of Primes and Composites (Preprint)"

Abstract:

In this paper, we calculate the relationship between the number of prime pairs and composite pairs from empirical measurements of the ratio of primes and composites. We also discuss the relationship between the number of prime pairs and composite pairs based on the Prime Number Theorem, demonstrating that Goldbach's conjecture holds true even in unexplored domains.

Introduction:

In 1742, Prussian mathematician Christian Goldbach wrote a letter to Leonhard Euler, stating that every natural number greater than 2 can be expressed as the sum of two prime numbers [1]. While this conjecture has been shown to hold for all integers below 4×10¹⁸ [2], it has remained unproven for nearly 300 years despite significant efforts. In this paper, we attempt to demonstrate the conjecture's validity by examining the ratio of primes and composites.

The Ratio of Primes to Composites:

Let's denote the number of prime numbers up to an even number n as "a", and the number of odd composite numbers as "b", which can be calculated as b = n/2 - a. The upper limit for the number of odd composite pairs that sum up to n is "c", where c = b/2, and the lower limit is given by c = (b - a)/2, assuming that all 'a' form pairs with odd composites.

Table 1. The Ratio of Primes to Composites

Table 1 presents ratios, with 'b' (highlighted in yellow) as the denominator when considering even number 'n,' 'c' (highlighted in blue) as the denominator when considering the number of odd composites, and 'd' (highlighted in red) representing these ratios. If the number of odd composite pairs exceeds 'd,' it implies the existence of at least one pair of odd prime numbers.

This allows us to discuss uncharted areas, such as empirical and limit-based investigations, by substituting them into the upper and lower limits of odd composite pairs.

Empirical Measurement of the Ratio of Odd Composites and Odd Composite Pairs:

The count of odd pairs (excluding 1) up to the even number n is determined as "f = n/4 - 1". The number of pairs between odd composites and odd primes can be calculated from empirical data as "i = b - 2g - 1". The count of odd prime pairs is related to "h = f - g - i".

Table 2. Empirical Measurement of the Ratio of Odd Composites and Odd Composite Pairs

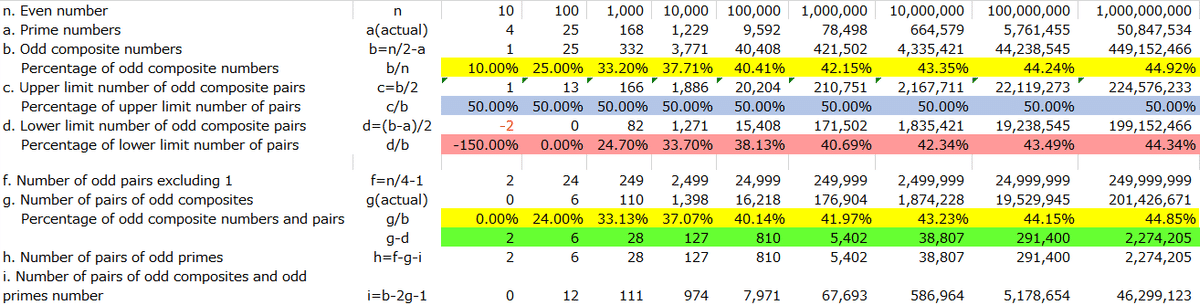
In Table 2, it is evident that the ratios of b/n and g/b are remarkably close and proportional. Moreover, their positions fall within the intermediate range where c>g>d, as highlighted. The difference represented by g-d (highlighted in green) corresponds to the number of prime pairs for even n. This indicates that pairs of odd composites systematically emerge from odd composites at regular intervals.

Ratio of Primes and Composites Based on the Prime Number Theorem:

Next, we calculate the number of odd composite pairs "g = b²/n" under the assumption that the ratio of primes and odd composites b/n and the ratio of odd composite pairs to odd composites g/b are equal, based on the Prime Number Theorem.

Table 3. Ratio of Primes and Composites Based on the Prime Number Theorem

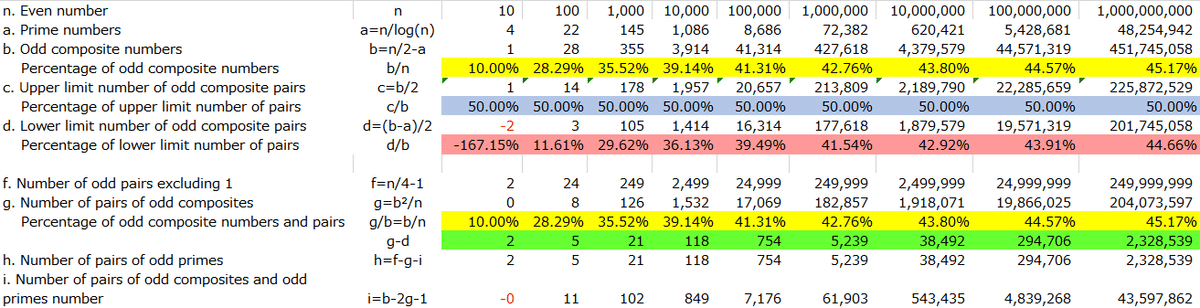
Table 3 demonstrates the ratios obtained based on the Prime Number Theorem. "b/n" represents the ratio of composites to the total even numbers up to n. "g/b" indicates the ratio of odd composite pairs (g) to the total number of odd composites (b). These ratios confirm that, as n increases, the number of primes adheres more closely to the Prime Number Theorem, and the position of g lies between the values of c and d.

Figure 1. The Mechanism: How Even n Growth Boosts Prime Pairs

The underlying principle here is that as even n becomes larger, it results in an increase in the number of prime pairs. This is based on the premise that when n is a large even number, it can be expressed as the sum of two odd prime numbers. As n grows, there are more opportunities to find such pairs of prime numbers that add up to n. Consequently, as n increases in magnitude, the number of prime pairs that can be identified also increases.

Conclusion:

From the results obtained, it is evident that there exists at least one pair of odd primes based on empirical data and theory. While proving the positional relationship of pairs for even n is challenging in the case of primes, it is achievable for composite number pairs within even n. This demonstrates that the ratio of primes and composites assures the existence of at least one prime pair greater than or equal to 1, even in uncharted territory.

References:

[1] Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Volume 1), St.-Pétersbourg 1843, pp. 125–129
[2] Oliveira e Silva, Tomás. "Goldbach conjecture verification." sweet.ua.pt.

Acknowledgments:

Acknowledgments: I would like to express my gratitude to those who engaged in discussions on web forums and to ChatGPT for their contributions to this solitary research.

---

Request for a Letter of Recommendation for Submission to a Peer-Reviewed Journal: To support the submission of this significant contribution, I kindly request a letter of recommendation from a qualified mathematician with expertise in the relevant field. The letter should be signed and written on official letterhead, confirming their understanding of the arguments presented in this paper and attesting to its correctness.

Please note that physical letters, not electronic, are required for submission and should be sent by regular mail. Thank you.

---