
LC周波数フィルタの設計パラメータ
今回も完全自分用備忘録用記事です。
高周波回路用の周波数フィルタを設計するためのメモにつなげるためにLCフィルタを中心にまとめました。そのためRCフィルタは扱わず、またOP AMPなどを使わないパッシブフィルタのみを考えます。
1回ですべてをまとめることは難しいので今回はフィルタの設計をする際の指針をまずはまとめています。
1.フィルタの種類
まずはどのような周波数の信号を通したいかを決めてあげる必要があります。主に4種類のフィルタがあり、場面に応じて使い分けます。
ローパスフィルタ:ある周波数よりも低い信号だけを通すもの
ハイパスフィルタ:ある周波数よりも高い信号だけを通すもの
バンドパスフィルタ:ある周波数の範囲にある信号だけを通すもの
バンドエリミネーションフィルタ:ある周波数の範囲にあるものだけを通さないもの
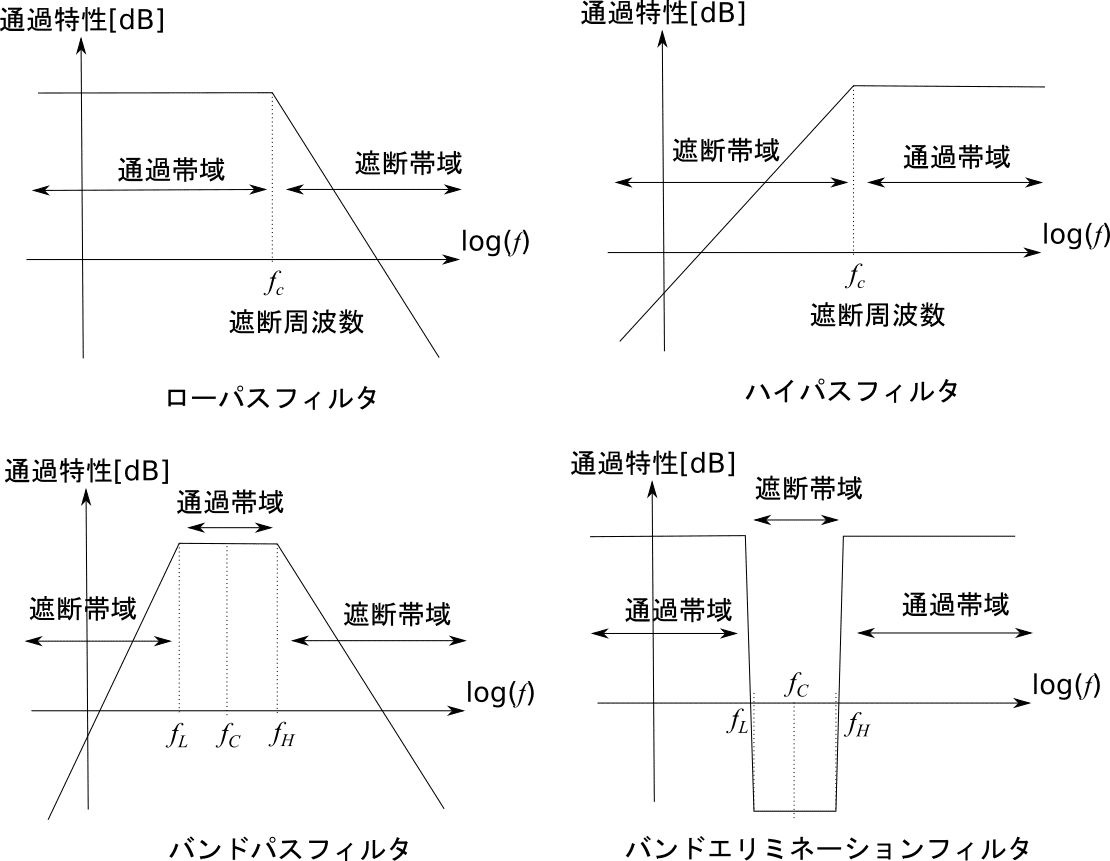
ローパスフィルタは一般に高域のノイズを落とすために、ハイパスフィルタはDCを落としたり低域の制御用信号をカットするために使用されます。
バンドパスフィルタは不要な帯域のノイズを落とすために使われますが、どちらかというと信号の周波数が高いRF部やIF部で使われることが多いです。バンドエリミネーションフィルタは電源周波数や導波管のカットオフ周波数などの特定のノイズを落とすために使用されます。
2.フィルタのトポロジー
LC回路には回路トポロジーとしてT型と呼ばれるものとπ型と呼ばれるものの2種類があります。この素子ブロックの中にLやCといった受動素子や、LC直列/並列共振回路などを埋め込んでいくことでフィルタを作ることになります。T型とπ型のトポロジーは通過帯域では数学的には等価で、どちらを選んでも構いません。遮断周波数では0Ω側にいくか∞Ω側になるか変わるので、どちらにするか気にすることも一応あるでしょう。

3.フィルタの次数
LCフィルタでは使用する素子ブロックの数に対応する「次数」と呼ばれるものがあります。電気特性を考えるとフィルタの次数は遮断時の傾きに関係します。
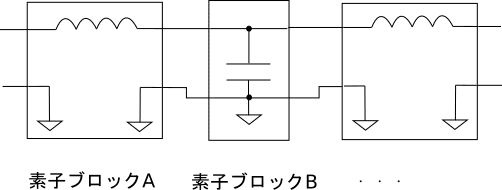
LCフィルタの場合、直列素子とシャント素子が交互に現れますが、この一つの直列素子又はシャント素子のブロックを素子ブロックと呼びます。例えば下の図では次数3のT型ローパスフィルタのトポロジーとなっています。
バンドパスフィルタやバンドエリミネーションフィルタの場合、一つの素子ブロックの中にLC並列共振回路やLC直列共振回路を入れることになります。
素子数で決まる次数ですがこの特性を考えるとn次のローパスフィルタの傾きはn×20dB/dec.またはn×6dB/oct.(周波数が10倍になるとn×20dBだけ通過信号が落ちる、または、周波数が2倍になるとn×6dBだけ通過信号が落ちる。これら表現が違いますが意味は同じです。)となります。これはハイパスフィルタやバンドパスフィルタなどでも同じで、次数が大きいほど急峻な特性となります。

次数が大きくなると遮断帯域の信号を大きく落とすことができますが、素子数が増えるので物理的なサイズが増えたり素子のばらつきの影響が大きくなったり素子が持っている抵抗による通過損失が大きくなったりします。そのため必要最低限の次数を使うことが重要です。
4.フィルタの入出力インピーダンス
フィルタの入出力インピーダンスも設計パラメータになります。通常50Ω入出力としますが、当然100Ω入出力などのほかのインピーダンスでも構いません。ただし、0Ω出力∞Ω入力は高周波系では現実的ではないので今回は扱いません。
50Ω入出力とした場合、フィルタの次数は3以上の奇数次となります。
5.フィルタの型
フィルタにはそれぞれ特徴を持った型があります。特性としては遮断周波数での折曲がりの速さ(ロールオフ特性)と群遅延特性、通過帯域でのリップルの大きさに関係します。
A.バタワース型
癖が少ない最も自然なフィルタだと思います。なんとなく設計するのであれば、初めはこれで設計しても良いかもしれません。
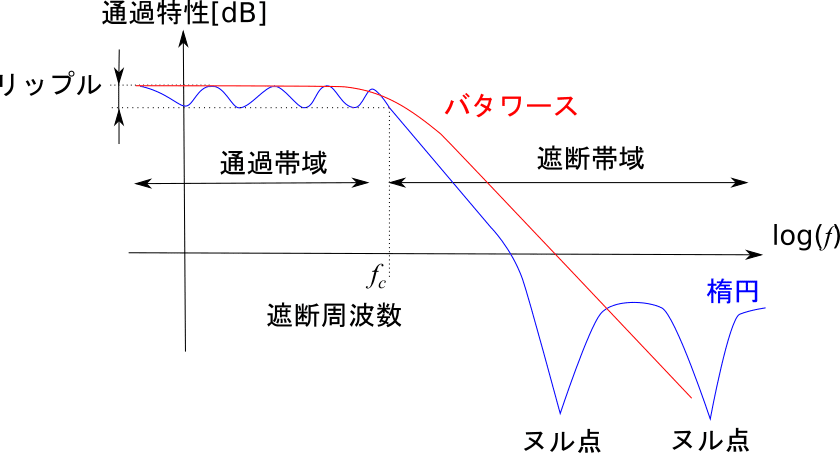
バタワース型の特徴は
・通過帯域の周波数特性が平坦
・遮断周波数の定義が通過特性が-3dBとなる周波数
B.チェビシェフ型
通過帯域でのリップルを許容する代わりに遮断時周波数での折れ曲がりが早めに発生することが特徴のフィルタです。このフィルタを設計する場合、リップルの大きさというパラメータが追加で必要です。
チェビシェフ型の特徴は
・通過帯域がリップルを持つ
・遮断周波数付近での折れ曲がりが早い
・群遅延が悪い
・遮断周波数の定義が通過特性がリップルの大きさと同じになる周波数

C.楕円型
楕円型フィルタは通過帯域でのリップルだけでなく、遮断周波数でのヌル点を持たせることで、遮断周波数での折れ曲がりをチェビシェフ型よりもさらに早く発生させることができるフィルタです。
楕円型の特徴は
・通過帯域がリップルを持つ
・遮断帯域でヌル点を持つ(遮断帯域内のヌル点間で通過特性が有限)
・遮断周波数付近での折れ曲がりがチェビシェフよりも早い
・群遅延が悪い
・遮断周波数の定義が通過特性がリップルの大きさと同じになる周波数
D.ベッセル型
正直な話、使ったことがないです。遮断周波数付近での折れ曲がりをゆっくりにする代わりに群遅延特性を極力平坦にしたものです。これは実時間での波形の歪みを小さくするためのもので、立ち上がりのリンギングなどを抑える必要があるデジタル回路などで使われるのではないかと思われます。
ベッセル型の特徴は
・通過帯域の周波数特性が平坦
・遮断周波数付近での折れ曲がりがゆっくり
・群遅延の周波数特性が平坦
・遮断周波数の定義が通過特性が-3dBとなる周波数
6.設計方法
6-A.種類の決定
まずはフィルタの種類を決定します。これはどのような信号を通過させたいか、どのようなノイズを落としたいのかという純粋な回路全体の検討からある程度は自然に決定されるかと思います。
6-B.回路トポロジーの決定
次に回路トポロジーを決定します。これは部品の入手性(通常Lの方あ入手しにくい)やサイズなどの物理的な制約と、部品の寄生素子や分岐での高周波でのふるまい(T型の方がπ型よりも分岐が少ない)といった電気的な制約で決めることになります。
6-C.次数の決定
その後、フィルタの次数を決定します。フィルタの次数は遮断周波数と落としたいノイズ周波数の近さによって決まります。次数が大きくなるほど周波数領域での通過特性の傾きが大きくなるので早く落ちていきます。
6-D.フィルタの型の決定
最後にフィルタの型を決定します。これは遮断周波数と落としたいノイズ周波数が近い時にとくに重要です。フィルタの型に応じて遮断周波数付近での折れ曲がり始めの速さ(ロールオフ特性)が変わります。ここでリップルや折れ曲がり始めの速さが制約となって目標の遮断特性・通過特性を実現できない場合は次数を再度検討しなおすことになります。
また、遮断帯域でヌル点を実現したいという理由で楕円フィルタを選択することもあります。
私は経験がありませんが、信号の波形の実時間での歪み度合い(群遅延特性)に制約がある場合にもこの選択は重要なとなります。
6-E.素子定数の決定
ここまでくればあとは簡単です、LCフィルタの定数表に従って素子を選べば自動的に望みの周波数特性のフィルタが実現できます(といってもそんなに簡単ではないのですが)。もちろん実際には素子定数で入手可能なものは限られるので、それらを使うことになります。
素子定数の決定方法などは次回に回します。
