
666←PPP←RRR
The subject is the number everyone hates (or loves)...but I have no doubt that there are countless articles on this particular number #数字 #666 .
This is a rather recreational article with very little theory except for a reference to a primality test and one remark on "Crime and Punishment"("Преступление и наказание",#罪と罰) by late professor Taku Egawa (江川卓), who passed away exactly 23 years ago today🙏
Since 16661 is a prime number, one might feel inclined to look around some ominous numbers containing 666...and the first number I come up with relative to 666 is Belphegor's prime, the palindromic prime
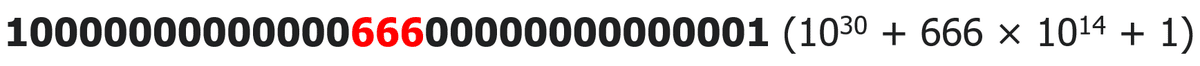
a number which reads the same both backwards and forwards and is only divisible by itself and one, explained in the following article by Atlas Obscura:
It's interesting that a symbol has been designated to this particular number with π upside down.
Some very easily verified properties of 666 are
The largest prime factor of 666 is 37, on which I wrote
The sum of the squares of the first seven prime numbers: 2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 = 666.
666 can be expressed in different ways as a sum of different primes using all ten digits (0 ~ 9), i.e.,
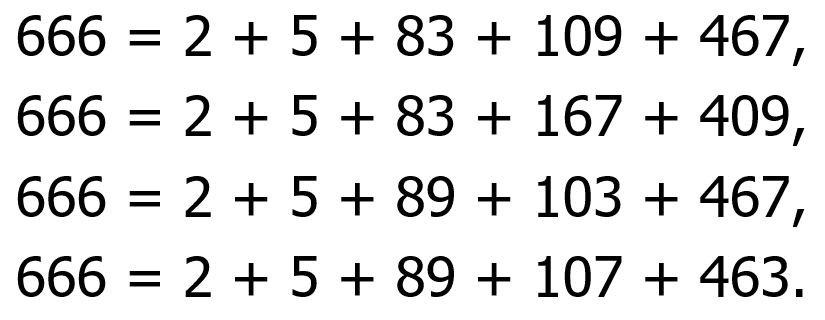
While it is very unlikely for one to calculate (x + y)³⁷ using Binomial Theorem (二項定理), 666 appears here, which is not a surprise.
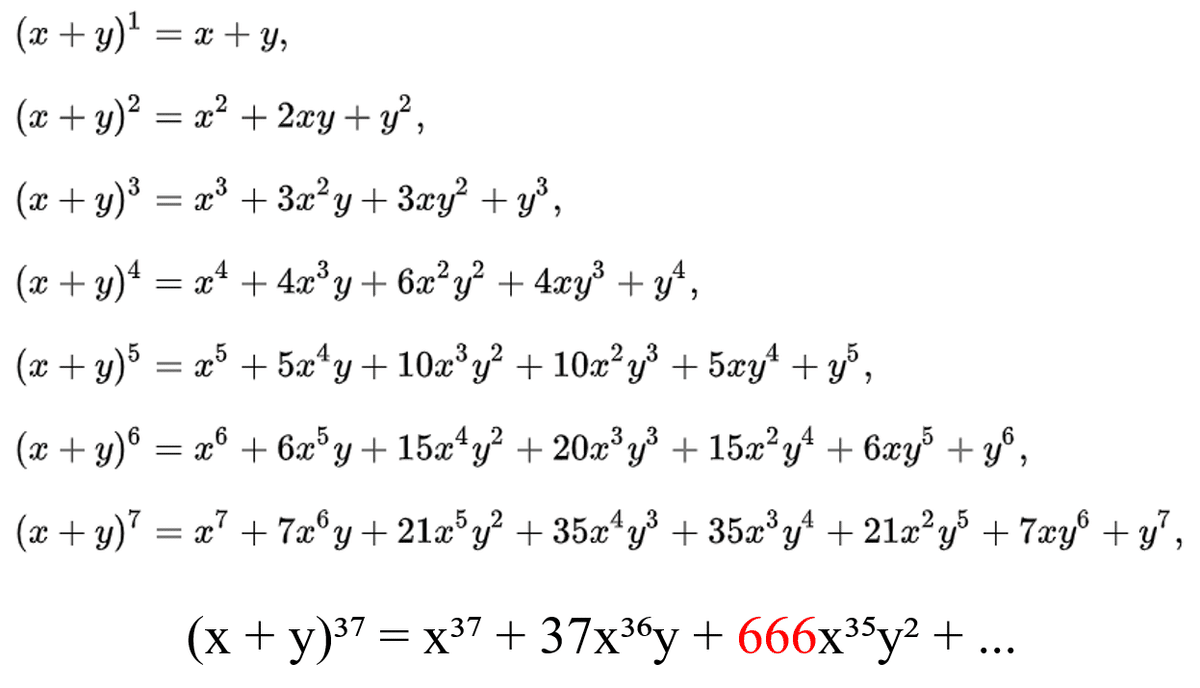
666th prime is 4973, and formation of new 7 digit numbers with 666 result in additional prime numbers:

The first beastly gap between consecutive twin prime pairs occurs between {774131, 774133} and {774797, 774799} where 774133 is the 62043rd prime and 774797 is the 62089th prime. In a sense, 774144~714496 can be called a "Twin Prime Desert". Although I'm inclined to use the word "Dune", in general "prime gap" is used instead. In other words, the following 45 prime numbers are all isolated prime numbers (which are different from lonely prime numbers):

Then we have two sets of numbers:
Apocalypse Number defined as a number having 666 digits, which is a very simple definition without any mathematics
Apocalyptic Number defined as a number of the form 2^n that contains the digits 666
A very interesting Apocalypse Number is the Fibonacci number F₃₁₈₄ :

This number is not prime since 3184 is not prime.
Apocalypse primes are given by 10^(665)+n for n=123, 1837, 6409, 7329, 8569, 8967, 9663, ... (OEIS A115983).
Year 1837 is known with 2 major earthquakes, one in Syria (Ottoman Empire) in January and the other in Chile in November:
https://en.wikipedia.org/wiki/Galilee_earthquake_of_1837
https://en.wikipedia.org/wiki/1837_Valdivia_earthquake
The latter was so devastative, and caused tsunami in Japan.
An example of Apocalyptic Numbers is 2^157. The first few such powers are 157, 192, 218, 220, ... (OEIS A007356).

These are just calculations, and I don't find any profound theory behind these numbers.
Does 666 appear in decimal expression of π ?
The answer is YES👍. The string 666 occurs at position 2,440 counting from the first digit after the decimal point:
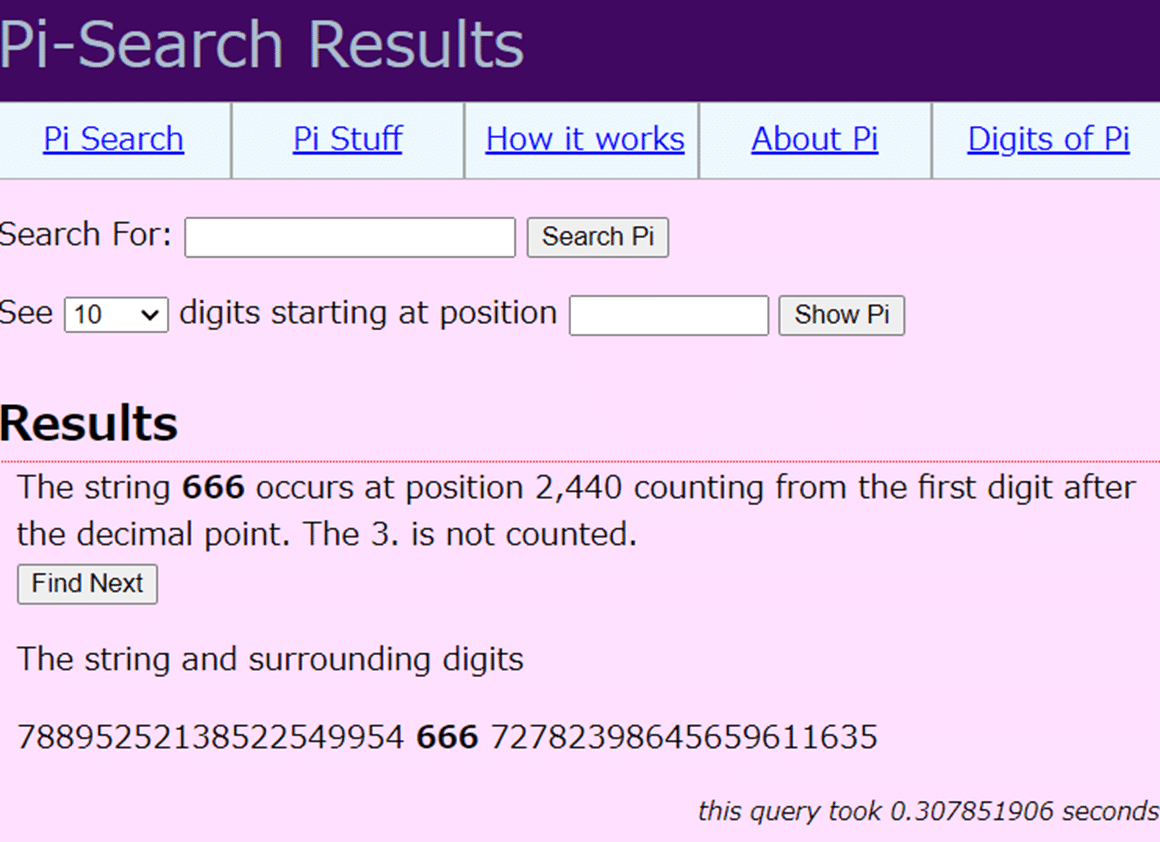
It is a bit surprising that it occurs after the Feynman point, which, according to Wolfram Mathworld, is the sequence of six 9s which begins at the 762nd decimal place of pi,
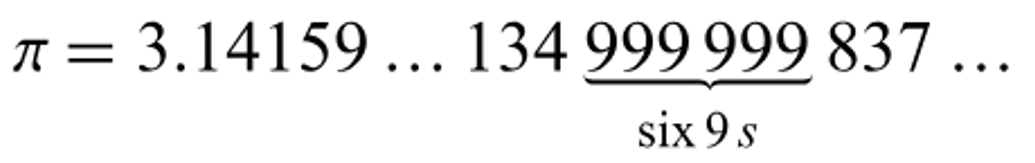
And here is from Wikipedia:

How about "Prime Days" (defined as YYYYMMDD expression being a prime number) in year 2666 ? (Not by Amazon... Rainforests will have disappeared by 2666...)
2666/01/19
2666/02/13
2666/03/03
2666/03/11
2666/03/23
2666/03/29
2666/04/11
2666/05/03
2666/05/21
2666/05/31
2666/06/03
2666/07/23
2666/08/13
2666/09/17
2666/10/01
2666/10/07
2666/11/01
2666/12/21
2666/12/27
It's meaningless to talk about year 2666 though...I'm so sure that human beings will have been annihilated either by a meteorite impact or by detonations of atomic bombs by evil states in the Eurasian continent. Perhaps I should leave this sort of thing to fortune tellers (#占い) or astrologers (#西洋占星術) 😎
Joking aside, Prime Quadruplet is a quite interesting theme for me. Skipping the first one {5,7,11,13}, these are

Except for {5, 7, 11, 13}, it has the form {30n+11, 30n+13, 30n+17, 30n+19} with n ≥ 0 an integer.
One of the intriguing facts about prime quadruplets is the following consecutive prime quadruplets with actual gap being 30, the smallest gap between prime quadruplets:
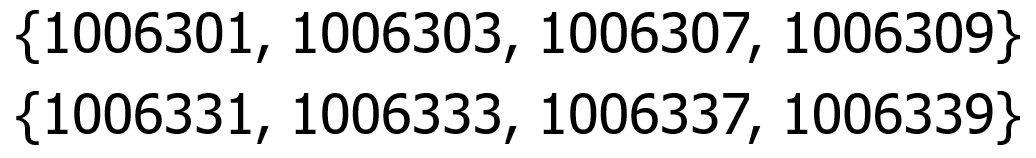
In reality, there's no prime number between 1006310 and 1006330.
Incidentally, I feel like to know any fragment of data relative to the following statement for quadruplets in Wikipedia:

As one could imagine, a "beast" exists in the set of prime quadruplets. The smallest "beast quadruplet" (666-digits) is also the smallest "beast quintuplet." (10^665 + 2969689524331 + d, where d = -4,0,2,6,8.)

I happened to learn Russian for my study of mathematics from late professor Taku Egawa (故江川卓教授, 24 January 1927 - 4 July 2001) when I was a student at an institute of technology 45+ years ago... In his book "謎解き『罪と罰』" (Crime and Punishment - a puzzle solving) published in July 1986, he writes about the name Rodion Romanovich Raskolnikov of the fictional protagonist of the novel "Crime and Punishment" by Fyodor Dostoyevsky. Its initial written in the Cyrillic script and overturned becomes 666... He also refers to the "Dictionary of Russian Personal Names", and emphasizes that the initial PPP (in Cyrillic) only appears once among 6 million Russians on average in 19th century. So Dostoyevsky did choose such a rare combination, which must have been intentional... as suggested by the evidence that Raskolnikov's first name had been Vasiliy (Russian: Василий) at the time of conception of the novel.

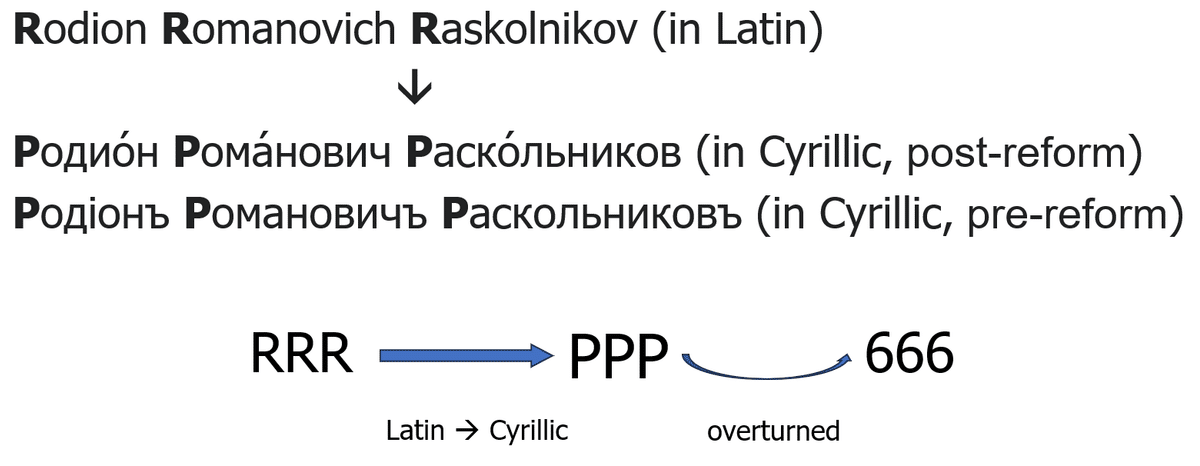

R.I.P.🙏
(NOTE. I do not know if there has been any development relative to the relationship between the initial of Raskolnikov and 666.)
In closing, the following three numbers 666 × 6(m+1) × 910 + 1 (m=0, 1, and 2) are all prime.
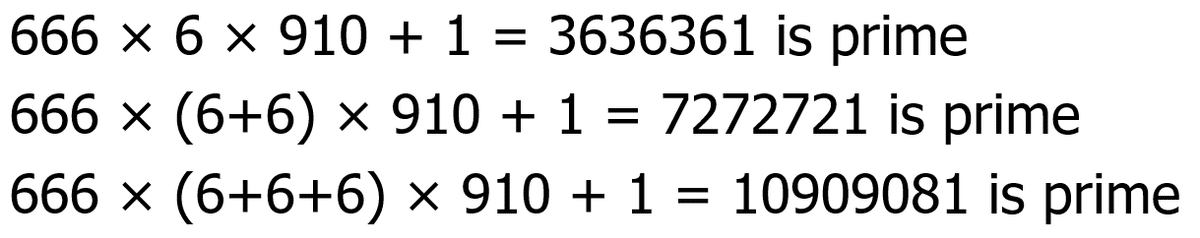
This is a very simple fact, however, using Chernick's sufficient condition, we can tell the product of the 3 numbers (288504163486697099761 = 3636361 × 7272721 × 10909081) is a Carmichael number, also called Fermat pseudoprimes or absolute Fermat pseudoprimes (絶対擬素数). A Carmichael number will pass a Fermat primality test to every base b relatively prime to the number, even though it is not actually prime.
Primality test is a very important topic in mathematics, and has nothing to do with 666. A very elementary primary test for a given number N is to see if any prime number ≤ √N divides N.
A simple but very inefficient primality test uses Wilson's theorem, which states that (p-1)!≡-1 (mod p). It's so obvious that it is impractical.
I've not studied this area, so let me stop talking about theoretical aspects of primality test. Hopefully I can cover this topic in another article after some study🧐 □
