
Prime Gaps
<Caution> Anton Pavlovich Chekhov has a novel called "A Dreary Story" 『退屈な話』(Russian: Скучная история), which is not boring at all.
I apologize in advance that this article is boring to death🙇.
The study of the prime gaps seems to be one of fertile topics in Analytic Number Theory, of which the most famous and studied one is obviously the "Twin Prime".
Whilst not being a professional mathematician, I do find the way how gaps appear very intriguing. Any even number, no matter how large, appears as the difference between two primes, which I'm inclined to call "a dune for prime numbers" (素数砂漠), but I'm afraid the word dune (or desert) is scarcely used in English in the context of big gaps between two prime numbers.
This article, continued from my post in X (Twitter), is apparently not a paper of a research, but is intended to list up some examples, none of which is pathological.
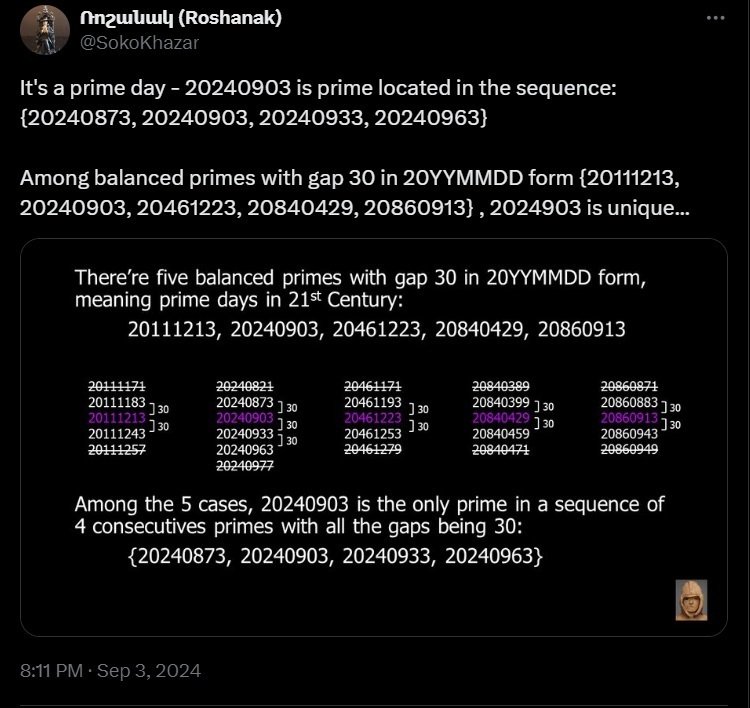
The above post in X (Twitter) shows a not rare but not common prime sequence {20240873, 20240903, 20240933, 20240963} (*), which is a sequence of 4 consecutive balanced primes with gap being 30. Here 30 is a pretty common number for a prime gap. Such a sequence exists in smaller digits such as {642427, 642457, 642487, 642517}, however, I happened to find the sequence (*) on 3rd of September 2024, expressed as 20240903 in YYYYMMDD format.
First of all, there're two ways to define a prime gap:
① Wikipedia: the difference between two successive prime numbers
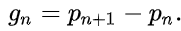
② PrimePages: the number of composites between two successive prime numbers
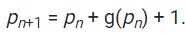
In this article I follow the former definition by Wikipedia.
Deep theories put aside, there is a table of 82 known maximal prime gaps in Wikipedia:
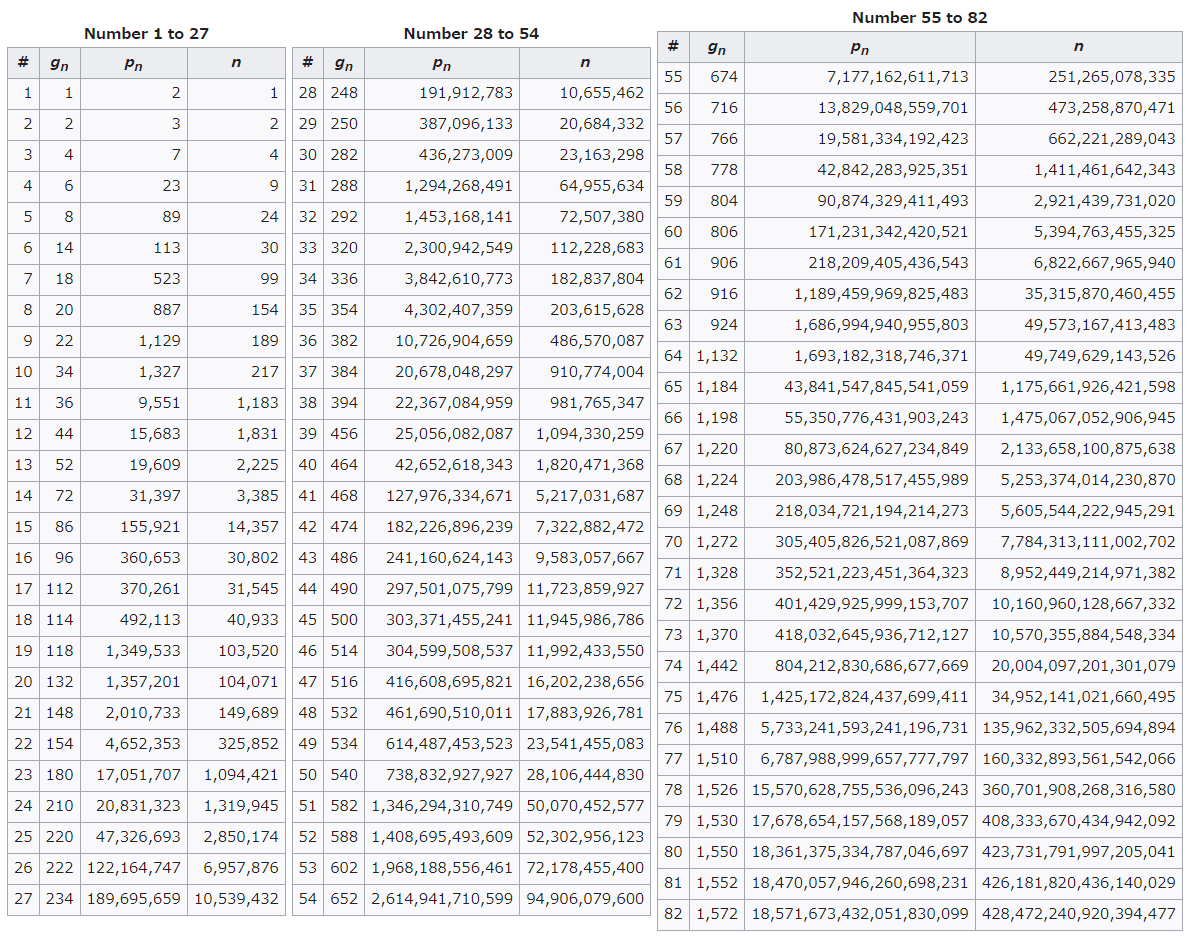
That's NOT the end of the story😉. For example, prime gap 30, 100, and 246 are not mentioned in the above table.
The first small "jump" takes place at p = 1327. Its next prime is 1361, meaning the gap 34. However, gap 30 only comes at p = 4297, the next prime of which is 4327.
Similarly, while the gap 112 appears at (370261, 370373), the gap 100 comes at (396733, 396833):

9-digit number 555142061 , which is a Chen prime because 555142061 + 2 = 7 × 79306009, gives us the smallest case of prime gap 246, while gaps 248 and 250 are attained at smaller numbers 191912783 and 387096133 respectively.
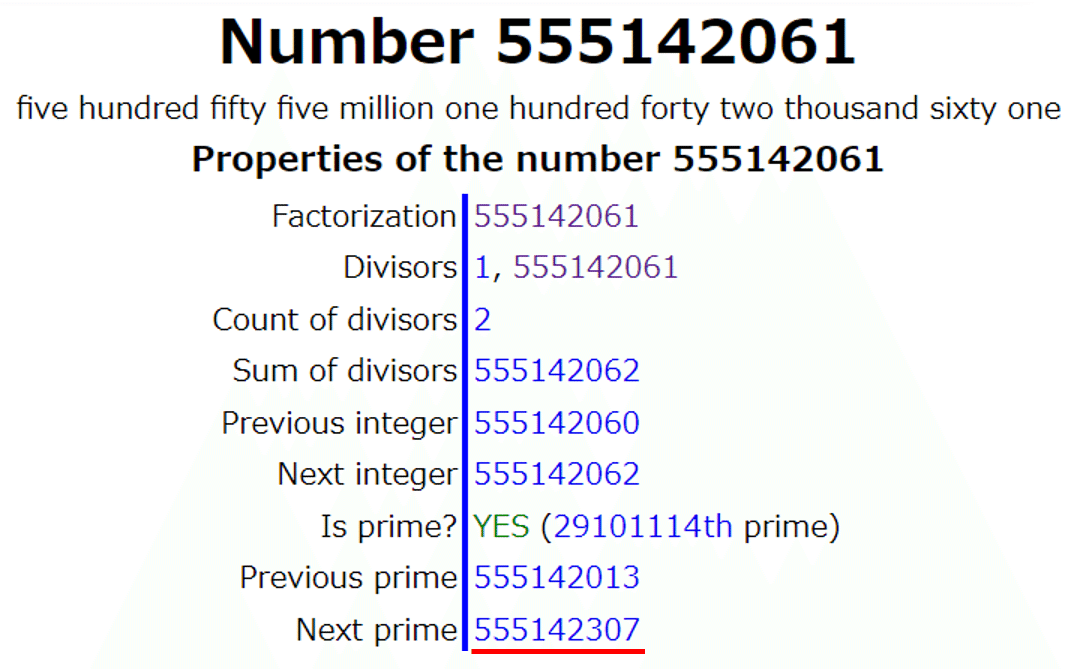
Back to 246, it is noteworthy at this juncture :
Maynard's approach was different: "Rather than improving the input to the method I changed the method itself. It became more efficient in turning one type of information into another and it meant that we needed much weaker inputs to get a result about boundary gaps between primes." With this new method he dramatically reduced the gap from 70 million to just 600. And after a flurry of collaborative work with a group of mathematicians , we now know there are infinitely many pairs of primes separated by a gap of just 246.
By Rachel Thomas, produced as part of the ICM coverage
The least prime which produces a gap (difference) of 666 is 18691113008663 (14 digits), which is a Chen prime: 18691113008663 + 2 = 5 × 3738222601733.
On the other hand, 42842283925351 (14 digits), though listed in the above table, is the least prime which produces a gap of 778 and it is far smaller than 778!+2 (which has 1914 digits).
The gap 796 = 2²× 199 is somewhat peculiar. It is only attained at (1271309838631957, 1271309838632753) (16 digits) while other gaps near 796 are attained at 14~15 digits, for example,

In order to observe prime gap 1000 exactly, one has to wait until 17-digit number 22439962446379651 with its successor being 22439962446380651.
Notably, the gap 1008 is attained at 16 digit number 5356763933625179.
Evidently, one can talk about each prime gap endlessly only being daunted. Contrary to the purpose of the above table in Wikipedia, which effectively shows "large prime gaps" which occur quite "soon", the following two examples show "less-likely-to-occur" gaps:
1382 at 11320694552053653731 (20 digits)
1492 at 316129781931380000239027 (24 digits)
In terms of less-likeliness to occur, 6466 is noteworthy. The gap only comes at 102 digit prime
834318449164207419802090262815984745059807656813863082396019907040135446976989663175939612727204389967
The next prime is
834318449164207419802090262815984745059807656813863082396019907040135446976989663175939612727204396433
The gap 10000 comes at a number with 145 digits, which I won't write.
Yet much bigger gaps do exist. In order to study prime gaps, Analytic Number Theory is required with assistance of experimental computing.
The final examples in this article are regarding prime triplets (consecutive 3 prime numbers) with the following condition:
{P₁, P₂, P₃} with P₂ − P₁ ≥ 100 and P₃ − P₂ ≥ 100 --- (*)
I found the following 4 sets less than 10⁸:
{72546143, 72546283, 72546391}
{77736271, 77736383, 77736487}
{85706693, 85706813, 85706917}
{98486461, 98486567, 98486669}
One can obviously expect a similar triplet with a different condition in (*) such as replacing 100 by 1000. One example, though not the smallest, is:
{10⁹⁹ + 1004269, 10⁹⁹ + 1005697, 10⁹⁹ + 1007193}
Please note that the following two pairs are twin prime pairs smaller and greater than the above triplets respectively:
(10⁹⁹ + 1001137, 10⁹⁹ + 1001139) & (10⁹⁹ + 1016437, 10⁹⁹ + 1016439)
However, upon changing the condition (*), if we adopt a revised condition like
{P₁, P₂, P₃} with P₂ − P₁ = 100 and P₃ − P₂ = 100 --- (**)
then, there is no such triplet. The difference 100 is not divisible by 3, therefore a triplet {P₁, P₂, P₃} includes at least one composite number. Just for an example, modifying the condition (**) with 102 instead of 100, one can find a triplet {460475467, 460475569, 460475671}.
□
Credit for the header image:
https://www.youtube.com/watch?v=BH1GMGDYndo
This is a short video featured by James Maynard, who is a leading mathematician in Analytic Number Theory and was awarded the Fields Medal in 2022, also mentioned above relative to 246.
References:
[1] https://mathworld.wolfram.com/PrimeGaps.html
[2] https://www.pzktupel.de/JensKruseAndersen/gapmainpage.php
この記事が気に入ったらサポートをしてみませんか?
