
5537, NOT 65537
Earlier this week, the number 5537 jumped out at me first thing in the morning. Since this is a four-digit integer, it's irrelevant to the discussion of the number of seats in the House of Representatives in Sunday's national elections.
Mathematically, 65537 = 2¹⁶ + 1, a Fermat prime, is far better known than 5537 thanks to a constructible 65537-gon. However, it is highly unlikely that what I had in front of me was in fact 65537 but somehow I had missed the leading 6.
One might be inclined to look into the following spiritual message:

Skipping the above readable yet incomprehensible message, 5537 = 7² × 113, so it is neither a prime nor a semi-prime. Coincidentally 637 = 7² × 13, but this is not a surprise, and does not appear to lead to anything.
113 is an interesting integer. Indeed Prime Curios for 113 contains more than 55 entries, some of which are just rubbish though.
That said, let me refer to the following facts relative to 113, which could be gibberish.
① Nihohium, first reported in 2003 and finally recognized by the IUPAC/IUPAP Joint Working Party in 2015, has atomic number 113:
"Nihonium is a synthetic chemical element; it has the symbol Nh and atomic number 113. It is extremely radioactive: its most stable known isotope, nihonium-286, has a half-life of about 10 seconds. In the periodic table, nihonium is a transactinide element in the p-block. It is a member of period 7 and group 13."

② The function defined on natural numbers as π(n)log(n)/n has its maximum value at n = 113 where π(n) is the prime counting function and log(n) stands for natural logarithm function (often denoted "ln"). This is related to the fact that the prime gap jumps to 14 at prime number 113. Similar maximal values are attained, for example, at 1327, 31397, 370261... which can be found at "The 83 known maximal prime gaps" described in Prime Gap.
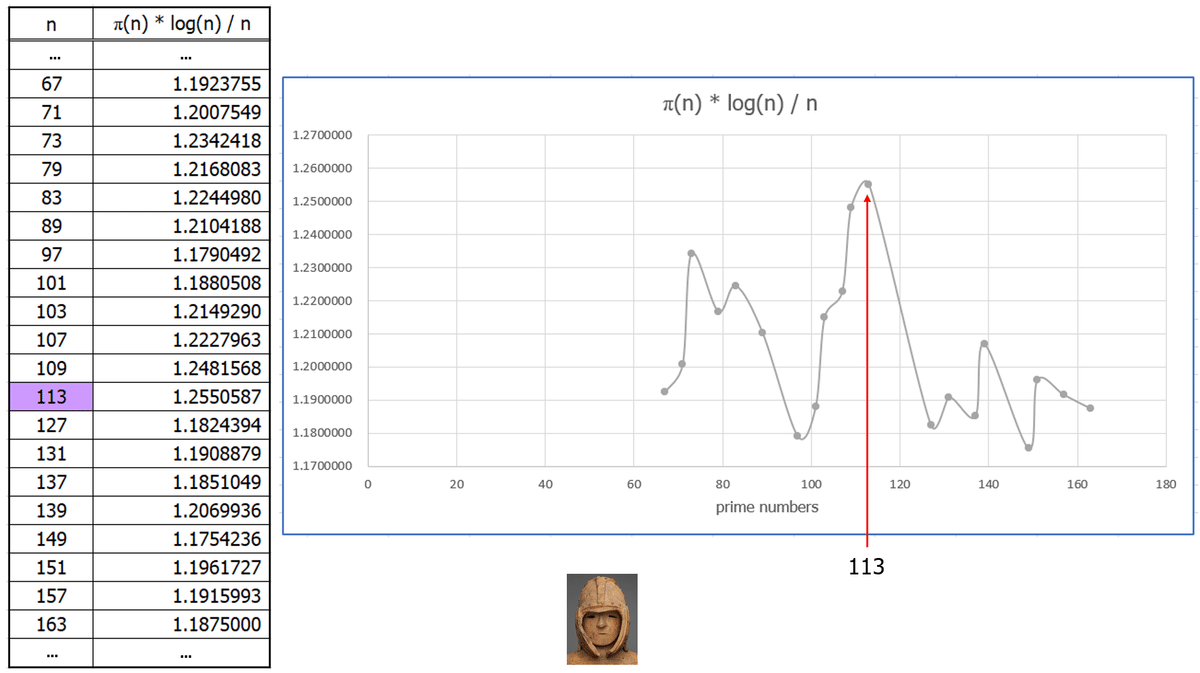
This function π(x)ln(x)/x converges to 1 when x → ∞, which is an assertion of the classical Prime Number Theorem.
③ 355/113 = 3.1415929203539823008849557522124... is the second famous fractional approximation of π.
④ 113 is 11th Sophie-Germain prime since 113 × 2 + 1 = 227 is prime. Also it's 24th Chen prime since 113 + 2 = 5 × 23.
⑤ According to Cyclotomic field (Wikipedia), 113 is a prime factor of the class number of Q(ζ₈₉), which is 13379363737 (11 digits ) = 113 × 118401449. On the other hand, the class number of Q(ζ₁₁₃) is 1612072001362952 (16 digits) = 2³ × 17 × 11853470598257.
Back to 5537
Its last two digits are 37. A simple calculation shows there're 29 primes of 4 decimal digits with the last two digits being 37, while there're 1061 primes of 4 decimal digits, which means that around 2.7% of 4 digit primes have 37 in their last two digits.
1237, 1637, 2137, 2237, 2437, 2837, 3037, 3137, 3637, 4337, 4637, 4937, 5237, 5437, 5737, 6037, 6337, 6637, 6737, 7237, 7537, 7937, 8237, 8537, 8737, 8837, 9137, 9337, 9437
This leads to a more general question, and as a matter of fact there are some professional researches relative to distribution of prime numbers from the perspective of the last digit (in decimal expressions).
Another question might arise whether there exists a prime number of the form 55…5537. The answer is NO. Any integer of that form is divisible by 3, 7, 13 or 37, owing to 555555 = 3 × 5 × 7 × 11 × 13 × 37.
Incidentally, by switching the last two digits, 5573 is a prime and there're 27 primes of 4 decimal digits with the last two digits being 73. Interestingly, the following integers are prime:
55555573
55555555555573
5555555555555573
55555555555555555555555555555555555555555573
...
Here is a comparison of factorization of integers of the forms 55…5537 and 66…6637:

A bit more on 65537…
The following intriguing YouTube video "An Odd Property of the Sierpiński Triangle" by Numberphile shows the relationship between binary representation of constructible polygons (or the modulo-2 Pascal's triangle) and the Sierpiński Triangle breaks at 2³² + 1, which is called the 5th Fermat number factorized as 2³² + 1 = 4294967297 = 641 × 6700417, a well-known factorization by Leonhard Euler in 1732.
As of today, 65537 is known to be the largest Fermat prime, which shows a stark difference from the Mersenne prime. Let's recall that a new Mersenne prime was just announced on 21st October 2024 by GIMPS:
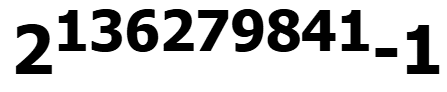
At 41,024,320 digits, it eclipses by more than 16 million digits the previous largest known prime number found by GIMPS nearly 6 years ago.
Luke Durant, GIMPS most prolific contributor using free GIMPS software, proved the number prime on October 12. After notifying the GIMPS server, GIMPS began a rigorous process of independently confirming the prime number on several different hardware platforms using several different programs. This process concluded on October 19th.
The following YouTube video explains that this particular number was found in a different manner from the way how the previous one was found in December 2018:
For those who have not heard of the Sierpiński Triangle, the following site is helpful in addition to Wikipedia.
https://virtualmathmuseum.org/Fractal/Sierpinski_triangle/Sierpinski_triangle.html


https://www.eejournal.com/fresh_bytes/more-than-you-ever-wanted-to-know-about-the-sierpinski-triangle/
Header image credit : First Union Rail (FURX) #5537 , CSXT Manchester Subdivision, Union City, Georgia, taken by David Stewart on 21st August 2014 (via RailPictures.NET).
