
蜂の巣の不思議な幾何学(2):五角形と七角形の法則性
まさかの記事の続きを書く日がくるとは!
以前次の記事を書きました。
簡単に説明すると、蜂の作る部屋は通常六角形なのに、少し大きな女王蜂の幼虫の部屋が存在すると、五角形と七角形の変形部屋が作られる、というものです。
具体的には次の図のような構造になっています。

上が小さい部屋で、下が大きい部屋。これが1/4対1/3の対応になっているときに、蜂さんがクッションのような部屋として五角形(赤)部屋と七角形(緑)部屋を作るという、今見ても不思議不思議な現象です。なんでこうなるの?
数学的ルールがやっぱりあった
そんな不思議な現象について、まったく別のことから、法則性(アルゴリズム)にたどり着きました。いきなり結果を書いてしまいますと、それは、
ボロノイ図
です。
Wikipediaから引用すると、次ようなものです。
ある距離空間上の任意の位置に配置された複数個の母点(英: site、サイト)に対して、同一距離空間上の他の点がどの母点に近いかによって領域分けされた図のことである。
数学者でもなんでもない私が、なぜボロノイ図にたどり着いたかというと、Illustratorで作図しているときに、たまたま聞いたことないワードを知って興味をもっただけのこと。まさに偶然ですね。
ボロノイ図がどんなものかというと次になります。

まず、ランダムに母点(赤い点)を配置しておき、それに対して境界面を描いたものがボロノイ図です。自然界でいえば、泡とか細胞といったものの組成ルールということになるかと思います。
ボロノイ図で六角形が描けた!
しばらくランダムな母点からボロノイ図を作って遊んでいたのですが、ふと気になることを思いつきました。それが、
これって、点が規則的に並んでいたらどうなるの?
早速やってみました。
まず、母点を縦横にそろえて並べてみるとこうなります。四角の部屋ができましたね。

次に、母点を交互に並べるとこうなります。なんと、六角形の部屋(ハニカム構造)ができました。
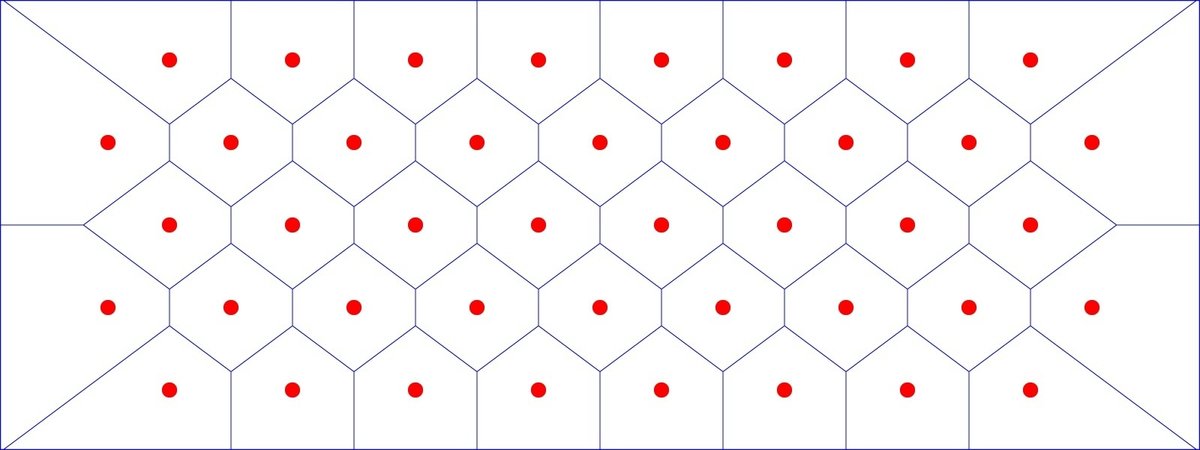
ボロノイ図というのは、母点の相互関係で文様が変わるのですね。
蜂の巣で試したらどうなるんだ?
ここで閃きました。
例の蜂の巣の配置だったらどうなるの?
次は、上が私が実際の蜂の巣から手作業で作図したもの。下が、上図の位置関係を母点として描いたボロノイ図となります。


なんということでしょう。ちゃんと、五角形と七角形の部屋ができています。つまり、蜂はボロノイ図の描画アルゴリズムで部屋を作っていたということでしょうか? ボロノイ図自体が、安定的な収束形態だとするならば、なるべくしてなったともいえるのですが、それも含めてやっぱり蜂さんてば、天才すぎますね。
蜂はどう全体配置を考えているのか?
作っているのは小さい蜂です。上から俯瞰して全体の部屋の配置を決めている可能性もありますが、行き当たりばったりで作っていたら偶然こうなった可能性もあるでしょう。そんな感じで本当に成立するものなんでしょうか? 自分が蜂になったつもりで考えると、まだまだ疑問は尽きません。
このあたりの解明には、蜂がどのような工程で部屋を作っているのか、その成り行きを観察するしかないので、専門家に丸投げさせていただきます(笑)。
一方で、ボロノイ図というルールを使うことで、蜂の通常サイズの幼虫と女王蜂サイズの幼虫が1/4対1/3のときだけでなく、他の対比についてもシミュレートすることができますね。
次は、私が作図した1/5対1/3の、たぶん自然界にはない鉢の巣です。これについてもボロノイ図を生成してみたところ、ちゃんと五角形と七角形の部屋ができました。


法則性がわかってくると、いろいろなパターンを試すことができるので、実に楽しいですね。
