
🌳樹状再帰(Tree Recursion)は影分身 樹状累積法はカタモーフィズム

いきなり、樹状といわれてもよくわからない。引数を変えて結果を見ていく






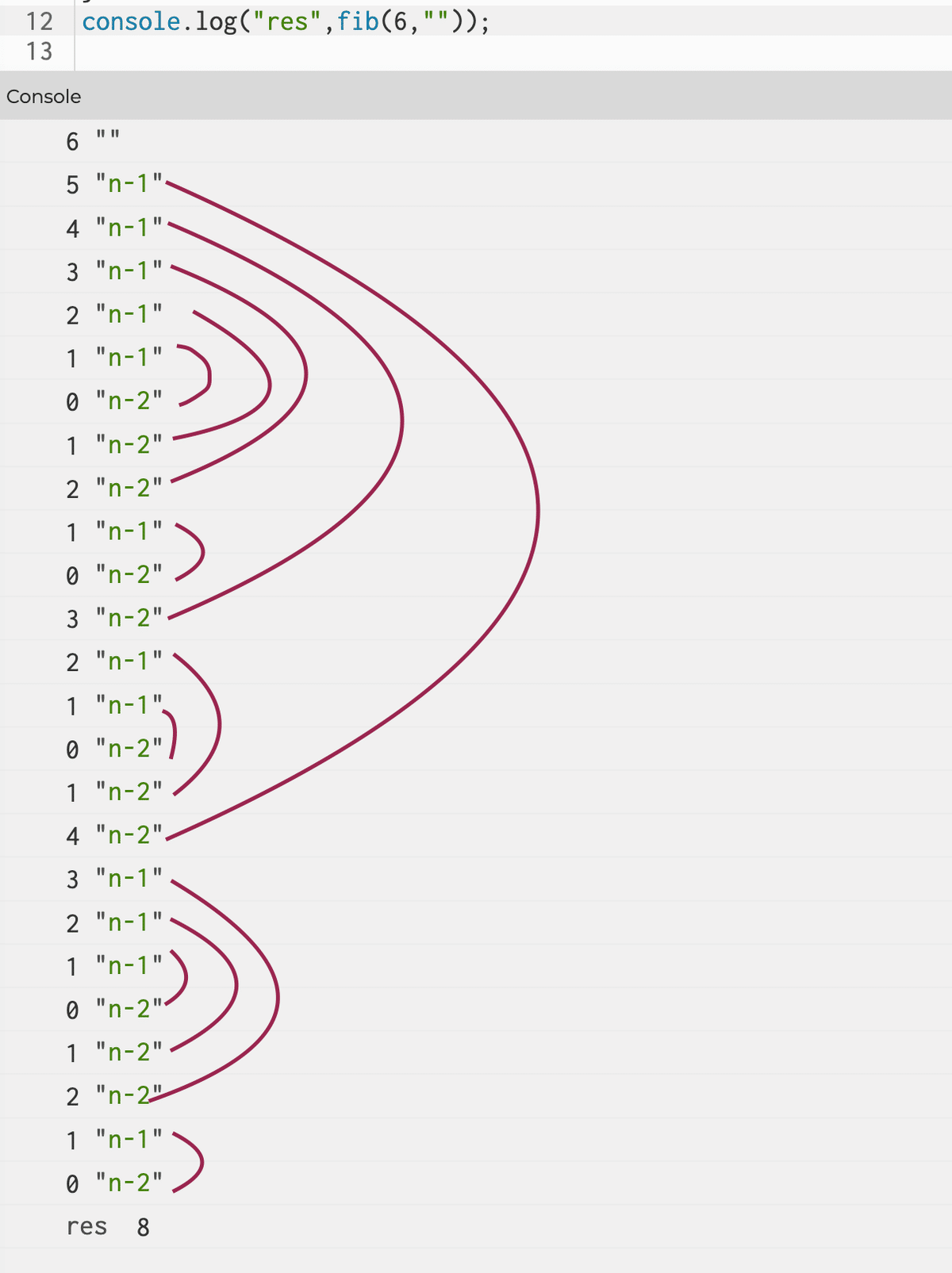
この関数は、木の再帰の原型として有益ですが、冗長な計算を多く行うため、フィボナッチ数を計算する方法としては最悪です。
といって、説明は再帰ではない例に続いていく

樹状累積法 Tree accumulation
コンピュータサイエンスにおいて、木のノードに置かれたデータを木の構造に従って蓄積すること[1]。 形式的には、この操作はカタモーフィズム(catamorphism)である。
上方への蓄積とは、各ノードにすべての子孫の情報を蓄積することである。下方向への蓄積とは、各ノードにすべての祖先の情報を蓄積することである。
応用例として、国政選挙結果の計算がある。ルートノードを国全体とし、各レベルを州・県、郡・小区、市・町、投票区などの細かい地理的な領域を葉とするツリーを構築する。投票区の得票を積み重ねることで、より大きな地域ごとの得票を計算することができる。
。
樹状再帰 (Tree Recursion)
特徴: 関数が複数回自身を再帰的に呼び出す。
利点: 簡潔に問題を表現できる場合がある。
欠点: 計算の重複が多く、効率が悪いことが多い。
末尾再起 (Tail Recursion)
特徴: 関数の最後の操作として自身を再帰的に呼び出す。
利点:
一部のプログラム言語やコンパイラで最適化されることがあり、深い再帰呼び出しでもスタックオーバーフローのリスクが低減する。
スタック使用量が一定である。
欠点: 末尾再帰を適用できる形にアルゴリズムをリファクタリングするのが難しい場合がある。
通常の再帰 (Simple Recursion)
特徴: 関数が自身を再帰的に呼び出す。この呼び出し後に追加の計算や操作が行われることが多い。
利点: 問題の自然な表現形式として適している場合が多い。
欠点: 再帰の深さが深くなるとスタックオーバーフローのリスクが増える。
「Binary Indexed Tree (BIT)」および「Fenwick Tree」は、実は同じデータ構造を指しています。Fenwick Treeとしても知られるこのデータ構造は、Peter M. Fenwickが1994年に発表した論文において紹介されました。
以下、BIT (Binary Indexed Tree) についての簡単な解説です。
Binary Indexed Tree (BIT) の特徴:
効率的な累積和の計算: BITは、配列の特定の要素の値を更新しつつ、任意の範囲にわたる累積和を効率的に計算するためのデータ構造です。
二分木の性質: 内部的には、ビット操作を活用した二分木の性質を持っています。
空間効率: 基本的に元の配列と同じ大きさの空間を使用します。
主な操作:
更新 (Update): 特定の要素の値を更新する。これは、配列の特定の位置に値を追加する形で行われます。計算量はO(log n)。
累積和の計算 (Prefix Sum): 配列の先頭から指定された位置までの累積和を計算する。計算量はO(log n)。
[オプション] 範囲の和 (Range Sum): 2つの累積和の計算によって、指定された範囲の和を計算することができます。
使用例:
BITは、累積和の問題や、値の更新が頻繁に行われるような状況での範囲にわたる和の計算などに適しています。例として、数列における逆数の数を計算する問題や、動的な配列の要素の合計値を取得する問題などが考えられます。
樹上累積法(tree accumulation)は、ある種のデータ構造である「木」に対して、その構造を保ったままの変換や情報の収集を行う手法の一つです。この概念は、特に関数型プログラミングの文脈でよく議論されます。
カタモーフィズム(catamorphism)は、あるデータ構造を「畳み込む」ための一般的なパターンです。具体的には、データ構造を再帰的に分解しながら、それに基づいて新しい値やデータ構造を構築する操作を指します。
樹上累積法は、木のデータ構造に対するカタモーフィズムの一例と見なすことができます。木の各ノードに対して再帰的に操作を行い、それを基に新しい値やデータ構造を構築することが樹上累積法の主な特徴となります。
いいなと思ったら応援しよう!

