見出し画像

🚀七行テトリス

あたり帳簿 
<body id=D onKeyDown=KEY=event.keyCode-38><script>Z=X=[B=ROW=12];function Y(){for(C
=[q=c=i=4];f=i--*KEY;c-=!Z[h+(KEY+6?p+KEY:C[i]=p*ROW-(p/9|0)*145)])p=B[i];for(c?0:KEY+6?h
+=KEY:t?B=C:0;i=KEY=q--;f+=Z[ROW+p])k=X[p=h+B[q]]=1;if(e=!e)if(h+=ROW,f|B)for(Z=X,X=[l=
228],B=[[-7,-20,6,h=17,-9,3,3][t=++t%7]-4,0,1,t-6?-ROW:2];l--;)for(l%ROW?l-=l%ROW*!Z[
l]:(SCORE+=k++,c=l+=ROW);--c>ROW;)Z[c]=Z[c-ROW];for(S="";i<240;S+=X[i]|(X[i]=Z[i]|=++i%ROW<
2|i>228)?i%ROW?"■":"■<br>":"＿");D.innerHTML=S+SCORE;Z[5]||setTimeout(Y,99-SCORE)}Y(h=e
=KEY=t=SCORE=0)</script>

まず動かす

p5.jsが楽なのでそのまま貼り付けて動かす

こんな感じ

数を数える


まず横幅が１２個の■であるのがわかる。

縦は２０行あるので、画面は横１２文字ｘ縦２０文字＝２４０個の四角文字で構成されているのがわかる。

基本的な知識をうる

キーコードについて

０ｘ２６は１６進数だが、カッコ内の３８が我々が日常生活でつかっている十進数だ、３８が上キーで、その前後に左右（３７，３９）が配置されているのに注目する。これも後で読むソースに関連が出てくるのがあるある。
スペースが３２なのにも注目


これらを踏まえて、ソースを眺めてなんとなく言語化する

さっき言った１２とか３８とか３８－６＝３２とか２４０とかソース中にでてくる。ここに関係を見出すのが人の情でありコンピューターの言語だ。

（ほぼ）定数（最後まで値が変わらないもの）になっているものの書き換え、AとかKとか

Aは横幅１行分ということでROW、KはキーなのでKEYとする、KEY+6はスペースとかんがえる。KEYがかりに３２だとすると、キーダウン時に３８マイナスしているので、ー６がはいっているはずなので、６を足すと０になる。KEY＋６の隣は必ず？が来るので、このあたりでスペース押してるか（回転するか）みたいなことをしていると予想する。ちなみに左右キーでは３８引くとー１、＋１が入ってるので、単純にKEYを足している箇所があるなら左右移動している。（はず）。

描画部分にあたりをつける

いろいろ難しいことはあるが、後半でブロックとスコアの描画を毎回行っているということにする。Sに描画するすべてを入れ込んでいて、XとZでいろいろやっているはずだが、まだややこしいので、とにかく描画している雰囲気だけつかむ。Pは影響も少ないので（pointのP）SCOREと書き換えてみる。

FORの構文を見る。

短いコードを志すひとはFORの構文の中でいろいろやっているので、FORの構文をMDNでいいので今一度叩き込んでおく。

https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference/Statements/for

for (initialization; condition; afterthought)
  statement

for文の解説を今読むと、初めてforを習った時からすると、驚くほど単純かつ自由度があるのに気づく。

最初に評価される式のブロック（initialization）があって、終了を判定するために毎回呼び出される式のブロックがあって（condition）最後に次の評価がされる前に評価される式のブロック（afterthought）がある。このコードには５つのfor文があってそれぞれ４ブロックに分けられるので、for文も尊重して以下のように整理する

繰り返し出てくる表現に理由がある

ここまで無駄をそぎ落としたコード表現なので、同じような書き方が何度も出てくるという事は、省略のしようがないということになる。気になるのはKEY+6が２回出てくるので、これはスペースキーを押したときに二種類処理があるということと、ROW（１２）は何度も何度も出てくる。比較したり足したり、引いたり、MODしたり掛け算したりいろいろするが、ROWがらみで行われていることについて明確にイメージを持つためにはテトロミノについてある程度わかっていたほうがいいようだ。


テトロミノは鏡像も入れると七種類ある


数だけ気にするとここのBが七種類あって、ｔをインクリするごとにブロックを切り替えているように思う。配列の長さも４つなので、うまいことやるとこれで七種類表現できるんだろう。

すべてのｈ が１７になるということ

Bが毎回姿を変えるブロックだとしてもｈはいつも１７になるし、Ｂの１番目と２番目はそれぞれ０と１、３番目はー１２か２だ。１７はおそらく１２＋５で、ブロックの登場の開始位置のことを言っていると予想する。つまり、毎回ブロックの起点になっているのはｈ＝１７でこれはｘ、ｙにするとｘが５でｙが１ということになる。

ここ（１７＝１２＋５（＝12/2-1））がブロックの開始位置

そうするとBの計算を何らかのオフセットだと考えると、ｈ＝１７をゼロとして、きれいにテトロミノが作れそうなのがわかる。

１７はオフセットと考えて０にする。そこから引いたり足したりする計算でテトロミノが作れる

最後に残る謎、回転

盤上のイメージを持ったうえで処理を追うと、それほど複雑な印象もなくなってくるが、最後まで異質なのは１４５という謎の数字で、これを解説してくれる人はどこにもいなかった。回転をしているというのは前後からわかるのだが、１４５というのがどういう根拠なのかよくわからない。

7: 回転先の座標を回転行列を用いて計算
回転行列は (x',y') = (cos sin, -sin cos)(x,y) というやつです。
ブロックの座標が p=x+y*12 で表されるため、x=p%12, y=Math.round(p/12) を求める
ただしビットORを用いることで実数→整数変換可能なので、
Math.floor(p/12) と p/12|0 が等価になる
ここでは、Math.round でありフィールドの大きさが小さいため p/9|0 が y に等価

https://web.archive.org/web/20190103104733/http://www.geocities.jp/nanagyou/kaisetsu.html



ビットORを用いることで実数→整数変換可能:
JavaScriptにおいて、数値nに対してn|0というビット操作を適用すると、nの小数部分が切り捨てられ、整数に変換されます。これは、浮動小数点数を整数に変換する際の高速な方法として知られています。
Math.floor(p/12) と p/12|0 が等価になる:
ここで言いたいことは、Math.floor(p/12)（p/12の結果を小数点以下で切り捨てる）とp/12|0（p/12の結果をビットORを使って整数に変換する）が同じ結果になるということです。具体的には、両方ともp/12の小数点以下を切り捨てる効果があります。
ここでは、Math.round でありフィールドの大きさが小さいため p/9|0 が y に等価:
これは少し情報が足りないため完全な解釈は難しいですが、一般的にはp/9|0の結果がyと等しいということを示しています。

この式C[i]=p*A-(p/9|0)*145;は、JavaScriptのコードの一部として見えます。この式を順に解説していきます。

  1. p/9|0: これは、pを9で割った結果を整数に変換しています。具体的には、p/9の小数部分を切り捨てる操作を行います。|0はビットワイズOR演算子で、この文脈では小数点以下を切り捨てるために使用されています。

  2. *(p/9|0)145: 上記で整数に変換した結果を145倍します。つまり、pが9で割り切れる度に145が加算されるということを意味します。

  3. p*A: pとAという2つの変数または定数を掛け合わせた値です。

  4. **C[i]=pA-(p/9|0)145: この式全体では、pとAの積から、(p/9|0)*145を減算した結果を配列Cのi番目の要素に代入しています。

この式は、特定の計算を高速に行うためのテクニックを使用している可能性があります。145という数字の具体的な意味や背後にある理論は、与えられた情報だけでは判断できませんが、コードの文脈や目的に応じて特定の操作や変換を行っている可能性があります。

GTP4に聞いてみる

GPT5に期待したい

Gtp4oさんに聞く

コード内の145という数字は、テトリスの回転処理に関連する数値のようです。この数字の具体的な意味を理解するためには、コードの回転処理部分を詳しく見てみる必要があります。以下に該当部分のコードを再度示します。

for (C = [q = c = i = 4]; f = i-- * KEY; c -= !Z[h + (KEY + 6 ? p + KEY : C[i] = p * ROW - (p / 9 | 0) * 145)]) p = B[i];

この部分では、`145`という数字が以下の式の中で使用されています。

C[i] = p * ROW - (p / 9 | 0) * 145

この式を分解してみると、

  1. `p * ROW` - `p`の位置に基づいて、行の位置を計算しています。

  2. `(p / 9 | 0)` - `p`を9で割り、ビットOR操作で整数部分を取得しています。

  3. `* 145` - この数値を掛けることで、特定の変換を行っています。

テトリスのブロック回転では、通常、現在のブロックの位置を中心に90度回転させます。このとき、新しいブロックの位置を計算するための補正が必要です。この`145`という数値は、その補正値である可能性が高いです。特に、特定のブロック形状やその回転によって、新しい位置がどのように決定されるかに影響する補正値です。

145の可能な意味

  • 補正値: 回転によってブロックの位置を補正するための特定の定数として使用される。

  • ブロック形状の特性: 特定のブロック形状（例：L字型、T字型など）に対して適用される補正値。

実際にこの数値の正確な意味を知るには、テトリスの回転アルゴリズムの詳細な設計や他の部分のコードも見て総合的に判断する必要がありますが、上記の説明が一般的な解釈になります。

GPTo1にも聞いてみる

なぜ 145 なのか

145 という数値自体は、フィールドの幅（12）やミノの配置パターン（特に 3×3 や 4×4 のグリッド）に関連しています。以下の点が考えられます。

  • フィールド内の位置関係:

    • フィールドは一次元配列で表現されているため、二次元座標を一次元インデックスに変換する必要があります。

    • 145 は、この変換や回転時の位置補正に適した値として選ばれています。

  • 数式の最適化:

    • コードゴルフでは、コードの文字数を減らすために数式を極限まで簡略化します。

    • 145 を使用することで、複雑な計算を簡潔に表現でき、コード全体のサイズを削減できます。

まとめ

145 は、テトリスのブロック回転時に各ミノの新しい位置を計算するための重要な定数です。フィールドのサイズやブロックの形状、位置補正の必要性など、複数の要因を考慮して導出された値であり、この値を用いることで効率的に回転処理を実現しています。

書き換えていく


https://editor.p5js.org/setapolo/sketches/mYB5Zxpam


https://editor.p5js.org/setapolo/sketches/XMy0rnvBV
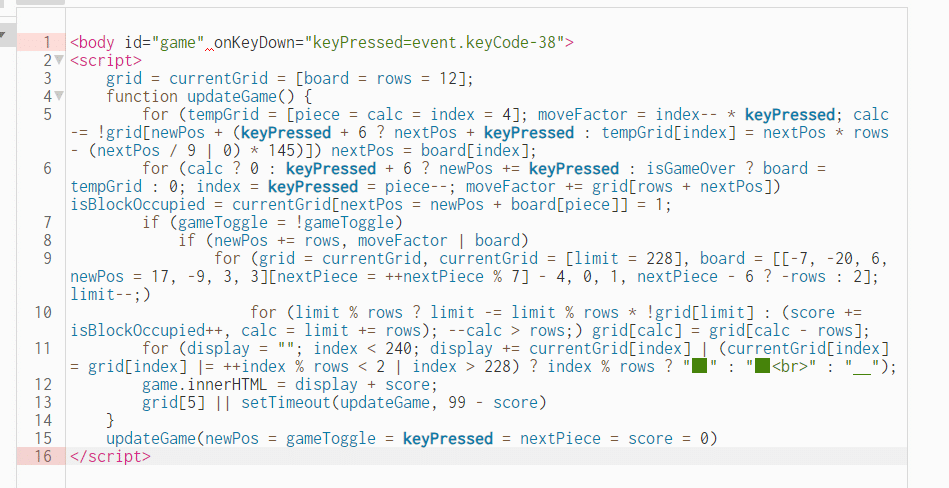
    grid = currentGrid = [board = rows = 12];
    function updateGame() {
        // ピースの移動計算: キー操作に応じてピースを移動させる。計算にはピースの位置、キー入力、グリッドの状態が使われる。
        for (tempGrid = [piece = calc = index = 4]; moveFactor = index-- * keyPressed; calc -= !grid[newPos + (keyPressed + 6 ? nextPos + keyPressed : tempGrid[index] = nextPos * rows - (nextPos / 9 | 0) * 145)]) {
            nextPos = board[index];
        }
        // ゲーム状態の更新: 新しいピース位置を確定し、キー入力後のゲーム盤の状態を更新する。
        for (calc ? 0 : keyPressed + 6 ? newPos += keyPressed : isGameOver ? board = tempGrid : 0; index = keyPressed = piece--; moveFactor += grid[rows + nextPos]) {
            isBlockOccupied = currentGrid[nextPos = newPos + board[piece]] = 1;
        }
        // ピースの配置とスコア計算: 新しいピースを配置し、行が完成していればそれを消去してスコアを加算する。
        if (gameToggle = !gameToggle) {
            if (newPos += rows, moveFactor | board) {
                for (grid = currentGrid, currentGrid = [limit = 228], board = [[-7, -20, 6, newPos = 17, -9, 3, 3][nextPiece = ++nextPiece % 7] - 4, 0, 1, nextPiece - 6 ? -rows : 2]; limit--;) {
                    for (limit % rows ? limit -= limit % rows * !grid[limit] : (score += isBlockOccupied++, calc = limit += rows); --calc > rows;) {
                        grid[calc] = grid[calc - rows];
                    }
                }
            }
        }
        // 表示更新: ゲーム盤の現在の状態をブラウザに表示する。各セルはブロックがある場合「■」、ない場合は「＿」で表される。
        for (display = ""; index < 240; display += currentGrid[index] | (currentGrid[index] = grid[index] |= ++index % rows < 2 | index > 228) ? index % rows ? "■" : "■<br>" : "＿") {
            // このループ内では特に追加のロジックは不要
        }
        game.innerHTML = display + score;
        // ゲームの継続判定: ゲームが続くべきかどうかを判断し、必要なら次の更新をスケジュールする。
        if (!grid[5]) {
            setTimeout(updateGame, 99 - score);
        }
    }
    updateGame(newPos = gameToggle = keyPressed = nextPiece = score = 0)
// ゲームのグリッドを初期化
初期化 グリッド、現在のグリッド、ボード、行数 = 12

// ゲームの状態を更新する関数
関数 更新ゲーム():
    // ピースの移動計算
    初期化 一時的グリッド
    繰り返し (各ピースに対して):
        計算新しい位置
        更新一時的グリッド
        
    // ゲーム状態の更新
    繰り返し (新しいピースの位置を確定):
        更新グリッド
        
    // ピースの配置とスコア計算
    もし 行が完成していれば:
        行を消去
        スコアを加算
        
    // ゲーム盤の表示を更新
    初期化 表示
    繰り返し (全てのセルに対して):
        表示更新
        
    // ゲーム盤をブラウザに表示
    ブラウザに表示(表示 + スコア)
    
    // ゲームの継続判定
    もし ゲーム続行条件を満たすなら:
        次の更新をスケジュールする

// ゲーム開始
更新ゲーム()

解説

  1. グリッドの初期化: ゲームのメイングリッドと現在のグリッドが初期化されます。これらはゲームの状態を追跡するために使われます。

  2. ピースの移動計算: ユーザーのキー操作に基づいて、ピースを新しい位置に移動させる計算を行います。この計算は、現在のピースの位置、入力されたキー、そしてグリッドの状態を使用して行われます。

  3. ゲーム状態の更新: 新しいピースの位置を確定し、グリッドを更新します。これには、キーボード入力やゲームオーバーの条件もチェックされます。

  4. ピースの配置とスコア計算: ピースを配置し、完全な行があればそれをクリアしてスコアを加算します。これはテトリスの基本的なゲームメカニズムです。

  5. 表示の更新: ゲームのグリッドの現在の状態を更新して、ブラウザに表示します。各セルは、ブロックが存在するかどうかに応じて異なる記号で表示されます。

  6. ゲームの継続判定: ゲームが続行可能かどうかを判定し、継続可能であれば次の更新をスケジュールします。

お願い致します