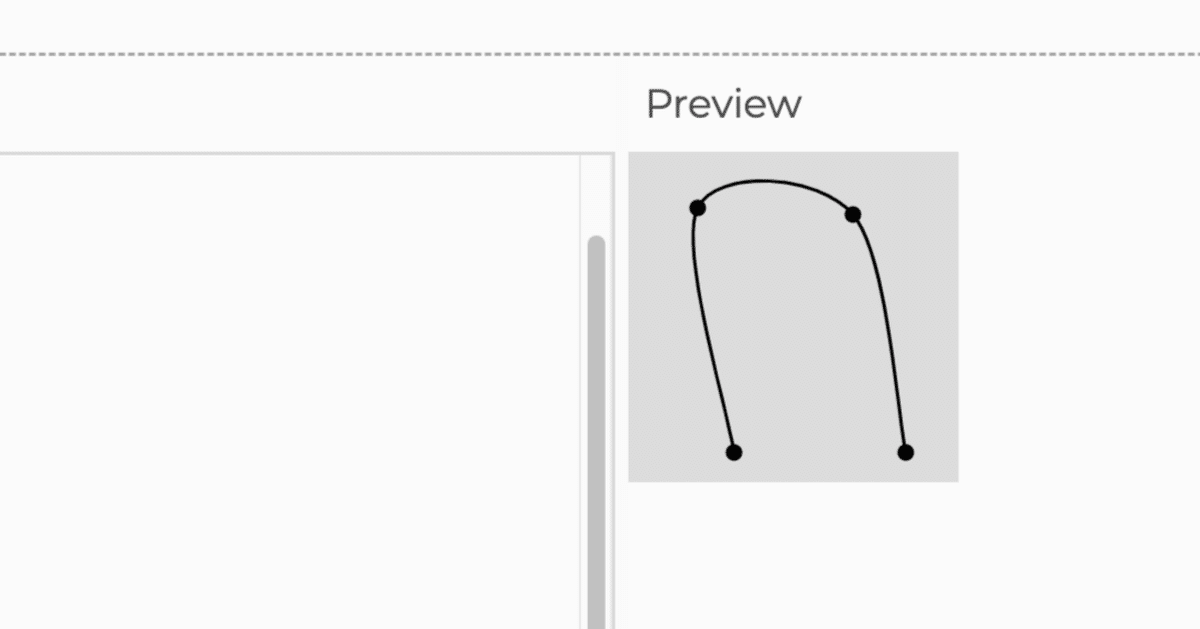
🎡p5.js curveVertex()のサンプル
curveVertex()関数は、Catmull-Romスプラインの実装です。
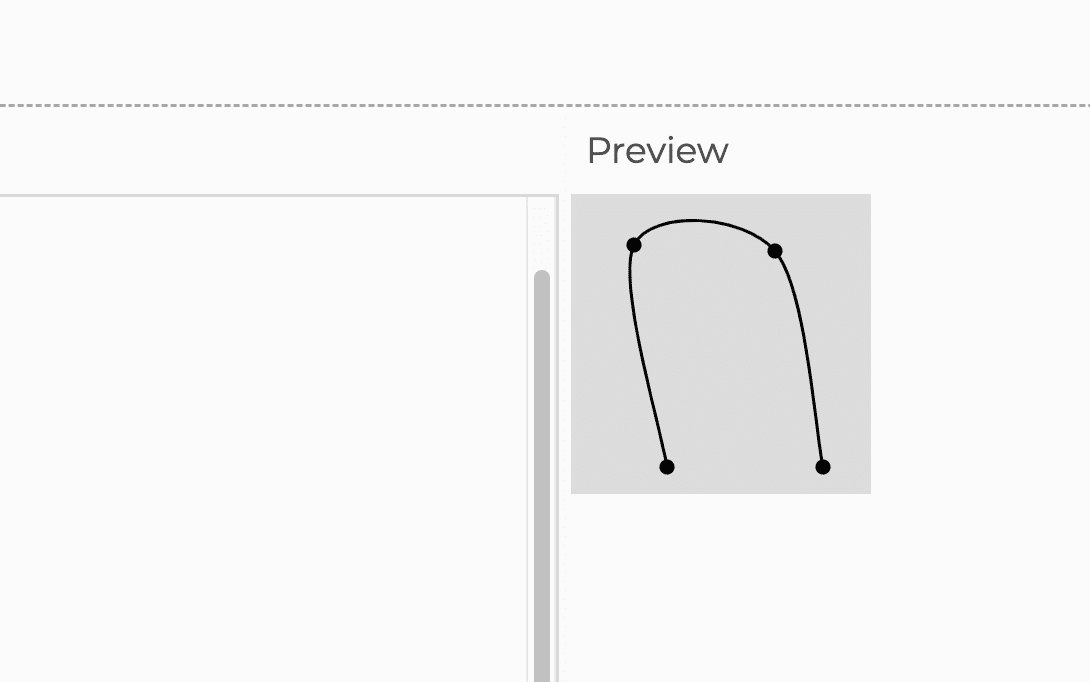
Edwin CatmullとRaphael Romにちなんで命名されたこの曲線は、元の点群に沿った点がスプライン曲線の制御点にもなることが最大の利点である[5]。一様なCatmull-Romの実装では、ループや自己交差が発生することがあります。コンピュータグラフィックスでは、キーフレーム間のスムーズな補間モーションを得るために、Catmull-Romスプラインが頻繁に使用されます。例えば、離散的なキーフレームから生成されるカメラパスアニメーションの多くは、Catmull-Romスプラインを用いて処理されています。Catmull-Romスプラインは、比較的簡単に計算でき、各キーフレームの位置が正確に当たることが保証され、さらに生成された曲線の接線が複数のセグメントに渡って連続していることが保証されていることが人気の理由です。
コンピュータビジョンでは、求心性Catmull-Romスプラインを用いて、セグメンテーションのためのアクティブモデルを構築している。アクティブスプラインモデルと呼ばれている[4] このモデルは、アクティブシェイプモデルをベースに考案されているが、求心性のあるCatmull-Romスプラインを用いて連続する2点を結合することで(アクティブシェイプモデルは単純な直線を用いる)、形状を描くのに必要な点の総数を少なくしているのが特徴である。
立方体多項式スプラインは、コンピュータグラフィックスやジオメトリックモデリングにおいて、平面や3次元空間の特定の点を通る曲線や運動軌跡を得るために広く用いられている。三次多項式スプラインは、オイラー・ベルヌーイの梁理論などの構造解析にも広く用いられている。
この関数は、beginShape() と endShape() の間、および beginShape() に MODE パラメータが指定されていない場合にのみ使用できます。WebGL モードでは、curveVertex() は 3D モードだけでなく 2D モードでも使用できます。2D モードでは 2 つのパラメータを、3D モードでは 3 つのパラメータを指定します。
一連のcurveVertex()線の最初と最後の点が、曲線の始まりと終わりのガイドとして使用されます。2点目と3点目の間に小さな曲線を描くには、最低4点が必要です。curveVertex()で5点目を追加すると、2点目、3点目、4点目の間に曲線が描かれる。
スプライン曲線:
スプライン曲線は、一般的に「区分的に定義される多項式曲線」として表されるものです。
スプラインは、複数の制御点を通る曲線として生成されますが、それぞれの区間で異なる多項式で定義されることが一般的です。
この曲線の有名なタイプとして「Bスプライン」や「NURBS」があります。
スプライン曲線の主な特徴として、滑らかさを維持しながら曲線を構築できる点が挙げられます。
ベジェ曲線:
ベジェ曲線は、定義に用いる制御点の位置に基づいて、特定の数学的定義(ベジェの定義)に従って形成される曲線です。
ベジェ曲線は、制御点によって形状が決まり、これらの制御点を動かすことで曲線の形を変えることができます。
この曲線の特性として、始点と終点は制御点の最初と最後の点を通るが、その他の制御点は必ずしも曲線上を通るわけではない点が挙げられます。
ベジェ曲線の最も基本的な形は、2つの制御点を持つ線形ベジェ、3つの制御点を持つ2次ベジェ、4つの制御点を持つ3次ベジェなどがあります。
いいなと思ったら応援しよう!

