
📏対数と乗数 不確定性と純粋度
情報理論が確率の対数を利用する理由が知りたいです
情報理論における確率の対数の利用は、情報量の定量化に関連しています。具体的には、情報量を測るために確率の対数が用いられる理由にはいくつかの重要なポイントがあります。
情報の加算性: 対数を使用することで、独立したイベントから得られる情報量は、それぞれのイベントの情報量の和として表現できます。例えば、二つの独立したイベントがそれぞれ確率 p と q で発生する場合、これらのイベントが同時に発生する確率は pq となります。対数を取ると、この同時発生の情報量は log(pq)=log(p)+log(q) となり、各イベントの情報量の和に等しくなります。これにより、情報の処理が数学的に扱いやすくなります。
直感的な情報量の表現: あるイベントの確率が低いほど、そのイベントが発生したときに得られる情報量は大きくなります。対数を使うことで、この直感を数式で表現できます。確率が低いイベント(つまり、予測しにくいイベント)は、高い情報量を持つと考えられます。
非負の情報量: 対数関数は、0より大きい値に対してのみ定義されており、情報量を非負の値として扱います。これは、情報量を実用的に扱う上で直感的かつ便利です。
情報理論の基礎: クロード・シャノンによって確立された情報理論の中心的な概念であるエントロピーは、確率変数の不確実性や乱雑さを測る尺度です。エントロピーは、システム内の各状態の確率の対数を用いて計算され、この形式は情報の不確実性を定量化するのに適しています。
これらの理由から、情報理論では確率の対数を利用して情報量を定義し、エントロピーの計算などに使用しています。このアプローチにより、情報の不確実性や情報量を数学的に扱うことが可能になります。
ジニ不純度という確率を乗数であらわす尺度もあると聞きました。これは上記の理由にあてはまらないですか?
ジニ不純度は、確率を乗数で表現する尺度であり、情報理論で用いられる対数を使った尺度(例えばエントロピー)とは異なる目的で使用されます。ジニ不純度は、特に決定木などの機械学習アルゴリズムでクラス分けの不純度を測るために用いられます。
ジニ不純度の計算式は以下の通りです。
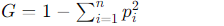
ここで、piは、クラス iに属するサンプルの割合です。
ジニ不純度は、データセット内のクラスがどれだけ混在しているかを測る尺度であり、この値が低いほど、データセットが純粋(つまり、同じクラスのサンプルで構成されている)であることを示します。一方、高い値はデータセット内のクラスが多様であることを示します。
ジニ不純度が情報理論のエントロピーと異なる点は、エントロピーが情報の不確実性や乱雑さを測るのに対し、ジニ不純度は分割後のデータセットの純粋度を直接測ることにあります。エントロピーが対数を用いる理由は、情報量の加算性や直感的な情報量の表現、非負の情報量の保証などに基づいていますが、ジニ不純度はより直接的にデータセットの純粋度を測定するために設計されています。
したがって、ジニ不純度は上記の対数を利用する理由とは異なる目的で使用される尺度であり、特にデータの分割の純粋度を評価する文脈で有用です。
純粋度の尺度で乗数を使い、不確定においては対数を利用する、といった一般的な計算傾向があるのでしょうか?
純粋度の尺度に乗数を用い、不確実性の尺度に対数を用いる、というのは一般的な傾向として捉えることができますが、これはその数学的特性と実用上の便宜に基づくものです。各尺度が選択される背景には、特定の目的や望ましい性質があります。
純粋度の尺度に乗数を使用する理由:
直接的な理解: 純粋度の尺度(例えばジニ不純度)は、データセット内のクラスの分布がどれだけ均一かを直接的に測定します。乗数を使用することで、クラスの分布が純粋(一つのクラスのみ)である場合に最小値(例えばジニ不純度では0)を、分布が均等(クラスが完全に混在)である場合に最大値を取ります。この性質は、決定木の分岐点を決定する際など、分割の純粋度を直感的に理解しやすくするために役立ちます。
不確実性の尺度に対数を使用する理由:
情報の加算性: エントロピーのような不確実性を測る尺度は、独立したイベントからの情報量が加算できるという性質を持っています。この性質は、対数を使用することで達成され、情報理論の基本的な原則となっています。
直感的な情報量の表現: 対数を使用することで、確率が低い(予測しにくい)イベントが高い情報量を持つという直感を数式で表現できます。
結論:
これらの傾向は、数学的な便宜と、特定の問題に対する直感的な理解を深めるための選択に基づいています。純粋度を評価する際には、その直接的な測定が求められるため乗数が用いられ、不確実性や情報量を評価する際には、対数を用いてその性質を反映させることが一般的です。しかし、これらの選択は絶対的なものではなく、特定のアプリケーションや目的に最も適した尺度を選択することが重要です。
いいなと思ったら応援しよう!

