
📏加重平均の計算ステップ
加重平均は、各データ点に異なる重みをつけて平均を計算する方法です。通常の算術平均では、すべてのデータ点が等しく扱われますが、加重平均では一部のデータ点が他のデータ点よりも「重要」と見なされ、その重要性に応じて重みが割り当てられます。これにより、データの集合における特定の要素の影響を調整することができます。
加重平均の計算式は以下の通りです。
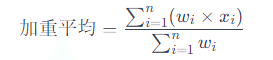
ここで、xi はデータ点の値、wi はそのデータ点の重み、n はデータ点の総数です。
例えば、テストの成績を計算する際に、中間テストが30%、期末テストが70%の重みを持っているとすると、これらのテストの加重平均を取ることで、全体の成績を算出することができます。
加重平均は、経済学、金融学、統計学など、さまざまな分野で利用されます。特に、異なる市場の指標を統合したり、特定の要因により影響を受けやすいデータセットを分析したりする際に有用です。
values = [10, 20, 30] # データ点の値
weights = [1, 2, 3] # 各データ点の重み
weighted_average = sum(w * v for w, v in zip(weights, values)) / sum(weights)
print(weighted_average)
Σ(シグマ)を使用せずに加重平均を示す具体的な例をいくつか挙げましょう。これらの例では、加重平均の概念がどのように異なる形式で表現されるかを示します。
1. 確率的な事象の加重平均
確率的な事象における期待値は、事象の結果とその確率の加重平均として計算されます。たとえば、コイン投げで表が出る確率が0.5、裏が出る確率も0.5とすると、期待値は次のように簡単に表現できます。
期待値(E)=(1×0.5)+(0×0.5)=0.5期待値(E)=(1×0.5)+(0×0.5)=0.5
ここでは、1は「表」が出た場合の「利得」、0は「裏」の場合の「利得」を表しています。
2. 線形結合による加重平均
線形結合を用いた加重平均は、特に線形代数や機械学習モデルのコンテキストで見られます。例えば、2つの特徴量�1,�2x1,x2に対する加重和は、各特徴量に重みw1,w2を掛けて加算することで計算されます。
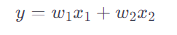
この式では、yは加重平均を表し、シグマ記号は使用されていません。
3. 強化学習における価値推定
強化学習の文脈では、新しい情報を元にした状態価値関数や行動価値関数の更新が、Σを使わずに行われます。例えば、簡単なTD(0)更新では次のようになります。
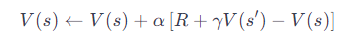
ここで、V(s)は現在の状態の価値、αは学習率、Rは報酬、γは割引率、V(s′)は次の状態の価値です。この式は、新しい観測からの情報を現在の価値推定に組み込む方法を示しており、Σを使用していません。
4. 投票や意思決定における加重平均
特定の選択肢に対する加重平均得点を計算する場合、各選択肢に対する評価得点とその重要性(重み)を乗算し、合計します。例えば、2つの選択肢があり、それぞれの得点が5と4、重みが3と2であれば、加重平均は次のように計算できます。
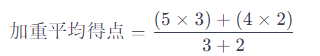
この式は、加重平均を計算する際にシグマ記号を使用していませんが、各項目の重み付けを考慮しています。
加重平均の計算ステップを以下の擬似コードで説明します。
function calculateWeightedAverage(values, weights) {
// Step 1: 初期化
weightedSum = 0
totalWeight = 0
// Step 2: 各値とその重みを使って加重和と重みの合計を計算
for i from 0 to length(values) - 1 do
weightedSum = weightedSum + (values[i] * weights[i])
totalWeight = totalWeight + weights[i]
end for
// Step 3: 加重平均を計算
weightedAverage = weightedSum / totalWeight
// Step 4: 結果を返す
return weightedAverage
end functionこの擬似コードのステップは次の通りです:
`weightedSum`(加重和)と `totalWeight`(重みの合計)を初期化します。
`values` 配列の各要素と対応する `weights` 配列の要素を掛け合わせて `weightedSum` に加算し、同時に `totalWeight` に `weights` の要素を加算します。
`weightedSum` を `totalWeight` で割ることで、加重平均を計算します。
計算結果の加重平均を返します。
いいなと思ったら応援しよう!

