📏相加平均の解説

相加平均（算術平均）は、一連の数値の合計をその数の総数で割った値です。これは、データセット内の数値の中心的傾向を測定する最も基本的な方法の一つです。相加平均を求めるには、以下の手順に従います。

1. すべての数値を合計する。

2. 合計を数値の個数で割る。

たとえば、データセットが 4, 8, 6 の場合、相加平均を求める手順は以下の通りです。

1. 数値の合計を求めます: 4+8+6=184+8+6=18

2. 合計を数値の個数（この場合は 3）で割ります: 18÷3=618÷3=6

したがって、このデータセットの相加平均は 6 です。

相加平均は非常に一般的で理解しやすい方法ですが、外れ値（非常に高い値や非常に低い値）の影響を受けやすいという欠点もあります。外れ値が存在する場合、中央値やモード（最頻値）など他の中心傾向の尺度も参考にすることが推奨されます。

• n はデータセットにおける数値の個数です。

• xi​ はデータセットにおける各数値を表し、i は 1 から n までのインデックスです。

• ∑∑（シグマ）記号は、続く xi​ の合計を i=1 から n まで計算することを意味します。

例えば、3つの数値 4, 8, 6 の相加平均をこの式で計算すると、

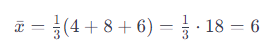
となり、先ほど説明した計算方法と同じ結果が得られます。シグマ記号を使用すると、数値のリストが長くても、より簡潔に合計を表現することができます。