
大気の不安定の程度がわかる天気図
今回は、大気の状態が不安定な領域を示す天気図をGSMのGPV(GRIB2形式)を利用し作図していきます。
最後に、実行可能なサンプルコードを添付します。コードの説明では、わかりやすくするために、コードの一部を切り出しています。そのままでは動作しまません。ご留意ください。
大気成層の不安定域について
この不安定の程度を示す物理量(例えばSSIやCAPE)や、対流不安定など成層の大気の安定度の考え方は様々あります。ここではシンプルに、下層で最も相当温位が高い気塊を、上層の気圧面(300hPaなど)まで断熱過程で持ち上げ、環境場とこの気塊の気温差を求めることにします。気塊の温度の方が高いと潜在不安定と言えます。この気温差が大きいほど不安定となります。
図には、この気温差の分布に、不安定に上層の寒気が影響しているかわかるように、上層の気圧面の気温の等値線を重ねて示すこととします。
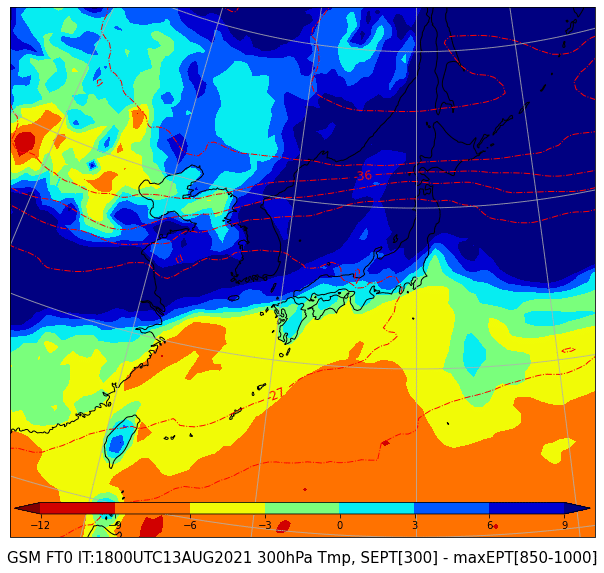
(シェードは、300hPaの飽和相当温位 - 850から1000hPaでの相当温位の最大値。
赤点線は300hPaの気温)
複数の気圧面のデータの読み込み
下層の相当温位最大値を取得するために、下層の上端の気圧面を指定する必要があります。下のコードでは、この気圧の変数をpreLowとしています。また、上層の気圧面の変数は、preTopとします。
pygribでは必要な気圧面を一括して読み込めて便利です。grbs()関数の中で、次のpythonのラムダ式(無名関数)を使って、読み込む気圧面を指定しています。
level=lambda l: l >= preLow or l == preTop
要素は、高度と気温、相対湿度を読み込んでいます。
import pygrib
import xarray as xr
import numpy as np
#
# 一部省略
#
# データOpen GSMのGRIB2ファイル名を指定
grbs = pygrib.open(data_fld + gr_fn)
#
# データ読み込み。 要素毎に、tagHpの等圧面から下部のデータをいっきに読み込みます。
# 高度
grbHt = grbs(shortName="gh",typeOfLevel='isobaricInhPa',
level=lambda l:l >= preLow or l == preTop)
# 気温
grbTm = grbs(shortName="t",typeOfLevel='isobaricInhPa',
level=lambda l:l >= preLow or l == preTop)
# 相対湿度
grbRh = grbs(shortName="r",typeOfLevel='isobaricInhPa',
level=lambda l:l >= preLow or l == preTop)3次元データセットの作成
必要な物理量を計算するため、GPVデータをMetPyに適したxarrayを使ったデータセットに変換します。
下のコードの流れは、格子数や気層数を取得し、3次元データ化するために必要な配列を準備し、読み込んだデータをその配列に入力することでデータセットを作成していきます。適宜コメント行を入れています。ご確認ください。
このように、作成したデータセット(変数名:ds)を使うと、簡単に物理量を算出できるようになります。
## grbデータの3次元データ化
# GPVの緯度・傾度の1次元配列 の 取得
lats2, lons2 = grbHt[0].latlons()
lats = lats2[:,0]
lons = lons2[0,:]
#
# GPVのレベルの配列 の 取得
levels = np.array([g['level'] for g in grbHt])
indexes = np.argsort(levels)[::-1]
#
# GPVの2次元データの格子数 の 取得
x, y = grbHt[0].values.shape
#
# 要素毎の3次元データの配列作成と0に初期化
cubeHt = np.zeros([len(levels), x, y])
cubeTm = np.zeros([len(levels), x, y])
cubeRh = np.zeros([len(levels), x, y])
for i in range(len(levels)):
cubeHt[i,:,:] = grbHt[indexes[i]].values
cubeTm[i,:,:] = grbTm[indexes[i]].values
cubeRh[i,:,:] = grbRh[indexes[i]].values
#
## 3次元データのDataset作成
ds = xr.Dataset(
{
"Geopotential_height": (["level","lat", "lon"], cubeHt * units.meter),
"temperature": (["level","lat", "lon"], cubeTm * units('K')),
"relative_humidity": (["level","lat", "lon"], cubeRh * units('%')),
},
coords={
"level": levels,
"lat": lats,
"lon": lons,
"time": [grbHt[0].validDate],
},
)
# 単位を指定
ds['Geopotential_height'].attrs['units'] = 'm'
ds['temperature'].attrs['units']='K'
ds['relative_humidity'].attrs['units']='%'
ds['level'].attrs['units'] = 'hPa'
ds['lat'].attrs['units'] = 'degrees_north'
ds['lon'].attrs['units'] = 'degrees_east'算出方法
下のコードでは、得られたデータセットに、露点温度・相当温位・飽和相当温位を計算し追加しています。
## 露点温度 計算
ds['dewpoint_temperature'] = mpcalc.dewpoint_from_relative_humidity(
ds['temperature'],ds['relative_humidity'])
ds['dewpoint_temperature'].attrs['units']='K'
## 相当温位 計算
ds['ept'] = mpcalc.equivalent_potential_temperature(
ds['level'] * units('hPa'), ds['temperature'], ds['dewpoint_temperature'])
ds['ept'].attrs['units']='K'
## 飽和相当温位 計算
ds['sept'] = mpcalc.saturation_equivalent_potential_temperature(
ds['level'], ds['temperature'])
ds['sept'].attrs['units']='K'下層の最大の相当温位を求めるコードは次の通りです。便宜上、最下層の等圧面に、下層の最大の相当温位を入力していきます。この処理は、かなりの時間がかかります。今後、高速化できる手法を検討したいです。
## ds['ept'][0]に、ds['ept'][下層]の最大値を代入する !!!
# 計算処理遅い高速化必要!
for i in np.arange(len(levels) - 2):
print(i)
for j in np.arange(len(lats)):
for k in np.arange(len(lons)):
e0 = ds['ept'][0].values[j][k]
e1 = ds['ept'][i+1].values[j][k]
if (e1 > e0):
ds['ept'][0].values[j][k] = e1サンプルコード
描画部分は、これまでの記事と同様なため、説明は省きます。下から、上記のコードを含む、実行可能な Jupyter Notebook用のコードをダウンロードできます。入力用のGSMのGRIB2ファイルはご用意ください。
これまでの8回の記事を理解できれば、これらを少し応用することで、多くのタイプの数値予報天気図を作成できると思います。番外編の記事では、MetPyについて調べるためのリンク集を掲載しています。基本的なものが多いですが、参考になれば幸いです。
次回の内容は、等渦位面天気図についてです。
