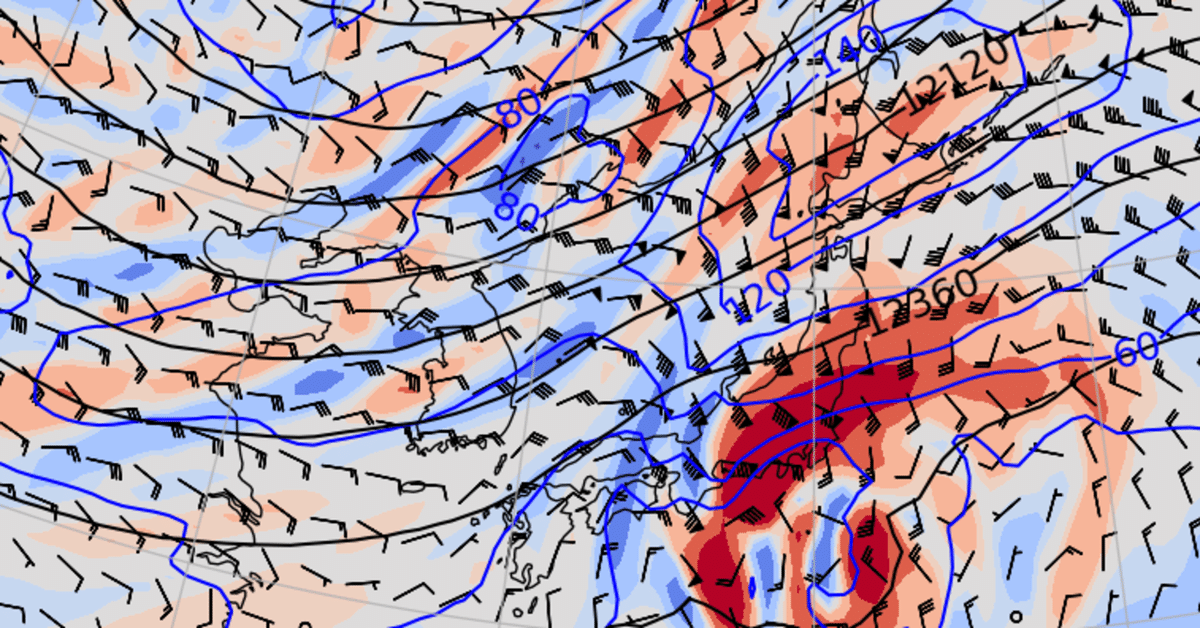
ジェット気流と上層発散を把握できる天気図

2021年10月9日 20:44

今回は、ジェット気流の簡単な説明と、ジェット気流の風速の状況などがわかる天気図の作図コードの紹介です。作成する天気図はMetPyを利用し、ジェット気流の位置と速さ、収束発散、非地衡風成分を図示します。記事の最後に、コード(Jupyter Notebook用)を添付しておきます。ご活用ください。

ジェット気流について

ジェット気流ついては、気象庁ホームページに掲載されている教科書「総観気象学基礎編」の3章に詳しく解説されています。

ジェット気流の位置や曲率、トラフ、リッジの解析は、低気圧の発達・衰弱のステージを把握したり、前線帯の構造や位置の解析に重要です。また、ジェット気流に伴う上層発散は積乱雲の発達に寄与し、上層収束は積乱雲の衰弱に寄与します。

ジェット気流の入口の暖気側や出口の寒気側では一般的に上層発散が生じています。その範囲は発散域から確認し、ジェット気流の加速や減速に対応する非地衡風成分の風も確認することで、適切な診断ができるでしょう。このため、後で紹介する天気図では、非地衡風成分を図示することにしました。

ジェット気流を確認するための天気図は200hPa面や300hPa面の天気図が基本となっています。しかし、200hPaと300hPa面で収束と発散の分布が異なったりする場合もあります。力学的圏界面天気図や鉛直断面図の解析も利用して、圏界面付近の気象状況を総合的に把握してください。

ジェット気流を把握するための天気図の作成について

ジェット気流の位置などを把握するための天気図の作成について紹介します。この天気図の作成コードは、Python言語でMetPyライブラリを使っています。記事「GSMの500hPa面天気図作成」には、このライブラリを使った天気図作成の基本が書かれています。この記事を読んでおられない方は、まずこの記事を確認いただいて、以下を読んでください。ここでは共通する部分のコードの説明は省略し、変更点・追加点のみとしています。

非地衡風成分の算出

　前回紹介した地衡風成分の算出と同じで、次のような流れとなります。
　　① GRIB2ファイルを読み込み
　　② MetPyの物理量を算出する関数を利用するためのデータセットの作成
　　③ 非地衡風や収束発散の算出

### 表示するデータなどの指定
# GSMの読み込む初期値の年月日時をUTCで与えます。
i_year =2021
i_month = 10
i_day = 3
i_hourZ = 12
#
# 予想時間を与える。この値は注意が必要です。下3桁目が日数、下２桁で時間で与えます。
#  初期値なら0、18時間後なら18、24時間後なら100、36時間後なら112となります。
i_ft = 200
#
#  時間に変換
ft_hours=int(i_ft/100) * 24 + int(i_ft%100)
#
# Jetを解析する気圧面を指定
tagHp = 300
#
# 描画する範囲の大まかな指定
i_area = [115, 151, 20, 50]  # 日本付近
#
## GPVの切り出し領域の指定：(lonW,latS)-(lonE,latN)の矩形                                                                                                      
latS=-20
latN=80
lonW=70
lonE=190
#
# データの格納先フォルダー名
##!!! GRIB2データの保存先をFolderを指定すること !!!
data_fld="/Users/hogehoge/Data/gsm/"
#
###　データの読み込み
# 読み込むGRIB2形式GSMのファイル名
gsm_fn_t="Z__C_RJTD_{0:4d}{1:02d}{2:02d}{3:02d}0000_GSM_GPV_Rgl_FD{4:04d}_grib2.bin"
gr_fn= gsm_fn_t.format(i_year,i_month,i_day,i_hourZ,i_ft)
#
# データOpen
grbs = pygrib.open(data_fld + gr_fn)
#
# データ取得                                                                                                                       
grbHt = grbs(shortName="gh",typeOfLevel='isobaricInhPa',level=tagHp)[0]
grbWu = grbs(shortName="u",typeOfLevel='isobaricInhPa',level=tagHp)[0]
grbWv = grbs(shortName="v",typeOfLevel='isobaricInhPa',level=tagHp)[0]
#
# データClose
grbs.close()
#
print(gr_fn)
#
# データ切り出し                                                                                                                   
valHt, latHt, lonHt = grbHt.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
valWu, latWu, lonWu = grbWu.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
valWv, latWv, lonWv = grbWv.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
#
## 非地衡風算出のためにxarrayデータセットを作成                                                                                   
ds = xr.Dataset(
  {
      "Geopotential_height": (["lat", "lon"], valHt),                                                                        
      "u_wind": (["lat", "lon"], valWu),
      "v_wind": (["lat", "lon"], valWv),
  },
  coords={
      "level": [tagHp],
      "lat": latHt[:,0],
      "lon": lonHt[0,:],
      "time": [grbHt.validDate],
  },
)
# 単位も指定する
ds['Geopotential_height'].attrs['units'] = 'm'
ds['u_wind'].attrs['units']='m/s'
ds['v_wind'].attrs['units']='m/s'
ds['level'].attrs['units'] = 'hPa'
ds['lat'].attrs['units'] = 'degrees_north'
ds['lon'].attrs['units'] = 'degrees_east'
#
# metpy仕様に変換
dsp= ds.metpy.parse_cf()
#  
### 物理量の算出
# 風速
dsp['wind_speed'] = mpcalc.wind_speed(dsp['u_wind'],dsp['v_wind'])
# 地衡風計算　平均処理した高度から求める
dsp['uag'], dsp['vag'] = mpcalc.ageostrophic_wind(dsp['Geopotential_height'],
                            dsp['u_wind'],dsp['v_wind'])
# 収束発散                                                                               
dsp['conv'] = mpcalc.divergence(dsp['u_wind'],dsp['v_wind'])
#
# knotsへ変換
dsp['wind_speed'] = (dsp['wind_speed']).metpy.convert_units('knots')
dsp['uag'] = (dsp['uag']).metpy.convert_units('knots')
dsp['vag'] = (dsp['vag']).metpy.convert_units('knots')

矢羽の描画コード

2次元の風を矢羽で描画するコードは、下の通りです。全ての格子点で矢羽を表示すると見にくくなるため、表示する格子点を間引くことで見やすい図を作ることができます。どの程度間引くかを指定する際は、slice()関数を使います。(前回の記事Q ベクトルの矢印表示の時と同じです。)

矢羽描画関数 barbs()で指定している pivot は、格子点と矢羽の描画位置関係を指示しています。矢羽の風向を示す線分において、その中点を格子点中央位置とする場合は"middle"を、矢羽の風向を示す線分の先端とする場合は"tip"(これがdefault)と指定します。

## 非地衡風 矢羽:データを間引いて描画   
# 2次元データを間引くための設定　x,y座標共に　3格子点に1点 表示する                                                      
wind_slice2 = (slice(None, None, 3), slice(None, None, 3))
# 1次元データを間引くための設定 3格子点に1点 表示する 
wind_slice0 = slice(None, None, 3) 
# 風の矢羽を描画する  lengthで矢羽の長さを設定                       
ax.barbs(dsp['lon'][wind_slice0], dsp['lat'][wind_slice0],
        dsp['uag'].values[wind_slice2], dsp['vag'].values[wind_slice2], 
        length=5.5,
        pivot='middle', color='black', transform=latlon_proj)

サンプルコード

説明したコードは作図コードの一部のみとなっています。次のファイル(Jupyter Notebook用)に全てのコードを掲載します。このコードを使って、300hPa面や200hPa面の天気図作成を試してみてください。

次回は、鉛直断面図を表示するコードを紹介します。

この記事が気に入ったらサポートをしてみませんか？