
水の温度上昇から太陽の表面温度を求める方法について
こんにちは。バーチャル理科教師の西薗です。
前回【自由研究】暑すぎるので水で太陽の温度を測ってみたという記事を書いたところ、noteの特集ページに取り上げて頂くなどありがたい反響を頂きました。
しかしながら当該記事は、わかりやすさ重視のために説明が省略された点がいくつかあります。
そこでなるべく疑問や誤解を残さないよう、この記事では省略された計算やより正確な理論について解説していきます。
① シュテファン=ボルツマンの法則について
前回の記事ではシュテファン=ボルツマンの法則について紹介しました。

記事では"I"のことを一貫して「光エネルギー」と呼んできましたが、実はこの物理量は「エネルギー」ではなく、正確には「放射源表面から1秒・1平方メートルあたりに放射される輻射エネルギー」を指します。
物理学界隈ではこれを「エネルギーフラックス (Energy Flux)」と呼ぶことが多いですが、「放射発散度」と呼ばれることもあるようです。

記号に"I"が使われるのは、近い意味の物理量である「放射強度(Intensity)」の頭文字を使った名残かと思われます。
記事では本当は「エネルギーフラックス」のものを「光エネルギー」と呼んでいたから、単位が「ジュール」ではなく「ワット毎平方メートル」だったんですね。
どうですか? ついてきてます?
「どうでもいいよ、結局はエネルギーだろ」と思いませんか?
なんでこんな細かいことをダラダラと決めなければいけないのかというと、物理学っていうのは「出来上がったお味噌汁を見て作り方を考える」ような学問だからです。
作り方を考えるにはどんな食材をどう加工して、どんな調理をしたのかを考えなければなりません。
そのためには、「光エネルギー」という刻みネギではなく、「エネルギーフラックス」という長ネギ1本まで戻してやらなければ作り方が理解できないのです。
学校の物理の問題で「空気抵抗はないものとする」「糸の重さは0とする」などと書いてあるのはこのためです。
「加熱とか出汁とか置いといて、とりあえず具材を混ぜたら同じ見た目になるのか見てみましょうよ」っていうのが目的なんです。
この例えで言うと、工学は「知っている食材や調理法を使って理想のスープを作る」学問と言えるでしょう。私の感覚では理学と工学の違いはこんな感じです。
話が逸れましたが、「公式の記号が何を表しているか」を理解するのは非常に重要なことです。これを勘違いしていると、せっかく実験しても本来と全然違う結果になってしまいますからね。
② ジュールからワット毎平方メートルへの変換
記事では、実験で求めたエネルギー量を何の説明もなしに時間で割ったり面積で割ったりしました。これは何をしていたかというと、単位を「ジュール」から「ワット毎平方メートル」に変換していたんですね。

なぜこんな変換をする必要があるのかというと、水の温度変化から求められるのは「エネルギー(単位:ジュール)」なのに対して、シュテファン=ボルツマンの法則に当てはめられるのは「エネルギーフラックス(単位:ワット毎平方メートル)」だからです。
ワットは「ジュール毎秒」という意味なので、水の温度変化から得られたエネルギー量を測定時間で割ってやれば、水が何ワットでエネルギーを受け取っていたかがわかります。
そしてこのワット数を「面積(単位:平方メートル)」で割ってやれば「ワット毎平方メートル」になるわけですが、この面積というのは何の面積なのかというのが重要です。
ここで、太陽表面から出た光が断熱容器に届くまでのざっくりの図を考えてみます。

さて、この図の"黄色い円筒"を通ってきた光だけが断熱容器に入って水の温度変化に関わるわけですが、実験ではこの円筒の中を1秒あたり2.31ジュール相当のエネルギーの光が通っているということを突き止めたのでした。
この「時間あたり2.31ジュール」に「面積あたり」を加えるには、当然この「円筒の断面積」で割ってやればいいわけです。
円筒の断面積を求めるには円筒の半径が必要なわけですが、これは測定することができません。なぜならこんな円筒は目には見えないからです。
そこで、上の図をもっとシンプルにしてみましょう。
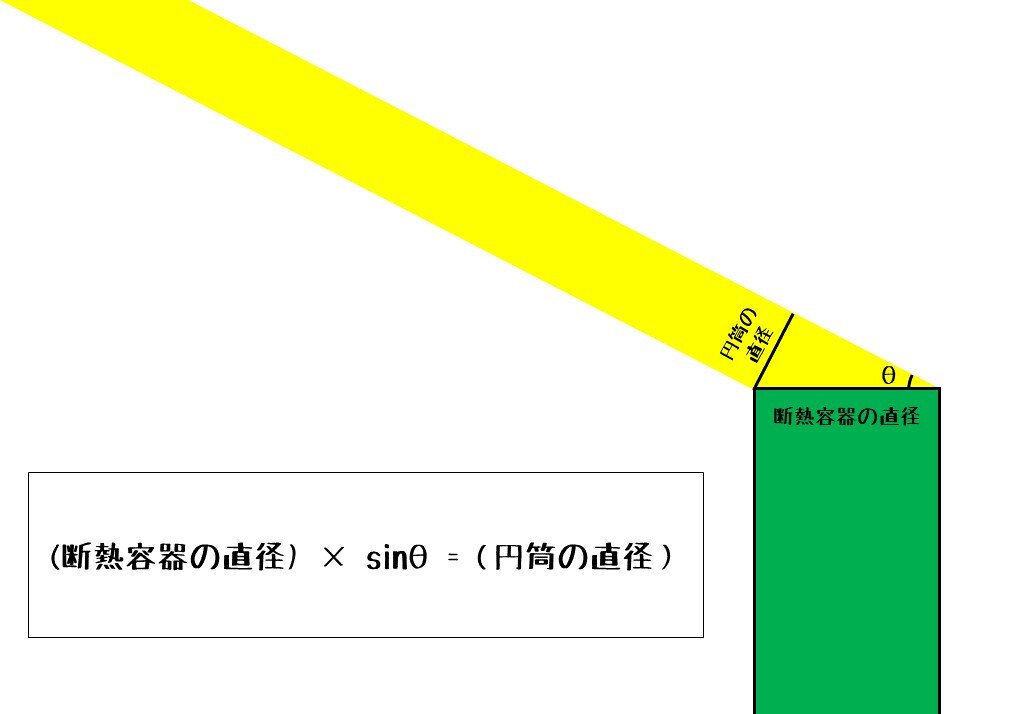
なんということでしょう。
断熱容器の直径と光の入射角θがわかれば、三角比を使って円筒の直径がわかるではありませんか。
断熱容器の直径は定規を当てて測定できます。約7cmでした。
また、光の入射角θは太陽の高度に相当します。
測定を行ったのは日が最も高くなる時間の前後30分程度なので、実験当日の南中高度を当てはめれば良さそうです。
国立天文台の暦計算室によれば、当日の南中高度は74.5°とのこと。
よって、円筒の直径は7×sin74.5°=6.75cm。半径は3.37cmです。
つまり円筒の断面積は3.37×3.37×3.14=35.7cm^2となります。
これを平方メートルに直すと0.00357m^2となります。
以上より、「水が1秒・1平方メートルあたりに受け取ったエネルギー」は
2.31 ÷ 0.00357 = 647 W/m^2
となるわけです。
ちなみにこの物理量は「放射照度」と呼ばれており、「エネルギーフラックス」と同じ単位を持っています。
両者の違いは「受け取る側」か「出す側」かの違いだけです。これは水が受け取った=照らされたエネルギーなので「放射照度」というわけですね。
③ 距離による光の減衰について
さて、単位を揃えることには成功したわけですが、シュテファン=ボルツマンの法則に当てはめられるのは「エネルギーフラックス」であるため、今求められた「放射照度」では当てはめられないわけです。
「放射照度」を「エネルギーフラックス」に変換するために、記事では「距離による光の減衰」と「地球表面での反射」について補正を加えたのでした。
記事では「太陽の表面から放射された光は、地球に到着するまでに約0.00218%にまで減衰する」と書いたのですが、この数字は別に天文学の常識とかそういうわけではないです。(地球の反射能0.3は惑星科学の常識に近いかもしれませんが)
このパーセンテージは私の計算結果を書いたに過ぎません。
ここではその計算過程について解説します。
まず、太陽から地球にどのように光が届くか考えてみましょう。
太陽と地球、そして太陽から出てくる光を図にしてみました。

この図の矢印は、太陽から放射される光を表しています。
光が太陽の中心から放射状(互いが交差しないよう)に出てくるとすると、地球に届く光は先程と同様に、"黄色い円筒"を通ってきた光だけということになります。
円筒の中を通る矢印の数を見てみると、太陽の表面では5本くらいの矢印が収まっていますが、そのうち地球まで届いているのは1本だけです。
つまり太陽表面と地球とを比較すると、地球での「面積あたりの光のエネルギー」が少なくなっているんですね。
これが「距離による光の減衰」です。
では、「面積あたりの光のエネルギー」がどのくらい少なくなるのかを計算してみます。
とりあえず、太陽表面を通過する面積あたりの矢印の本数と地球表面を通過する面積あたりの矢印の本数の比を求める方向で計算してみます。
光はまっすぐしか進めないので、放射源(ここでは太陽の中心)を中心とした球を考えると、球全体の表面を通過する矢印の本数は球の半径によらず変わらないはずですね。
ということは、球面を通過する矢印の面積あたりの本数は、
(矢印の総数)÷(球の表面積)
で求められるはずですね。
球の表面積は (半径)×(半径)× 4 × 3.14 で求められます。
ここでは太陽表面での本数と地球に届いた時点での本数を比較したいので、前者の球の半径は太陽の半径=約700000000m、
後者の球の半径は太陽と地球の平均距離=約150000000000mとなります。
よって表面積は前者が約6160000000000000000m^2、
後者は約283000000000000000000000m^2 となります。
減衰の割合を求めるには、「(矢印の総数)÷(太陽から地球までを包む球の表面積)」を「(矢印の総数)÷(太陽の表面積)」で割ってやればいいわけです。
「矢印の総数」はここで約分されるので、わからなくても計算できます。
つまり、
6160000000000000000 ÷ 283000000000000000000000 = 0.0000218
となるわけです。
これが、太陽表面から地球に辿り着くまでに残っている光の割合になります。
記事では、これと地球の反射能の分とを補正することで、「放射照度」を「エネルギーフラックス」に変換していた、ということだったんですね。
おわりに
というわけで、難しい話はここまでです。お疲れ様でした。
可能な限り数学を抜きにして書いてみましたが、いかがでしたでしょうか。
恐らくですが、「わかりやすかった」とは感じにくいと思います。
なぜなら、普段なら記号や略記を使えば済むところを日本語や数字で長々と記述しており、頭の中で情報の整理がしにくいからです。
数学というのは定量的な関係性を表すのに非常に優れた言語なんですね。
数学が苦手な人の多くは、日本語と数式と図との翻訳で躓いてしまっている印象があります。
もちろん今後も実験や解説の記事・動画は数学よりも日本語を使って説明していこうと思いますが、難しい内容を扱おうとするほど今回の記事のようになります。
そこをどうわかりやすくできるか考えて工夫するのがバーチャル理科教師としての務めかと思っております。
長々と語りましたが、とりあえずこの2つだけ覚えて頂ければ結構です。
① 物理学は「出来上がったお味噌汁を見て作り方を考える学問」
② 数学は「定量的な関係性を表すのに非常に優れた言語」
ここまで読んで頂きありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
