個性爆発！〜6/22やってみる研究室 #21【いろんな形、なかま分けしてみる？】イベントレポ〜

2024年6月22日にやってみる研究室 #21【いろんな形、なかま分けしてみる？】を開催しました👏

テーマは「図形」。折り紙を折ったり、厚紙を切ってパズルをつくったりする、幼稚園生から楽しめるプログラムです。個性あふれた工作の様子をお裾分けします！

やってみる研究室（みる研）とは？

「日常の謎を見つけて、なんでもやってみる！」をコンセプトに2022年5月にスタート。研究学園都市つくばの特徴を活かしつつ、よりいろいろ「やってみる」体験をお届けします！

部屋の中でしきつめをさがそう！

まずはかたちをさがしてみるところから。5分間でたくさんのしきつめが見つかりました！

靴箱の板！

イベント情報の時間枠も長方形のしきつめになっている！

本棚の木枠もしきつめ！

ソファの布も縦糸と横糸でしきつめられている！こんな小さいものまで…

本の中にもしきつめがある？！

かたちについて知ろう！

次に、見つけたかたちの特徴を調べます。「ぱったんのかたち（鏡像対称/線対称の図形）」「ぐるぐるのかたち（回転対称の図形）」になかま分けしてみました。

ぱったんのかたちとぐるぐるのかたち

ハートはぱったんのかたち、正三角形はぐるぐるのかたちでもありぱったんのかたちでもある

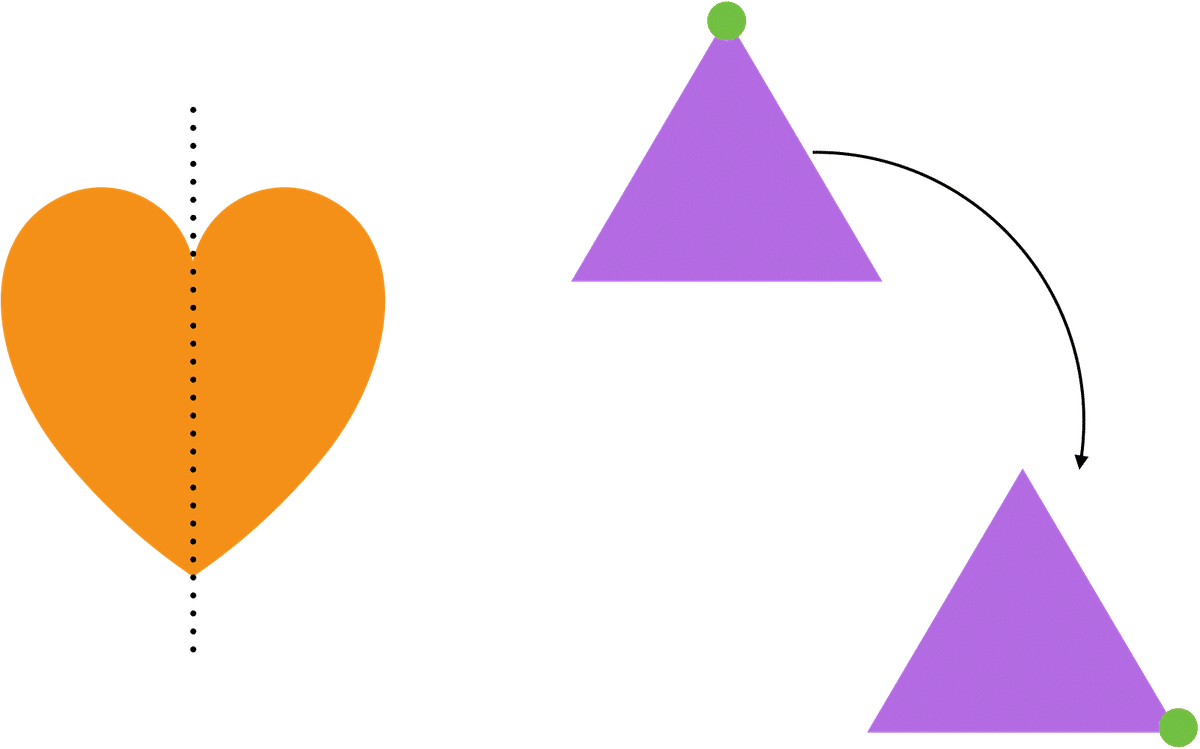
おりがみでかたちをつくろう

次は、自分で「ぱったんのかたち」と「ぐるぐるのかたち」をつくってみます。色とりどりの折り紙を切ったり折ったりしながらたくさんの作品ができました！

思い思いのかたちをつくります

立体の折り紙を折った子も！

折り紙に顔や絵を描いた参加者もいました！

つくったかたちはぱったんのかたちかな？ぐるぐるのかたちかな？

ぜんぶ同じかたちのパズルをつくろう！

これまでにわかったかたちの特徴を使って、厚紙でパズルをつくります！

ドットの入った工作用紙にかたちを描いていきます

きれいにハサミで切ります

まだ真っ白のパズルを切ったとおりに並べることに挑戦！

切ったパズルに絵を描いて完成！

対称性と研究

最後に、いろいろな学問で使われている対称性について紹介しました（ちょっと難しいけれど、大人の参加者もいたのでちょっと詳しめに。）例えば、平面のくりかえし模様は「対称性」で分類すると17種類あることがわかっています（参考）。化学の分野では、原子が規則正しく並んだ「結晶」を使った研究について対称性が関連しています（参考）。

私の専門である素粒子物理では、対称性は「保存則」を導きます。例えば、宇宙が回転対称性（今回は扱っていない）を持つこと、つまり空間のどこでも物理法則が変わらないということから運動量保存則を導くことができます。

対称性と保存則の関係

学校で習ったエネルギー保存則や運動量保存則は当たり前だと思っていたけれど、もっと根本の考え方があることに物理のおもしろさを感じた、というエピソードを話しました。

ご参加いただいたみなさん、この記事を読んでくださったみなさん、ありがとうございました！

ゆーみるしー