When the angle is very small, sinΘ can be approximated to Θ
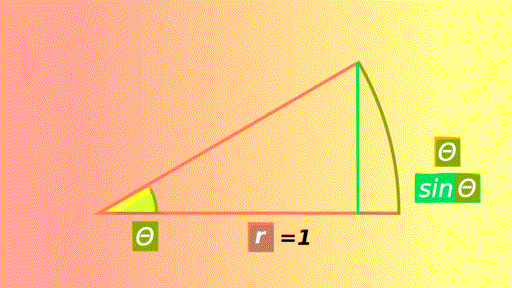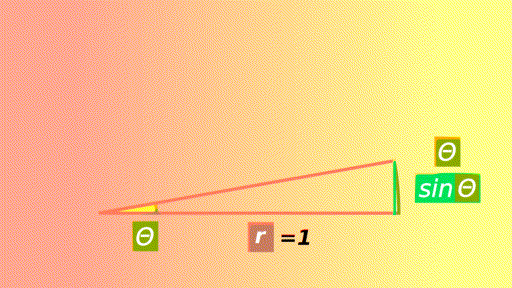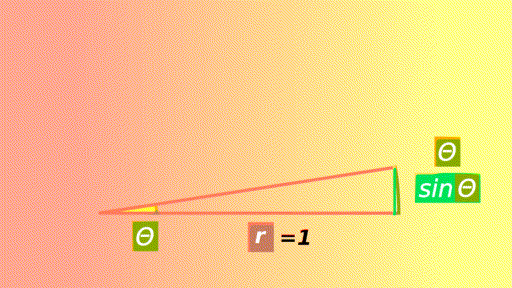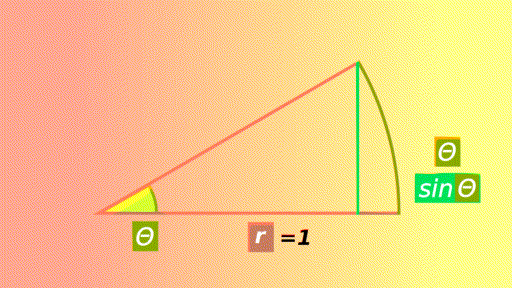
In the previous article on centripetal force, sin Θ was approximated to Θ when the angle was very small.
Why can sinΘ approximate Θ when the angle is so small?
Radians represent the angle of the arc
The angle in "radians" represents the length of the arc of the circle.
The smaller the angle, the closer the value of sinΘ is to the arc length Θ.
When the arc length of the circle is Θ, the angle is Θ [rad].
In other words,
The length of the arc "itself" is the angle [rad]
The way of expressing the angle is different from the 360 degree method.
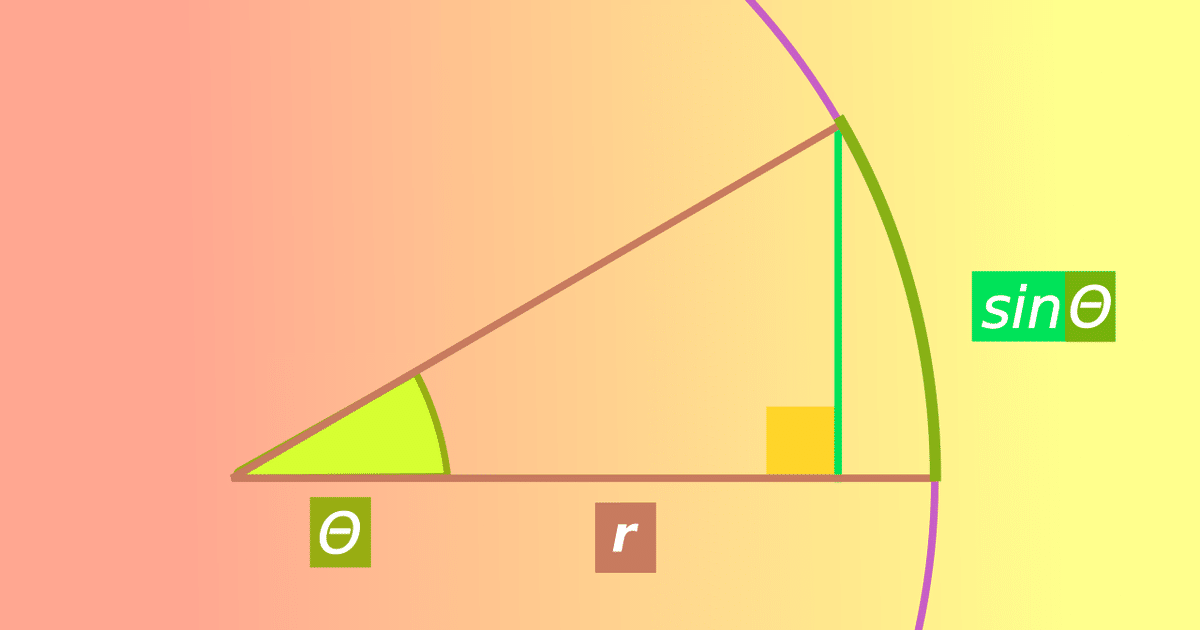
Trigonometric function : sinΘ
The value of the trigonometric function sinΘ is dropped from one radius of the sector to the other at right angles.
The smaller the angle, the closer the value of sinΘ is to the arc length Θ. Check it with the above animation.
The arc length Θ becomes the angle Θ when the unit of angle is radians.
l = r × Θ = ΘSummary
- sinΘ can be approximated to Θ when Θ is small
- The arc length Θ is "almost" the same as sinΘ
- The unit of angle is radians
- Radians represent the angles that make up the arc
