
Radian - ラジアン - 弧度法
ラジアンは、円弧 に対する 角度

前回は、角度が とても小さいとき のことを書きました。
近似した 円弧の長さ Θ が、sin(Θ) と "ほぼ" 同じになるのは、
角度Θ が ラジアンの場合です。
今回は その ラジアンについて。
ラジアンは、円の弧から見た 角度 です。
だから 日本語で 弧度 法。

例えば 半径 r = 1 を そのまま円周にのせます。
その時の角度 が 1 [ラジアン]。
360度法

円を 360で分ける 度数法 は、直感的。
ラジアンの本質

半径 1 の 円 で 確認

弧の長さ 1 のとき、角度は 1 [rad]

弧の長さ 2 のとき、角度は 2 [rad]
2 [rad] のとき、円弧の長さは 2

弧の長さ 3 のとき、角度は 3 [rad]
3 [rad] のとき、円弧の長さは 3

弧の長さが 3.1415... は、半円
ラジアンで表す角度は、π [rad]
π [rad] (3.1415..) のとき、円弧の長さは π
π は 円周率です。
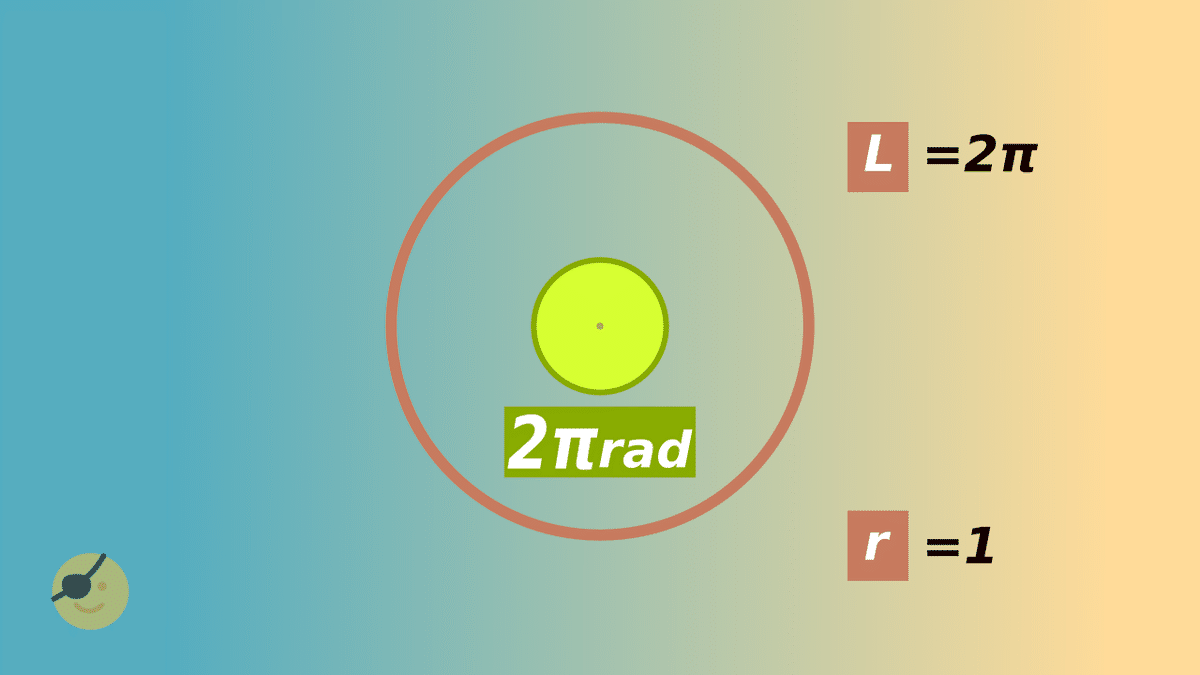
円周の長さ 2 π は真円。 角度は 2 π [rad]
2π [rad] のとき、円弧 真円 の長さは 2π
美しいラジアン
Q: なぜラジアンを使うの?
A: 楽だから
円の特徴 を、
度数法の 360 や、円周率 π を使わずに
簡単に 表せます。
Q: 例えば?
A: 円弧の長さ
円弧の長さ を l とすると
Θ を ラジアン で考えると、
l = r Θ
Θ を 度 で考えると、
l = (2 π / 360) r Θ
A: 扇型の面積
Θ を ラジアン で考えると、
S = 1/2 r^2 Θ
Θ を 度 で考えると、
S = π / 360 r^2 Θ
360° と rad の 関係
角度は、弧度法でも、度数法でも 表せます。
ただ、視点が違うのです。
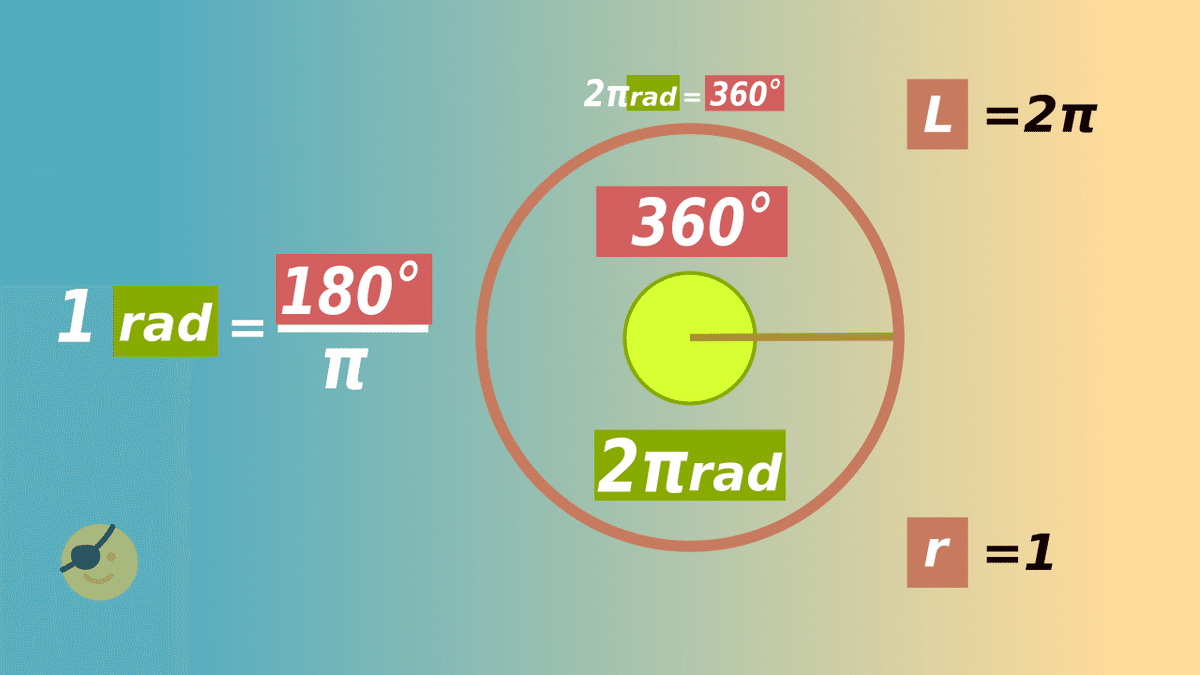
真円の角度は、弧度法でも、度数法でも 同じで、
弧度法で、 2π [rad]
度数法で、 360°
2π [rad] = 360°
1 [rad] = 180° / π
おまけ : Radius - 半径

Radian は、
2つの半径 (2 radii) に挟まれた、
"弧を作る角度" という意味です。
Radian は、19世紀の工学者 James Thomsonによって、使われたという説もありますが、、。実は、17-18世紀、ニュートンと交流のあった Roger Cotes によって、すでに使われていたようです。
radius は、ラテン語で 円の半径です。
半径が 1つ は 、 1 radius です。
半径が 2つ あると 、 2 radiuses ではありません。2 radii 、、。
複数形は なぜか radii、、、。英語圏では ラディアイ と発音します。( らでぃい ではありません )
radius、radial, radii, radian, など、みんな 半径に関係しています。小耳にはさむ言葉に radius が隠れていることがあります。例えば、ラジアルタイヤ、 ラジアル荷重、ラジアルデザイン、ラジアルアンテナ、ラジアルアキシャル、、。

たとえば Radial Tire は、タイヤの骨組みが、半径方向に配置されている構造なのですね!
まとめ
- ラジアンは 円弧 に対する 角度 を表す
- 弧度法 の 角度 は、円の弧 との対応
- 半径1の円の 半径を 円の弧に 置いてみる と、感覚的にわかりやすい
- ラジアンを使うと、円の特徴をシンプルに 表せる
もともとは、
もともとは、ジャンクギターの弦が切れて、弦のテンションをまとめようと思ったら、巡り巡って、ラジアンに行き着いてしまいました。
