
アンテナファクタとゲインの関係式とその導出
アンテナファクタ$${A_f}$$とゲイン$${G_a}$$は以下の関係式となる。
本稿にその導出方法をまとめる。
$$
A_f=\frac{2\pi}{\lambda}\sqrt{\frac{120}{G_aR_I}}=\frac{2\pi}{\lambda}\sqrt{\frac{2.4}{G_a}}
$$
※$${R_I}$$はシステムインピーダンス。(50Ω)
アンテナファクタ
アンテナファクタは、以下の式の通り、アンテナが受ける受信電界強度$${E_r \ \text{[V/m]}}$$とアンテナが出力する電圧$${V_r \ \text{[V]}}$$の関係を示す係数である。
$$
A_f=\frac{E_r}{V_r} \quad \text{[1/m]}
$$
アンテナファクタは、アンテナの仕様書に記載されている。
以下に、ETS-Lindgren社の3115アンテナのスペックに記載されているアンテナファクタを示す。
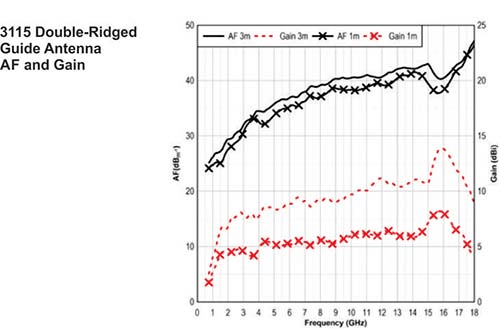
上図から分かるようにアンテナファクタは周波数特性を持つ。
冒頭で示した通り、アンテナファクタ$${A_f}$$とアンテナゲイン$${G}$$の関係式は以下の通りとなることから、アンテナファクタが周波数に依存することがわかる。※$${c=f\lambda}$$
$$
A_f=\frac{2\pi}{\lambda}\sqrt{\frac{120}{G_aR_I}}=\frac{2\pi}{\lambda}\sqrt{\frac{2.4}{G_a}}
$$
アンテナファクタとゲインの関係式の導出
冒頭の式を導出する。
パラメータは下図を参照のこと。

遠方界における、単位面積を通過する電磁エネルギー密度$${P_u}$$と電界$${E}$$の関係は、ポインティングベクトルの定理により下式の関係がある。ただし、電界は実効値。
※後述のポインティングベクトルの章を参照のこと。
$$
P_u=\frac{{E_r}^2}{120\pi} \quad[\text{W/m}^2]
$$
この電界強度$${E\ [\text{V/m]}}$$の空間に、有効開口面積$${A_e}$$のアンテナをおいた時の、アンテナの受信電力は$${P_r}$$は、下記式となる。
有効開口面積とは、アンテナのある位置で、電波のエネルギーをどの程度の面積で捉えているかを表す指標である。
$$
P_r=A_eP_u \quad[\text{W}]
$$
有効開口面積$${A_e}$$とアンテナ利得$${G_a}$$は、どんなアンテナでもその比は一定となる。その関係は以下の式で表される。
※下式の導出については、参考文献の「フリスの伝達公式」を参照のこと。
$$
A_e=\frac{\lambda^2}{4\pi}G_a\quad[\text{m}^2]
$$
以上の式より、アンテナの受信電力$${P_r}$$は以下の式で表される。
$$
P_r=\left( \frac{\lambda^2}{4\pi}G_a \right) \left( \frac{{E}^2}{120\pi} \right)
$$
アンテナ出力に接続された整合負荷$${R_I}$$で消費される電力$${P_o}$$は、インピーダンスマッチングが取れている場合、アンテナの受信電力$${P_r}$$と同等であることから、整合負荷における端子電圧を$${V_r}$$とすると、以下の式となる。
$$
P_o=\frac{{V_r}^2}{R_I}=P_r
$$
したがって、以下の式が成り立つ。
$$
\frac{{V_r}^2}{R_I}=\left( \frac{\lambda^2}{4\pi}G_a \right) \left( \frac{{E_r}^2}{120\pi} \right)
$$
アンテナファクタを導くため、下記のように式変形する。
$$
\left( \frac{{V_r}}{{E_r}} \right)^2=\left( \frac{\lambda^2}{4\pi}G_a \right) \left( \frac{R_I}{120\pi} \right)
$$
両辺の平方根の逆数は、下記の式となり、冒頭のアンテナファクタの式が導出できた。
$$
A_f=\frac{2\pi}{\lambda}\sqrt{\frac{120}{G_aR_I}}=\frac{2\pi}{\lambda}\sqrt{\frac{2.4}{G_a}}
$$
電界強度[dBuV/m]と電力[dBm]の関係式
これまでに得られた式から、電界強度と電力の関係式を導く。
まず、アンテナファクタの式の左辺がゲイン$${G_a}$$となるように変形すると、
$$
G_a=\left( \frac{2\pi}{\lambda A_f} \right)^2 \left( \frac{120}{R_I} \right)
$$
このゲインの式を、受信電力$${P_r}$$の式に代入すると、
$$
\begin{align*}
P_r&=\left( \frac{\lambda^2}{4\pi}\right) \left( \frac{{E}^2}{120\pi} \right)\left( \frac{2\pi}{\lambda A_f} \right)^2 \left( \frac{120}{R_I} \right) \quad \\ \\ &=\frac{{E_r}^2}{{A_f}^2 R_I}
\end{align*}
$$
したがって、受信電界強度$${E_r}$$と受信電力$${P_r}$$は以下の関係式となる。
$$
E_r=A_f\sqrt{R_IP_r}
$$
両辺を$${20\log_{10}}$$でとって、デシベル表記とすると以下の式となる。
$$
E_r \ \text{[dBuV/m]}=P_r \ \text{[dBm]}+A_f \ \text{[dB/m]} +107\ \text{dB}
$$
この式は、以下の記事で導出した結果と一致する。
ポインティングベクトル
本章では、単位面積を通過する電磁エネルギー密度$${P_u}$$が、ポインティングベクトルの定理から下式が導出されることを示す。
$$
P_u=\frac{{E_r}^2}{120\pi}\ [\text{W/m}^2]
$$
ポインティングベクトルは電磁波の持つエネルギーの流れの密度を表す物理量である。電磁波は平面波として空間を伝播していく性質を持つが、ポインティングベクトルは電磁波の進行方向を指す。
ポインティングベクトル$${\bm{S}}$$は以下の式で表される。
$$
\bm{S=E\times H}
$$
ポインティングベクトルの定理は下記の通り表される。
$${u}$$は単位体積あたりの電磁場のエネルギー密度を表す。
$$
\frac{\partial u}{\partial t} + \nabla\cdot\bm{S}=0 \\ \quad \\
\text{※}u=\frac{1}{2}(\bm{E}\cdot\bm{D}+\bm{H}\cdot\bm{B}) \quad \text{[J/m}^3]
$$
この定理の式を体積分すると、下記のガウスの発散定理より、ポインティングベクトルの単位が$${[\text{W/m}^2]}$$であることが分かる。
$$
\iiint_V \nabla \cdot \mathbf{S}\ dV = \iint_{S} \mathbf{S} \cdot \mathbf{n}\ dS
$$
したがって、ポインティングベクトル$${\bm{S}}$$の絶対値が、単位面積を通過する電磁エネルギー密度$${P_u}$$そのものであることから、電界と磁界の外積の絶対値を求めれば良い。
$$
P_u=|\bm{S}|=|\bm{E}\times\bm{H}| \quad [\text{W/m}^2]
$$
遠方界における微小電流源による電界および磁界は下記の式で表される。
$$
\begin{align*}
E_\theta&=j \frac{IlZ_0k_0}{4\pi r} e^{-jk_0r}\sin \theta \\ \quad \\
H_\phi&=j \frac{Ilk_0}{4\pi r} e^{-jk_0r}\sin \theta \\
\end{align*}
$$
この式の導出方法は下記記事をご参照ください。
この式から分かる通り、空間のインピーダンス$${Z_0}$$を用いて、電界と磁界は下記の関係式であることが分かる。
$$
E_\theta=Z_0 H_\phi
$$
空間のインピーダンスは下記式で表される。
$$
Z_0=\frac{E}{H}=\sqrt{\frac{\mu_0}{\epsilon_0}} \cong 120\pi
$$
したがって、ベクトルポテンシャルの絶対値は以下の式で表される。
$$
|\bm{S}|=|\bm{E \times H}|=E_\theta H_\phi=\frac{{E_\theta}^2}{120\pi}
$$
以上から、電磁エネルギー密度$${P_u}$$が下記式の通り導出された。
※下式の$${E_r}$$はアンテナ受信電界強度を表す。($${r}$$方向の電界ではない。)
$$
P_u=|\bm{S}|=\frac{{E_r}^2}{120\pi}
$$
参考文献
受信アンテナの出力電力 Pr[dBm]から電界強度を計算する方法についてhttps://www.emc-ohtama.jp/emc/doc/013_emc_reference.pdf
フリスの伝達公式 ~その周辺の不思議を探る~
http://www.radio3.ee.uec.ac.jp/ronbun/TR-YK-040_Friis-Formula.pdf
謎解き電磁気学 第4章 電磁波
http://www.radio3.ee.uec.ac.jp/ronbun/EM_Wonderland_Chap_4.pdf
