
簡潔データ構造ってなに?
こちらの記事は、2020年3月31日にRetrieva TECH BLOGにて掲載された記事を再掲載したものとなります。
こんにちは。レトリバのリサーチャーの木村@big_wingです。レトリバでは学習アルゴリズムの高速化や低リソース化に取り組んでいます。今回から何回かに分けて簡潔データ構造について紹介していく予定です。 初回である今回は簡潔データ構造の概念について紹介します。
簡潔データ構造の書籍としてはNavarro氏の本、日本語で書かれたものとしては定兼氏の本と岡野原氏の本があります。
簡潔データ構造
簡潔データ構造(succinct data structure)は1989年にJacobsonによって初めて提唱され、以降多くの研究者によってビットベクトル、文字列、グラフなど様々な種類のデータに対して提案されてきました。 簡潔データ構造を大雑把に定義すると、
データ構造のサイズが小さい。
高速なクエリ処理が可能である。
といった2つの特徴を兼ね備えたデータ構造です。 一般的にデータを圧縮してデータサイズを小さくすると、データの復元が必要となりクエリ処理に時間がかかってしまいます。一方で高速なクエリ処理を行うためには追加で補助的なデータ構造が必要となり、データサイズが大きくなってしまいます。簡潔データ構造はこれら計算時間とデータサイズのいいとこ取りをしよう!というデータ構造です。
次に簡潔データ構造を定量的に、もう少し厳密に定義するために必要な概念として、 「Word RAMモデル」と「情報理論的下限」を紹介します。またこれ以降lgn=log2nとします。
Word RAMモデル
簡潔データ構造を扱う際には、空間計算量をより厳密に解析するためにWord RAMと呼ばれる計算モデルを用いることが多いです。Word RAMモデルとは以下の仮定が成り立つ計算モデルです。
メモリはwビットのワードの配列から成る。問題の入力のサイズnに対してw≥lgnである。
連続するwビットのメモリ読み書き、四則演算、剰余、論理演算、シフト、比較が定数時間で可能。
初見で1つ目の仮定のw≥lgを見ると、ワード長が入力サイズに依存しているように見えて違和感を覚えるかもしれません。この仮定があると何が嬉しいのかというと、入力データに対してのランダムアクセスが可能となるという点です。n個のデータにランダムアクセスするためにはlgnビットからなるインデックスが必要となるため、1つ目の仮定は自然な仮定となっています。
2つ目の仮定で定数時間で行うことができる演算を定義しており、これを用いて簡潔データ構造の時間計算量を評価します。
情報理論的下限
簡潔データ構造を定量的に定義するにあたって情報理論的下限(information-theoretic lower bound)というものがあります。データ構造のサイズが小さいことが簡潔データ構造において重要な特徴であり、データ構造におけるサイズの理論的限界として情報理論的下限を定義します。
今、要素数がSである集合に対して情報理論的下限Lは L=lg⌈S⌉ビットと定義されます。 これは対象の集合の各要素が当確率で出現する時に、一つの要素を表現するのに必要なビット数に対応しています。出現に偏りがまったくないため、データ圧縮の観点から見ると最もデータを圧縮しにくい状態です。
このような最悪ケースにおいてこれ以上小さくすることができないというmin maxの意味で情報理論的下限という名前がついているのだと私は認識しています。
いくつか例を見てみましょう。
各要素が0または1の値をとる長さnの配列(ビットベクトル): 各要素が2通りの値を取り長さがnなので、この集合の要素数は2^nです。よって情報理論的下限はL=lg2^n=nビットとなります。
ノード数がnの順序木: ノード数がnの順序木は何個存在するでしょうか?結論だけ述べると、カタラン数と呼ばれる数
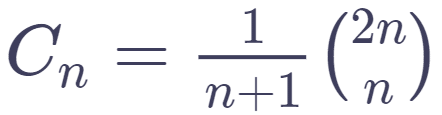
を用いて Cn−1と表現することができます。 よって情報理論的下限はL=2n−Θ(lgn)ビットとなります。(興味がある人は順序木の個数がカタラン数で表現できることを導出してみてください。順序木を深さ優先探索でトラバースし、入る時に-1、出る時に+1と対応付けるとランダムウォークのある条件を満たすパスの数え上げ問題に帰着されます。)
簡潔データ構造のもう少し厳密な定義
ここでは簡潔データ構造をもう少し厳密に定義します。最初に簡潔データ構造は、データ構造のサイズが小さく高速なクエリ処理が可能であるデータ構造であると述べましたが、これらをWord RAMモデルと情報理論的下限を用いて定義します。簡潔データ構造とは、
データ構造のサイズが情報理論的下限に漸近する。つまりデータ構造のサイズがL+o(L)ビット。
データに対するクエリの時間計算量が、Word RAMモデル上で従来のデータ構造と等しい。
の2つを満たすデータ構造であると定義します。ここで1つ目の条件のo(L)という表記は、Lが十分に大きい時にLと比べて無視できるほど小さいことを意味します。
データ構造のサイズが、最悪ケースの場合これ以上小さくすることができない情報理論的下限に漸近するということと、その上でクエリの時間計算量は従来のデータ構造と等しいということから簡潔データ構造が高速かつ省メモリであるということがわかります。
ここのタイトルでもう少し厳密な定義という煮え切らない表現をした理由は、2つ目の条件において、データに対するクエリの時間計算量がWord RAMモデル上で従来のデータ構造と等しいという曖昧な表現を用いているためです。例えば順序木であれば、従来のデータ構造とはポインタを用いた木構造の表現を想定していますが、従来のデータ構造を厳密に定義することはできません。
また、定義に述べた2つを満たさないデータ構造も簡潔データ構造とする場合もあります。例えば、従来のデータ構造ではクエリの時間計算量が定数時間であったものを入力サイズに依存したO(lnn)まで遅くなるものを許容したり、データ構造のサイズがO(lnL)であるものを許容するといったものです。
まとめ
簡潔データ構造の紹介の初回である今回は、簡潔データ構造の定義について紹介しました。定義については図を用いた直感的な説明を行うことが困難で、文字列の量が多くなってしまい申し訳ありません。今回のブログを読んでおもしろい!と感じられた方はぜひ最初に紹介した本を読んでみてください。定義だけを読んで興味を持たれた方はプロフェッショナルになれる素養があると思います。
次回以降では、ビットベクトル、文字列、木構造など具体的な簡潔データ構造を紹介していく予定です。
