
ひとり経営企画室の調査の基本(3)
縦棒グラフ
数値の情報は、グラフにすると視覚的にわかりやすくなります。よく使うグラフを紹介します。まずは縦棒グラフです。

2020年には前年より若干戻したものの2.9万戸まで減少した。
縦棒グラフは、時系列データを表現するときやデータの分布(ヒストグラム)を見るときに使います。ビジネスであれば、年度ごとの売上や利益をまず見ることになるので、縦棒グラフは使用頻度が最も高いのではないでしょうか。
この例であれば、伝えたいことは次の点になります。
2013年がピークであり、5.5万戸であった。
2013年から2020年にかけては年率8.8%で減少し、2.9万戸まで減った
2013年の前と後ろで、供給戸数に変化があったことがグラフの見た目だけで伝わるかと思います。また、変化の割合もグラフの高さの変化から感じることができますね。
このグラフを描くことで、次に調べる項目としては、どのような要因で2013年を境にして変化したのか?といったこともわかりますね。
横棒グラフ
次は横棒グラフです。まずは横棒グラフの例です。

しかし、その6カ月後には0.5%の増加に戻している。
商品・サービスといったアイテムを比較するときに横棒グラフは適していますね。
スライドは横長なので、横棒グラフを横に並べるといったこともできます。例にあげたように、グラフが時系列でどのように変化するのか?といった情報を表すときに使えますね。
最近のスライドはさらに横長になったので、この例よりも余裕を持って複数のグラフを配置することができることでしょう。
アイテムの順番も意識してグラフを作るとよいと思います。値が大きいもの、小さいものの順に並べるとか、普段見慣れている順序にする、など、いろいろ考えられますね。その中から伝えたい事に対して最適な順番を選んでください。
注目してほしいアイテムを強調することも大事です。そのアイテムの横棒だけを赤にする方法や他の横棒を薄めにして、注目してほしいアイテムだけ濃くする方法もあります。
大事なことは、
伝えたいメッセージは何か?
そのメッセージを伝えるのに最適なグラフは何か?
ということだと思います。
折れ線グラフ
棒グラフの次によく使うグラフは、折れ線グラフです。
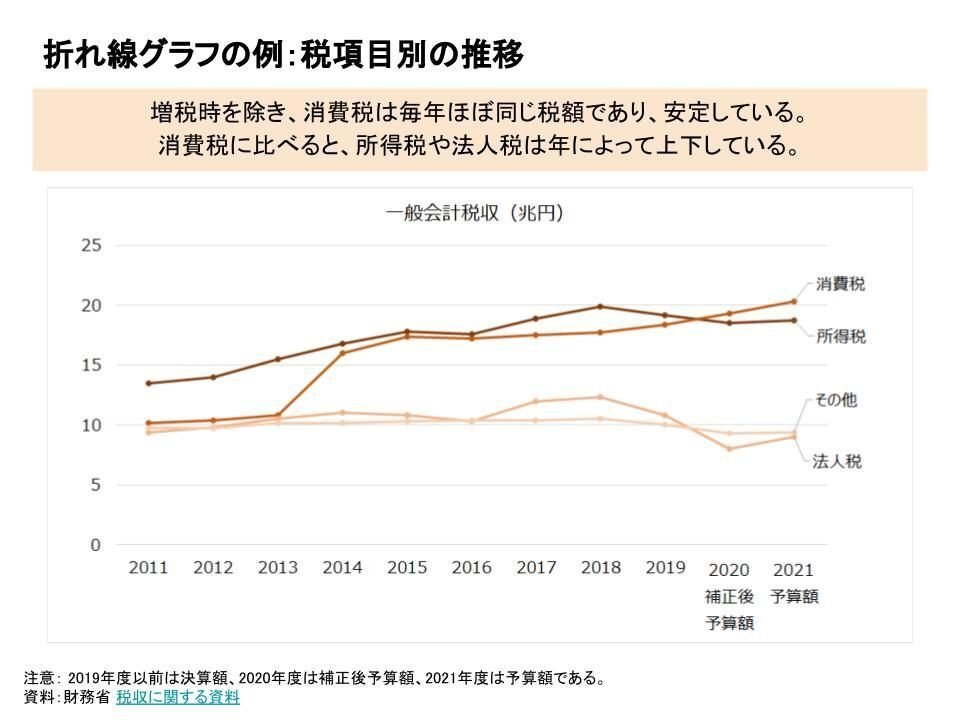
消費税に比べると、所得税や法人税は年によって上下している。
折れ線グラフは、1本だけではあまり魅力がありません。何本かを描いて、比較することで、伝えたいメッセージが強調されます。
この例であれば、伝えたいメッセージは「消費税は安定した主軸となる税項目である」だとします。消費税のグラフを1本描くだけでも、上下動の少ない安定したグラフにはなります。
それに加えて、所得税や法人税のグラフを描くことでまずは税収額の比較ができます。ここ2年、消費税は所得税を上回るほどの主軸の税項目であることが伝わりますね。
そして、これら所得税や法人税は上下動が見られます。それに比べて消費税は安定していることが、より分かりやすくなりますね。
折れ線グラフは、何本かを描くのがポイントです。
散布図
最後に紹介するグラフは、散布図です。このグラフは2つの値に相関関係があるときに描くグラフです。

しかし、F病院だけは平均から離れており、患者数の割に補助金が少ない。
この例では、コロナ受け入れ患者数が増えていくと、補助金額も増えていくという関係性を表しています。
相関があるからといって、因果があるわけではありません。しかし、この例では患者数に応じて補助金は出ていると思われるので、患者数の増加は、補助金の増加につながると言えるでしょう。
むしろ注目すべきなのは、関係性から外れているものです。この例であれば、F病院は患者数が多いにも関わらず、本来もらえると思われる補助金を受け取っていないと推測されます。背景にどのような要因があるのか、気になるところですね。
ここまで代表的なグラフを見てきました。まとめると以下のスライドのようになります。

円グラフも使うこともあるが、棒グラフで代用することもできる。
これまでに紹介しなかったものに、円グラフがあります。円グラフは内訳を示すときに使いますが、複数のアイテムの内訳を示して比較するのであれば、棒グラフを使う方がよいと思います。円グラフを使うのは、アイテムが1つのときだけが多いでしょう。
統計
定量的なデータに対して、統計学の手法を使うこともあります。使える場面として、特に次の2つが挙げられます。
関係性を探す
差があるか確認する
さまざまな手法がありますが、私が試したことがある手法をスライドにまとめました。

まずは、関係性を探す場面が挙げられます。自分で管理できる何かを増やしていく、あるいは、減らしていくと、売上や利益が増えていくといった関係性です。
例えば、自社の商品に対する値引き額を増やしていくと、増やすにつれて成約する確率は増えていくと思います。そのような関係性です。
値引きが増えるほど成約はしますが、利益は減ります。過去の販売データから値引きと成約率の関係性が見えてくれば、利益の視点で最適な値引き額を求めることができます。こういった関係性を探すときに統計手法が使えます。
また、ふたつの値に差が確かにあるかどうか確認するときにも統計手法が使えます。
例えば、商品紹介のサイトを2種類作り、それぞれでの販売個数に差があったとします。その差が統計的にも差があるかどうかを示すことができます。
そのような差は確率的によく起こることなのか、それともかなり珍しい確率でしか起きない差なのかを確認できるのです。
ただし、新規事業のようにデータの種類や量があまりない状況では、思ったようには統計手法を使うことができません。私もよく使ったのは、関係性を探す場面では相関と単回帰分析、統計的に差があるか確認する場面ではt検定とカイ二乗検定ぐらいです。
カイ二乗検定はExcel関数にはありませんが、それ以外はあります。Excel関数にある検定や相関、回帰分析ぐらいは試してみてもよいのではないでしょうか。

ただし、ロジスティック回帰はR言語を使うことになる。

割合の比較は直接求めることはできず、R言語を使うほうが簡単である。
Excelを使ったカイ二乗検定
調査をして二つのグループ間で見られた差が統計的に有意な差かどうかを知りたい場合があります。平均の差であればExcelでもT.TEST関数で簡単に計算できます。
しかし、割合の差の場合は、T.TEST関数のようには計算できません。R言語を使えば簡単に求めることができます。

例えば、グループAは成功した人が160人で失敗が40人、一方、グループBは成功が120人で失敗が80人だったとします。成功率はグループAが80%、グループBが60%となりますが、これだけでは統計的に有意差があるかどうかまではわかりません。
R言語を使えば簡単にp値を求めることができます。この例であればp値は5%より小さいので、統計的な有意差があるとみなせます。
R言語であれば、160、120、40、80という4つの数字を関数に入力するだけでp値を計算することができます。
ExcelにもCHISQ.TEST関数があり、カイ二乗検定を行うことができます。しかし、R言語とは違って、160、120、40、80という4つの数字を関数に入力するだけでは計算できず、少し事前準備が必要となります。

結果はRと同じになる。
具体的には、実測値をもとにして期待値を計算する必要があります。上記の例であれば、グループAで成功する人の期待値は、200 × 280 ÷ (280 + 120) = 140 となり140人です。これを他の組み合わせについても計算します。
そして、CHISQ.TEST関数に実測値と期待値の2つを入力することでp値が計算されます。もちろん、R言語と同じ値になります。
このようにExcelを使ってもカイ二乗検定を行うことができますが、期待値の表を事前に作るというステップが必要になります。
統計学と経営のセンス
定量的なデータを分析する際に統計学的手法を使うことがあるとお伝えしました。
二つの集団の平均値に差があるかどうかを調べるときによく使われる手法としてt検定があります。Excelにも関数や分析ツールとして提供されており、
手軽に使うことができます。
このt検定では、グループAとグループBの平均値が統計学的に見て差がある(有意差がある)かどうかを調べることができます。
具体的には、統計学的に見て、AとBの平均値の差が滅多に起こらないのであれば、有意差がある、と判断します。滅多に、という部分はなかなか難しいのですが、一般的には5%未満とか1%未満の確率でしか起きない、という判断になります。1%未満でしか起きない差なので、差がある、ということですね。
ビジネスの現場であれば、このような使い方です。対象とする顧客グループAとBで購買金額の平均に差が見られた。t検定で調べると、この差は1%未満でしか起きない差なので、確かに差がある(有意差がある)、という使い方ですね。
悩ましいのは、平均に差はあるが、統計学的には差がみられなかったケースです。例えば、Aの平均が一人2000円で、Bの平均が1000円であった。しかし、統計学的には有意差はなかった、という場合です。
2倍の差があるので、一般的には狙うべき顧客グループとしてはAになりますが、本当に差があるかどうかはわからない状況です。予算的にAとBの両方を追いかけることが難しい状況であれば、Aを狙うのか、あるいは、別のセグメントを探すのかは、まさに経営センスによる判断をすることになると思います。
もしかするとサンプル数が増えてくるとAとBに統計的な差がでるかもしれませんし、逆に、今見えている平均の差がなくなってしまうかもしれません。
どちらになるのかは誰にもわからないでしょう。そのようなわからない状況でも判断しなければならないのは勇気がいることですし、経営の醍醐味とも言えるかもしれませんね。
反対に統計学的に差があるが、平均には大きな差がないケースもありえます。Aの平均が1010円で、Bは1000円といったケースです。顧客数が非常に大きく、この10円の差が経営上大きな差を生むのであればAを狙うのは意味がでてきます。しかし、そこまで顧客数がなければ、10円の差は他で吸収できる差と見なして、他のセグメントを探す、という判断もでてきますね。
