
アンダーソン局在
量子力学の教科書で勉強していると、重要だが単純なポテンシャルに関する内容が多い。もちろん現実の系は複雑であるから、単純な系からは想像も付かない多彩な世界が広がっている。その典型的な例としてアンダーソン局在を考えてみる。これはランダムな媒質中の電子が局在し、特に電気伝導を示さないという現象である。複雑な量子系で初めて発生する現象であり、1958年にP. W. Andersonによって見いだされた物理学史上極めて有名な発見の一つである。低エネルギーの状態では局在がおこり、エネルギーが高くなると非局在化(つまり電気伝導が可能)するということで、金属・絶縁体間転移などの観点から膨大な研究が行われた。
といった一通りの解説を目にしてもすぐにイメージが湧く人も少ないのではないだろうか?そこで専門的な文献では省略されているような初歩的な疑問を解消するべくシュレーディンガー方程式の数値計算をした。やってみると意外に面白く、こちらでもシェアさせて頂きます。
ポテンシャルの形
以下のようなランダムな振る舞いをするポテンシャル中の2次元井戸型ポテンシャルを考えた。格子のサイズは縦横100✕100の合計10000点である。格子上に与えたポテンシャルの値は0から2を取り、この領域外には電子がしみ出さないとした。同様の系はこの論文(Filoche and Mayboroda, 2012)でも考察されている。

以下の数値計算にはMathematicaを利用した。Mathematicaに搭載されている複数の数値計算アルゴリズムを可能な限り試して結果が一致するのを確認している。
局在状態
エネルギーが低い領域では局在が発生する。以下の図は波動関数の二乗、つまり電子の分布密度を表示している。これは第一励起状態(基底状態の次、エネルギー0.747)である。青い部分は電子が存在しない領域である。

非局在状態
エネルギーが高くなるに従って電子は様々な場所に存在するようになる。以下の図は603番目の励起状態で、エネルギーは2.030、つまりポテンシャル上端より少しだけ高いエネルギーを持つ状態である。

もっと沢山の図
紙の教科書と違って大きな図を入れられるので、エネルギーの変化によってどのような振る舞いを示すのかを調べてみよう。基底状態から始まる各励起状態を1,2,3...と番号付けする。まずはそれらのエネルギー分布を示す。

基底状態から始めて、1,2,3,...12番目の状態は以下の通り(左から右、上から下の順)。この辺りでは強い局在が見られる。各励起状態ごとに局在する場所が移動するのがおもしろい。

次は1,11,21,31...,121番目(つまり10個おき)の状態を見てみよう。これはポテンシャルのちょうど中腹辺りに存在する状態である。

最後に1,51,101,151,...,601(つまり50個おき)の状態を見てみよう。最後の方はポテンシャルの上端より少し上くらいのエネルギーを持っている。

参考までに、1000番目の状態(エネルギー3.340)は次のようになる。

規則系から不規則系への遷移
規則的な格子に徐々に不規則性を印加していって徐々に局在が発生する様子を観察するのも興味深い。以下は整数座標(i,j)に1+(-1)^(i+j)を並べた格子状の規則的なポテンシャル。

この系では格子の存在に関わらず大域的に分布する波動関数が得られる。以下は基底状態から始めて1,2,...,12番目の状態を順に表示している。

この規則的な格子に、各点で最大0.4のランダムなポテンシャルを重ねると以下のようなポテンシャルとなる。
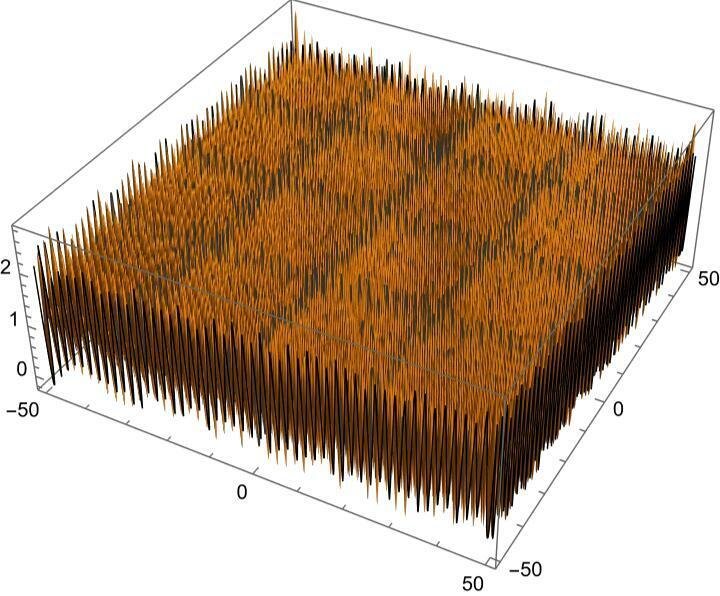
この場合も1,2,...,12番目の状態を表示すると、以下のように弱い局在が発生することが観察できる。

