
ちょい調べた!拡散モデルとは?【学習編】
前の記事「ちょい調べた!拡散モデルとは?」では、拡散モデルの原理を解説しました。本記事では、拡散モデルの学習について解説します。

ちょっと復習しておきましょう
拡散モデルは、「拡散過程」と「デノイズ過程」の2つのプロセスがあります。
拡散過程では、観測データに対して、Gaussianノイズ(正規分布に従うもの)を足していきながらデータを完全ノイズにしていく処理を行います。

デノイズ過程では、ノイズを加えられたデータから元のデータへ復元する、ノイズ除去を行います。

拡散モデル学習
拡散モデルの学習は、対数尤度の最大化で行われます。対数尤度の最大化による学習というは、「あるデータが得られたとき、そのデータを最も観測しやすい(尤もらしい)モデルのパラメータを探す方法」のことです。拡散モデルでは、パラメータとなるのは、デノイズ過程で使われるニューラルネットワークのパラメータです。しかしながら、拡散モデルの対数尤度の計算は困難であるため、その下限であるELBO(Evidence Lower BOund)を使って最大化することが一般的です。
ELBOの導出
まず、拡散モデルの対数尤度からELBOを導出してみましょう。

このように、対数尤度の下限ELBOは以下のように表される。

次に、ELBOを展開してみます。

最大化する目的関数の近似
ニューラルネットワークのパラメータ(\theta)について最大化していきたいので、ここで、そのパラメータを含まない項については、最適化の過程で無視できます。そうすると、我々が最大化すべき目的関数は以下のJ(\theta)となります。

この目的関数から注意してほしいのは、各計算で使われるサンプルは、拡散過程における元のデータ(x_0)から時刻t-1のサンプルと、時刻t-1のサンプルから時刻tのサンプルの二つだけということです。しかしながら、Tの値が大きいので、その計算量はまだ大きいということは想像できます。そこで、この目的関数の近似を行います。ここで使われるのは、T個の変数の和を、一様分布の期待値と近似することです。そして、その近似された期待値はモンテカルロ法によってさらに近似することができます。つまり、目的関数を以下のように近似されます。

そして、デノイズ過程のモデル化を使ってさらに目的関数を展開すると、以下のように近似できます。

今までの近似処理をまとめると、以下の手順で目的関数が計算されます。

さらにELBOを近似する:
一回のサンプリンで目的関数を計算する
今までの計算では、各学習データにおいて、2回サンプリングをしなければなりませんでした。そこで、そのサンプリング回数をさらに減らして、1回のサンプリンでできるように、目的関数をさらに近似することを考えていきます。

まず、上記の目的関数の途中の近似から出発点として考えます。我々の目的は、その目的関数が最大となるようなパラメータを探すことです。これを式で以下のように表されます。

KLダイバージェンスは、2つの確率分布が等しい時に最小値(0)となりますが、ここのJ'はマイナスダイバージェンスのため、ここでの目標である最大値を取るのは、以下の分布が一致する時です。

ここまでの導出をまとめると、目的関数は以下のように表されます。

ここで、目的関数に -1/T倍し、損失関数Lを定義することで、ELBOの最大化はその損失関数の最小化と等価します。また、モンテカルロ法により以下のように損失関数を具体的に計算できます。
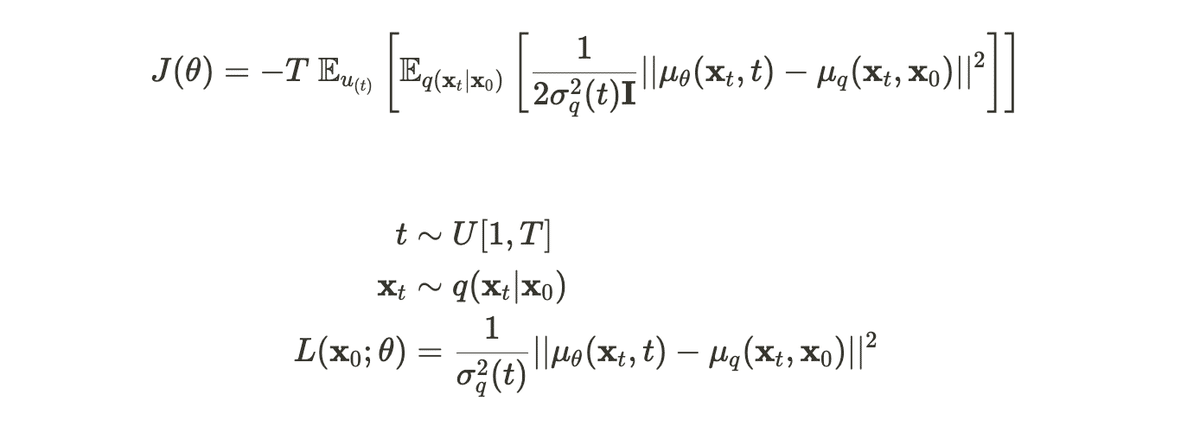
この損失関数から分かるように、今回の学習では、ニューラルネットワークの出力が拡散過程でのq(x_{t-1}|x_t, x_0)の平均ベクトルに近づくようにパラメータを調整することをやっています。以上をまとめると、拡散モデルの学習アルゴリズムは以下のように表されます。

より効果的な学習:元データの復元ORノイズ予測
ここまで、デノイズ過程のニューラルネットワークが予測するのは、元のデータと拡散過程により完全ノイズ化されたデータとの間の「内分点」を教師データとしたものです。それは上記の学習アルゴリズムのステップ5からわかります。つまり、ノイズのデータから少しノイズ除去されたデータへの処理が行われるネットワークが学習されています。
上記のことをもっと考えてみると、少しだけノイズ除去されたものを予測するのではなく、元のデータを復元するようにニューラルネットワークを学習させることも考えられます。さらに、元画像ではなく、そのもの画像に足されたノイズを予測することも考えられます。それらの方法を実現する、拡散モデルの学習アルゴリズムは以下のように改修することで実現されます。



次の記事では、今回見てきた学習方法を実装し、実際の画像データの生成モデルを構築してみます!
参考文献
オライリー・ジャパン出版の「ゼロから作るDeep Learning ❺ 生成モデル編」
