
AlphaGeometryの技術を読み解く〜生成AIが数学オリンピックに挑戦
生成AIが苦手とされる数学に、Google DeepMindが挑戦しました。国際数学オリンピックの幾何学 (Geometry) の難問を解き、金メダリストに肉薄する結果です。生成AIが、次の段階に進化するブレークスルーかもしれません。
そんなAI「AlphaGeometry」について、技術ブログとNature論文があります。そこで、小学校の算数ができる人なら、誰でも理解できるように、読み解いてみます。
国際数学オリンピックで金メダルに迫る
国際数学オリンピック (IMO: International Mathematical Olympiad) は、高校生などを対象とした数学の競技です。各国で選抜された数学の天才たちが、世界中から参加します。参加者の上位層に、金・銀・銅メダルが授与されます。
🥇金メダル:上位 1/12 (8%)
🥈銀メダル:上位 2/12 (17%)
🥉銅メダル:上位 3/12 (25%)
2000年から2022 年までのオリンピックから編集された 30 の幾何学問題 (IMO-AG-30) において、AlphaGeometry は競技時間制限内で 25問を解きました。これは、銀メダリストを上回り、金メダリストに肉薄する結果です。

従来の最先端 (State of the Art) のAIでは、10問しか解けておらず、AIの大きな飛躍と言えます。
小学校の算数を思い出す
数学オリンピックの難問を見ても、我々のような一般人には理解が難しいです。そこで、数学の幾何学の基礎となる、小学校の算数の図形問題を思い出します。
二等辺三角形として、AB = ACの三角形を考えます。このとき、角B ($${ \angle ABC }$$) と 角C ($${ \angle BCA }$$) は等しいはずで、それを証明しましょう。
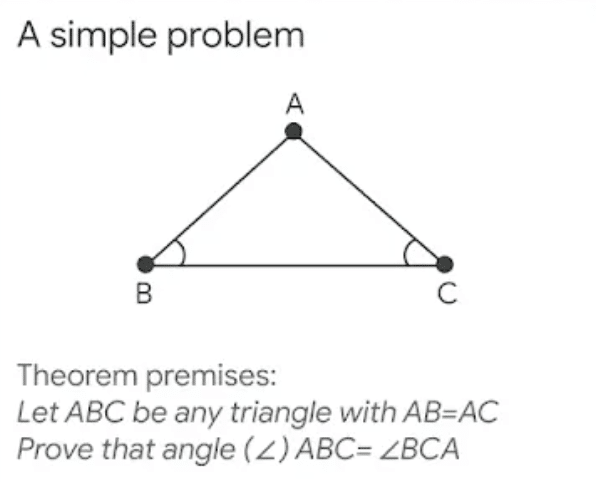
こういった図形問題を解くのに役立つのが「補助線」です。ここでは、頂点Aから、底辺BCの中央Dに、線ADを引いてみます。
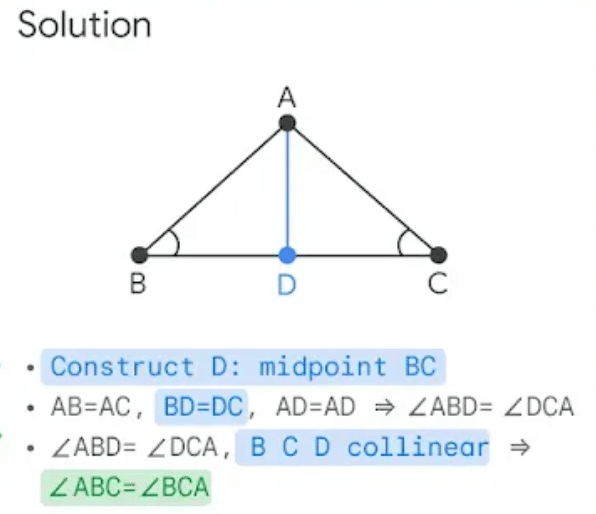
そうすると、以下のように丁寧に推論できます。
・点D を 線BCの中央に置く
・$${AB=AC}$$、$${BD=DC}$$、$${AD=AD}$$なので、(三角形ABDと三角形ACDは同じであり)、 $${ \angle ABD = \angle DCA}$$
・$${ \angle ABD = \angle DCA}$$であり、BとCとDは直線上にあるので、$${ \angle ABC = \angle BCA}$$ と証明できる
ここには、2つの思考があります。
直観(速い思考):線ADの補助線を思いつく
熟考(遅い思考):図の形や距離などをもとに、論理的に推論する
AlphaGeometryの仕組み
言語モデルと記号計算エンジンのコラボ
AlphaGeometryは、先ほどの2つの思考を、2つのモジュールで実現します。
直観(速い思考):言語モデル (Language model)
熟考(遅い思考):記号計算エンジン (Symbolic engine)
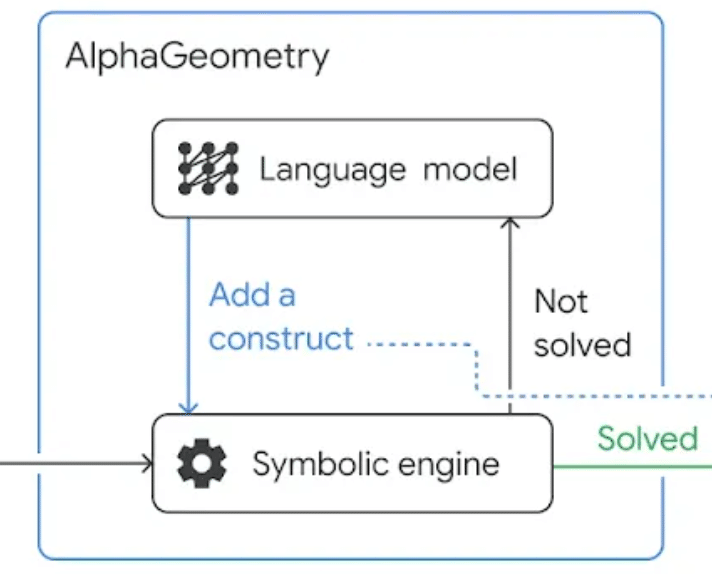
AlphaGeometryは、問題(定理の前提)が与えらると、記号計算エンジンが解を探します。解が見つからない場合は、言語モデルが新しい要素を追加し (青) 、記号計算エンジンが解を探します。解が見つかるまで、言語モデルと記号計算エンジンのループが続きます。

ちなみに、歴代の数学オリンピックで難しいとされる2015年の問題では、AlphaGeometryの回答が109論理ステップに及んだそうです。

言語モデル〜直観で補助する
言語モデルには、大量の学習データが必要です。しかし、高度な幾何学の問題と回答のセットは、大量にはありません。そこで、学習データをAIで大量に生成しました。
まず、10億個の図形をランダムに生成します。
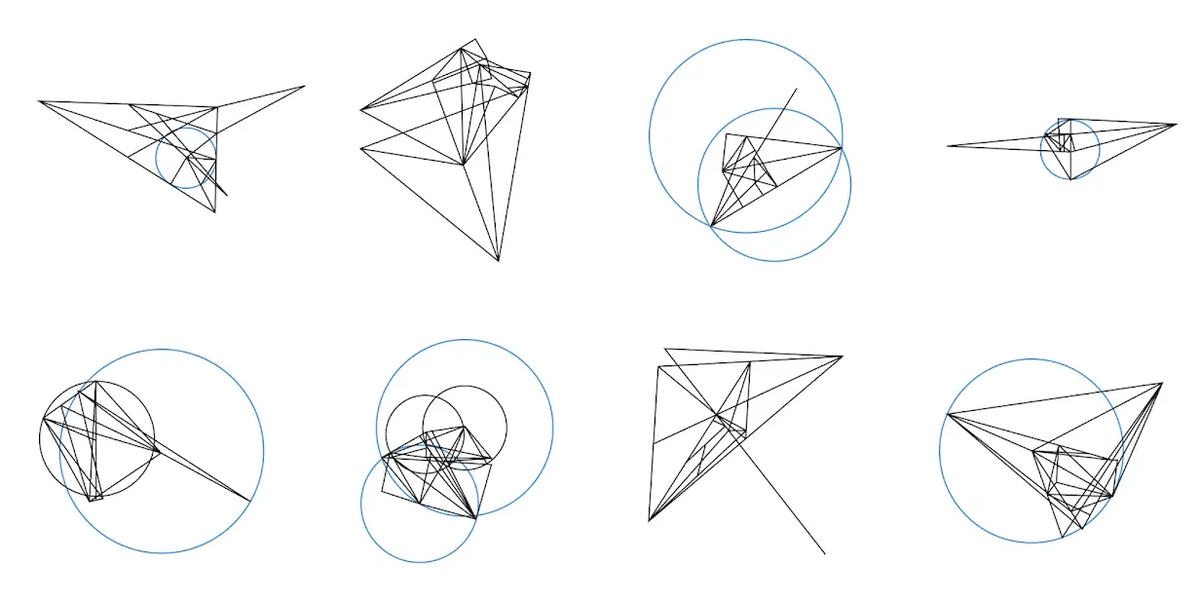
次に、記号計算エンジンで、各図に含まれるすべての証明を見つけてから、それらの証明に到達するために必要な追加構成があれば、それを逆算して見つけ出します(記号演算とトレースバック)。

そして、そこから問題と証明を作り出します。全体の流れは、図aの前提から、図cの問題と証明を作り出すイメージです。
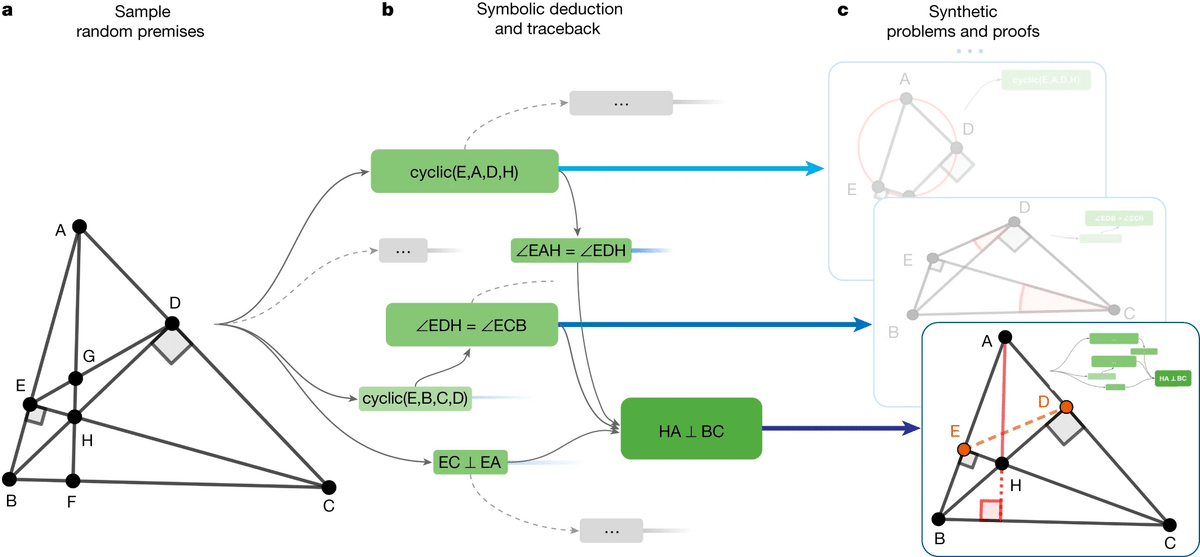
そして、内容の重複を除いた結果、1億のデータセットが得られました。それをもとに、大規模言語モデルでも利用されているTransformerをトレーニングしています。
事前学習:1億のデータセット。「<前提> <結論> <証明>」という構造を持つシリアル化されたテキスト文字列。
ファインチューニング:900万のデータセット。1億の内、補助構造が含まれる9%を利用して、補助線を引くことに強化。
パラメーター数:1.51億(大規模言語モデルは100億レベルなのに比べて小さい)
トークン数:1,024
記号計算エンジン〜熟慮で計算する
記号計算エンジンでは、2種類のエンジンで構成されています。
DD (Deduction) : 「A, B, Cが同一線上にある」のような幾何学的な計算
AR (Algebraic Rules) : 「距離AC = 距離AB + 距離BC」のような代数規則による計算

記号計算エンジンとして、DDとARを高度に統合した点が、この研究の特徴です。
AlphaGeometryの評価
2000年から2022 年までのオリンピックから編集された 30 の幾何学問題 (IMO-AG-30)を、精度評価のためのベンチマークに利用します。従来の最先端のAI、GPT-4などとの比較結果を抜粋します。
$$
\begin{array}{|l|c|c|} \hline
手法 & 正解数(30問中) & 正解率 \\ \hline
従来の最先端 & 10 & 33\% \\ \hline
\text{GPT-4} & 0 & 0\% \\ \hline
DD + AR & 14 & 47\% \\ \hline
DD + AR + \text{GPT-4} & 15 & 50\% \\ \hline
DD + AR + 人間 & 18 & 60\% \\ \hline
\text{AlphaGeometry} & 25 & 83\% \\ \hline
\end{array}
$$
ここから言えることは
GPT-4単体では、数学オリンピックの問題を全く解けない
記号計算エンジン (DD+AR) が、従来の最先端AIを超えている
記号計算エンジン (DD+AR)にGPT-4を組み合わせても、成績はあまり伸びない
記号計算エンジン (DD+AR)に特化した言語モデルを組み合わせると (= AlphaGeometry) 、成績が著しく伸びる
もう少し踏み込んで言えることは
汎用的な大規模言語モデルより、特化した小さな言語モデルと推論エンジンの組み合わせの方が、高い性能になることもある
ただ、国際数学オリンピックの30問だけだと少ないので、教科書の例や演習、地域オリンピック、有名な幾何学の定理などを加えた、231問でも評価しています。簡単な問題が増えるので、全体的な正解率は上がりますが、AlphaGeometryの正解率の高さが際立っています。
$$
\begin{array}{|l|c|c|} \hline
手法 & 正解数(231問中) & 正解率 \\ \hline
従来の最先端 & 173 & 75\% \\ \hline
DD + AR & 198 & 86\% \\ \hline
DD + AR + 人間 & 213 & 92\% \\ \hline
\text{AlphaGeometry} & 228 & 99\% \\ \hline
\end{array}
$$
AlphaGeometryの応用
AlphaGeometryは、数学の中でも幾何学に特化して、開発・評価されました。しかし、この言語モデルの本質的な能力は、問題を解くための「補助 (Auxiliary)」を生成できることにあります。そして、補助が問題解決のカギになるケースは、幾何学だけではありません。例として、4つ挙げられています。
数論 (Number Theory)
方程式 (Solving Equation)
組み合わせ論 (Combinatorics)
不等号 (Inequality)
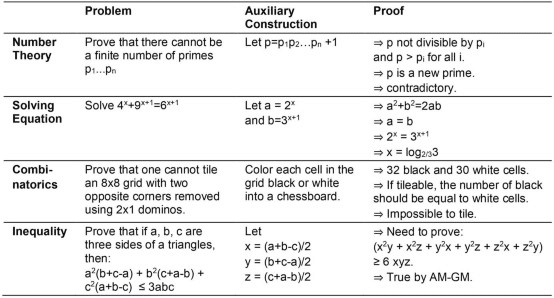
このように、生成AIが数学の能力を獲得したことで、さらにAIが進化することを期待しましょう。
いいなと思ったら応援しよう!

