
【点数計算の処方せん】「ロンは言えるけど、ツモが言えないよ~(๑-﹏-๑) 」の民へ
今回の記事は、ある程度点数計算をマスターしているもののなかなか実戦では完璧に出来ないという方。
具体的には、1300 や 7700 など「ロン」の点数はすぐ言えるけど、400・700 や 2600オール など「ツモ」の点数がなかなか出てこない、という方を想定して書きました。
ですが、少しでも多くの方に役立てていただける内容を心がけましたので、点数計算の苦手な方は興味のあるところだけでも読んでいただけると幸いです。
■ロンはすぐ言えるけど、ツモがなかなか言えない
というそこのあなた!安心してください。
複雑な点数計算早見表を丸暗記しなくても “100%確実に” 言えるようになる方法があります!
それがこちら!ドンッ!
① 子:100の位が奇数なら100点を足す
② 親:3で割れるように100点か200点を足す
たったこれだけです!例外は一つもありません。
これだけではよく分かりませんね。説明します。
■コツ① 子:100の位が奇数なら100点を足す
子でツモ和了りした場合、和了り点の「1/2を親」から「1/4を子」からもらうので、基本的には「半分、さらに半分」としていけば大丈夫です。
2000のツモ和了りなら、
半分の1000を親に、さらに半分の500を子に
という具合ですね。
ですが、2000のように割り切れる場合は簡単ですが、ハンパなときが困ってしまいますよね?
安心してください!
100点を足す
たったこれだけで解決です!これで100%対応できます!

例えばこちら。
子の40符1ハンなので、ロンなら1300点ですがツモだとどうでしょう?
1300 を半分にすると 650 でハンパになってしまいますよね?
単純に10の位を繰り上げて 700 と考えても全く問題ありませんが、最初から 1300 に 100 を足して 1400 にしてしまう方がシンプルで良いかな、と思います。
はい、実際にやってみましょう!
1300
→ ハンパになるので100を足す
→ 1400
→ 半分の700を親から
→ 700がまたハンパなので100を足す
→ 800
→ 半分の400ずつを子2人から
こんな感じです。
この方法を使えば、複雑な点数計算早見表の丸暗記は必要ありませんし、この方法には例外が一つもありません。
■コツ② 親:3で割れるように100点か200点を足す
親は子に比べるとほんの少しだけ難しいです。
理由は簡単。2の割り算より3の割り算の方が難しいからですね。
でも安心してください!
必殺技を伝授します!
■必殺技:各ケタを足して3の倍数なら3で割れる
たったこれだけです。
有名なので知っている方も多いと思いますが、知らない方にとっては点数計算の大きな武器になるのでぜひ覚えていただきたいと思います。
詳しく説明します。
例えば、14672。
この数字、パッと見で3で割れるかどうかはわからないですよね?
そういうときは各ケタを足してみます。
1+4+6+7+2=20
20 は 3 の倍数ではないので、14672 は 3 で割れない
ということになります。
では、14672 に 1 を足して 14673 にしてみましょう。
各ケタの合計は 20+1 なので 21 ですね。
21 は 3 の倍数なので、14673 は 3 で割れる。
こんな具合です。
さてさて。
和了り点を3で割れるように100点か200点を足す
これが親のときのコツでしたね。

親でこんな手を和了ったとします。親の40符3ハンですね。
さて、何点オールになるでしょう?
これも実際にやってみましょう!
親の40符3ハンのロン和了りは 7700
→ 7700 の各ケタを足すと 7+7+0+0=14
→ 14 は 3 で割れないので、7700 も 3 で割れない
→ 7700 に100 を足して 7800 にしてみる
→ 7+8+0+0=15
→ 15 は 3 で割れるので 7800 も 3 で割れる!
はい。これで、7800÷3 の答が子一人からもらう点数、ということが確定しましたね。
ですが……
はい!7800÷3=2600 なので 2600オール です!めでたしめでたし!
……とはならないんですよね。
もちろん 2600オール で合っていますよ。合ってますが…
この計算が瞬時にできる人は、既に点数計算をマスターしているはずなんですよね…
はい!ここで、計算が苦手な方に朗報です。
■点数計算に計算はほぼ不要
これ本当です。
さすがに全く不要というわけではありませんが、ほぼ必要ないと言っても過言ではありません。
では、何が必要かと言えば 暗記 なんですね。
「いやいや、あなた表を丸暗記する必要ないって言ったでしょ!」
というツッコミがあちこちから聞こえてきそうです。
もちろんそれはそうです。
あんな複雑怪奇な点数計算早見表を丸々暗記する必要は全くありません。
ただし、本当に最頻出の20~50符だけはさすがに丸暗記してしまった方が良いです。
なぜなら、20~50符が最頻出ということに加え、全ての符が20~50符の応用に過ぎないからです。
例えば、
・60符2ハン は 30符3ハン
・80符2ハン は 40符3ハン
・90符2ハン は 30符2ハン × 3
というような関係性になっているので、20~50符 さえ覚えてしまえば全ての符に応用が利きます。
一応、20~50符と言いましたが、50符は20~40符よりは出現頻度が低いのと、5(50)は 2・3・4(20・30・40) で割れないために点数の被りがないので、50符だけを独立して覚える必要があるんですね。
ですので、50符だけ後回しにして、まずは 20~40符 だけ丸暗記してしまう、でも全然大丈夫です!
ということで、シンプルな表を用意しました。ドンッ!

巷にある点数計算早見表って細かすぎて覚える気がしなくないですか?
なのでシンプルにしました。
とりあえず、これだけ覚えてしまいましょう。
画像を見ていだだくと一目瞭然ですが、緑・黄色・赤の同じ色のラインは親子関係なく点数が完全に被っているんですね。
これは逆に言えば、
20~40符の場合、どこかで出てくる点数はほぼ他のどこかでも出てくる
ということです。これ、ものすごく大切なポイントです。
このように、20~40符は被りがとても多いので、点数の入る箇所は全54箇所(満貫を除く)もありますが、覚える点数の種類はたった15種類しかありません。
話を戻しましょう。
親の40符3ハンのロン和了りが7700点(100点足して7800点)なのはわかるけど、2600オールがすぐに出てこない問題
でしたね。
これに関しては、最終的には暗記というか慣れで、脳死でも 2600オール と言えるのが目標ではあるのですが、ここでは「早見表に頼らずに言えるようになる方法」を探っていこうと思います。
20~40符の場合、どこかで出てくる点数はほぼ他のどこかでも出てくる
ということを先述しましたが、これが本当に本当に大切なポイントなんですね。
計算があまり得意でなくても、
7800÷3 の答が 二千ホニャララ
というのは何とかわかりますよね?
そしてさらに、
20~40符は親子またいで被りが多く、それゆえ
どこかで出てくる点数はほぼ他のどこかでも出てくる
という重要ポイントがありましたよね。
それらを踏まえてこの画像をご覧ください。ドンッ!

赤い太字に注目してください。なんと!
20~40符で「二千ホニャララ」って 2600 と 2900 しかないんです!
2900に3を掛けると9000よりちょっと少ない、というのは何となくわかりますよね?
さらに、2600 の百の位である 6 に 3 を掛けると 18、つまり百の位が 8 になるので 7800 に矛盾しませんね。
なので、7800 は 2600オールと確定できるというわけです。
文字で書くとだいぶ面倒くさく見えてしまいますが、
実戦中に 7800÷3=2600 の計算をしているのではなく、単に暗記というか直感的に「2600オール」と言っているだけ
ということを理解していただければと思います。
点数計算が早い人って結局、これの延長線上にいるだけのことなんですね。要は慣れです。
とは言え、まだまだ不安な方がたくさんいると思うので、ちょっとしたコツやマインドをいくつか挙げてみます。
■語呂で覚える
これは昔ながらの方法ですね。
リアマ出身だとこれで覚えた方が多いと思いますが、ネトマ派の方にもとても有効な方法だと思います。
有名なところを表に書き込んでみました。
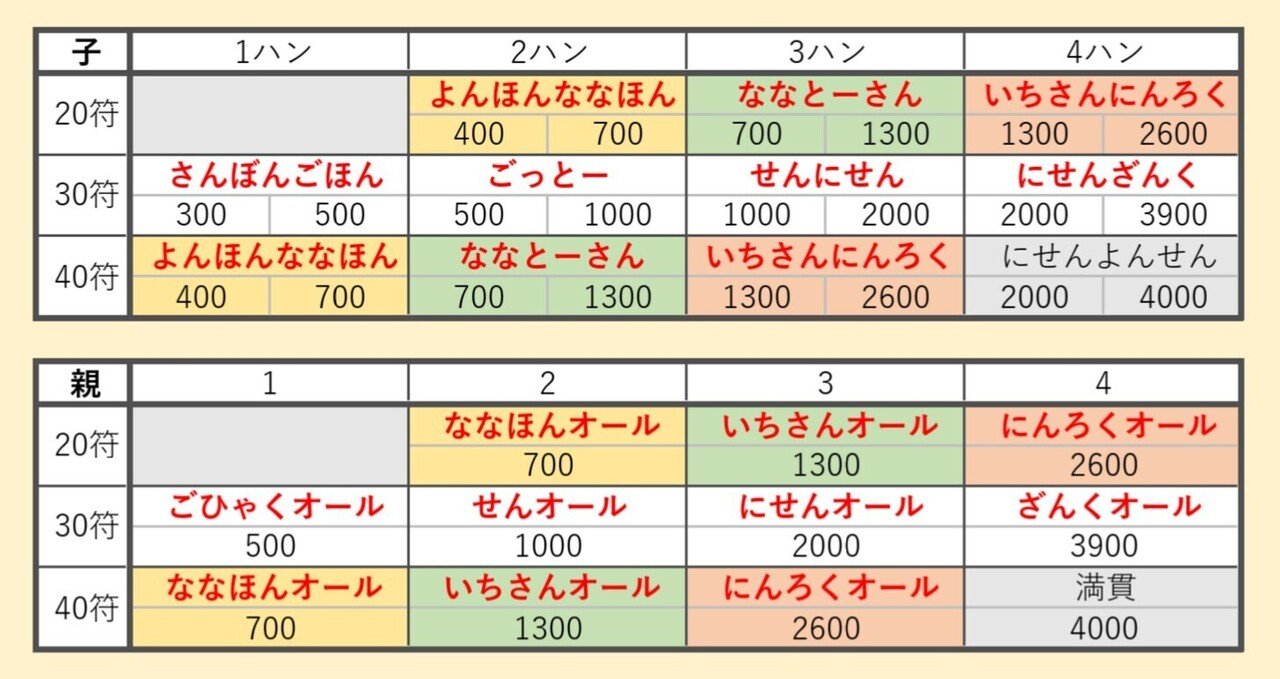
赤い太字が語呂合わせです。どうでしょう?
700・1300 といった無機質な数字の羅列より「ななとーさん」の方がだいぶ覚えやすくありませんか?
そして、黄色・緑・赤の同色部分は完全に被っているので、子ならたった7つの語呂を覚えるだけです。
どうでしょうか?気合いを入れれば1時間くらいで覚えられそうな気がしませんか?
一応、ネトマ専門の方に説明しておきますと、「さんぼんごほん」は「3本5本」、「ななほんオール」は「7本オール」、つまり百点棒の本数を表しているんですね。
また、親は点数に「オール」を付けただけなので、わざわざ語呂を覚える必要はありません。
一応、親も参考に載せましたが、語呂は子だけ覚えれば十分でしょう。
■“白地図” ならぬ “白早見表” で訓練する
移動中などの細切れ時間で勉強する場合は大体スマホを活用することになるので、スマホでも効率的に学習できるようExcel (スプレッドシート) などに “白地図” ならぬ “白早見表” を作成し、パズル感覚でポチポチと穴埋め作業をしてみるのもお勧めです。

Excel (スプレッドシート) で表を作成するのがめんどうでしたらメモ帳などで充分です。
要は、インプットとアウトプットの両方をバランスよくトレーニングするのが大切ということですね。
実戦で必要なのはアウトプットなので、インプットだけではなかなかマスターできませんよ!
■点数計算には明確なゴールがある!
麻雀が強くなるための技術やメンタルの向上にはゴールがありませんよね。
ですが、点数計算には明確なゴールが存在しています。
そして、それは点数計算の苦手な方が想像しているよりは恐らくだいぶ近くにあります。
ブレイクスルーというやつでしょうかね。
ある日突然、「今までなんで出来なかったんだろう?」と思う日が来ます。
ゴールがあることを知っているのと知らないのとでは、取り組む上での辛さがだいぶ変わってきますので、このことはしっかりと心に留めておいていただきたいと思います。
ここで言う「明確なゴール」とは、
・点数が自分の力でわかる
・点数計算で損をしない
・点数計算で他人に迷惑をかけない
ということです。
■仲間に達成度をチョイチョイ教えてもらう
点数計算には明確なゴールがあり、それは点数計算の苦手な方が想像しているよりは恐らくだいぶ近くにある
ということを先に述べましたが、そうは言っても点数計算で悪戦苦闘している方にとっては、なかなかゴールがイメージしづらいのではないかと思います。
なかなか先が見えないとつい挫けてしまいそうになりますが、そんなときは仲間に
「自分が今、点数計算を何%くらいマスター出来ているか」
を聞いてみてください。
自分のイメージが50~60%くらいだとしても、仲間から見ると80~90%くらいだというケースも少なくないと思います。
それくらい、多くの方が「あともう一歩」のところで足踏みしてしまっている、ということなんですね。
点数計算マスターを10合目に例えると、8~9合目あたりに大きな障害物があるようなイメージです。
道のりとしては80~90%くらいのところまで来ているのだけど、最後にもう一踏ん張り、ラストスパートをする必要がある、ということなんですね。
80%を越えたあたりからなかなか先に進まなくなりますが、
80% → 81 → 82 → 83 → 84 → 85 → 100%!
みたいな感じで、その時はいきなり訪れる場合が多いです。
きっとあなたも、あともう一歩です!頑張ってくださいね!
この記事が気に入ったらサポートをしてみませんか?
