【SEでも機械学習】私がつまづいた勾配降下法
勾配降下法は機械学習の肝だな~、と思いつつも、その仕組みが初学者には難しいんですよね。。
私の数学知識は高校レベルの微分と線形代数なので、難しい数式で説明されても分からないが、簡単なお絵描きだとイメージしかつかめない、、と言う状況。ちょうど良い資料がなかなか見つからないんですね。。
いろいろ探して一番しっくりきたのが以下の書籍。
お絵描きと数式と実装コードが記載されているので、順に読んでいくだけで「機械学習の内部ってこうなってるのか」とイメージできるようになってます。。が、
それでも私には難しかった。。
で、最終的には数学的な正確性度外視で本記事のように理解してます。
上記書籍のお絵描き/数式/実装コードの行間を、自分なりの埋めてみたという資料なので、私と同レベルの初学者の方には参考になるかもしれません。
まず以下は前提知識(超ざっくり版)です。
勾配降下法って何してる子?
初学者は、コスト関数(例:誤差平方和)を最小化する(0に近づける)仕組み、という理解で良いと思います。数学的正確性や、正しい言葉使いを考えるとこんがらがると思うのまずはざっくりで。
じゃ、コスト関数って?
ラベルと言われる答え(y)と、答え(y)を導くために作った関数f(x)の誤差を計算する数式。すごく簡単に考えると、 y - f(x) ですよね。
記事内で上げている誤差平方和も y - f(x) がベースですが、誤差を2乗してます。
この辺りで??となる方は、最小二乗法等を復習されると良いかと、、私も復習しましたが、ググれば数学の教科書より分かりやすい良質資料が山ほどあります。
コスト関数を最小化するとは?
ここで微分(偏微分)が出てきます。。が、
コスト関数の微分方法なんて分からなくても、イメージだけなら高校で学んだ微分の延長です。コスト関数が微分できたとしたら、その傾き(勾配)0が極値になるなぁ~、、という感覚で十分かと。
ただ極値は最小値ではないので、「局所的最小値につかまる」というようなこともありますが、ここでは割愛します。
【閑話】
これ以降で数式が出てきます。数式が理解できれば簡単な話ですが、、初めはちんぷんかんぷんだと思います。私はそうでした。。
なのでごちゃごちゃ書いている式で結局何がしたいのか?を先にお話しすると、「最適な"w"を求めたい」と思ってください。
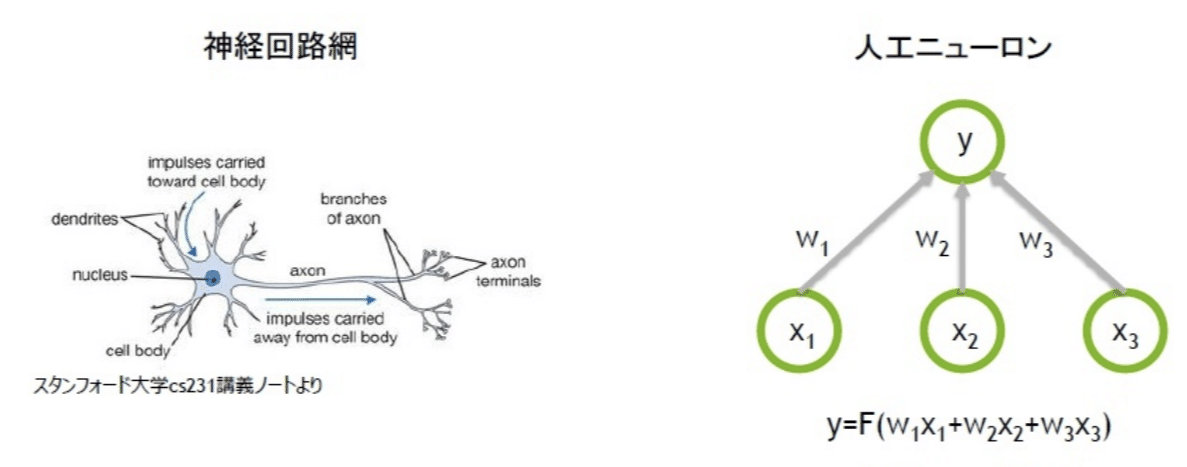
"w"ってなんだ?と思った方は、一番上のお絵描きの「人口ニューロン」を参照ください。そこに記載している"w"とイコールで、f(x)の関数の中で使われる値(高校数学ではa、bで表していたのも)です。
最適な"w"が出てくると何が嬉しいかと言うと、
誤差が0に近づくよね ⇒ 結果、関数f(x) ≒ (y)になるよね ⇒ xに未知の値を代入数ることで予想ができるよね、、と言う感じです。(計算上は逆になる部分があるのでイメージとしてとらえてください)
【休題】
お絵描き/数式/実装コードの行間補足
以下はコスト関数の y や x に分析データがどう代入されるかを図解したものです。ここでは分析データの行と列がどのように計算されるか?がイメージできれば良いかと。

以下はよくある勾配降下法のイメージ図と数式をリンクさせたものです。
私のように微分から学び直ししていると、、この辺もごちゃごちゃになってしまうので、簡単な補足資料です。

以下は"w"の更新式になります。
前提知識でもお話した通り、結局何がしたいか?と言うと「適切な”w”を見つけたい」ので、ここが一番のポイントになります。
(ここで言う"w"の更新は、上の図の勾配を0に近づけることと同義)

以下は計算フローの中で"w"の更新がどう行われているか?の簡易図です。
①初回はランダム生成した"w"を使ってf(x)を作り、1エポック目の計算を実施
②誤差関数により y との誤差が分かるので、更新式によりη分だけ誤差を修正した新”w”を算出
③新"w"を適応したf(x)で2エポック目の計算を実施
以降は上記をエポック分繰り返えすことで、f(x)の正しさ具合を上げていく流れになります。

最後に上で紹介した書籍に掲載されている実装コード(Git公開されているもの)と、これまで数式をつなげてみました。
自分でいうのもなんですが、、分かりづらいですね。。まぁご参考まで。
https://github.com/rasbt/python-machine-learning-book-3rd-edition

以上になります。
数学的な正確性は度外視ですが、私と同レベルの初学者の方のお役に立てれば幸いです。
この記事が気に入ったらサポートをしてみませんか?
