
Tsesseract 4次元・超立方体ふたたび(2)
(1)からの続きです。
さて、前回はTesseractもどき立体、というボードゲーム案を考えました。
でもこれ、もどき、であってニセモノです。
じゃあ、ホンモノのTesseractでは「直線状に並ぶ関係になってる立方体」が本当は何組あるのでしょう?そして、各々の直線どうしは、どんな空間配置(位置関係)なのでしょうか。
*この後に続くのは、純粋数学(幾何学)の話です。ボドゲに応用するのはたぶん無理だろうという話が続きます。ご注意ください。
このページトップに示すTesseractモデル図をもとに説明すると「白緑黒赤」の4つの「立方体」は「直線状に並ぶ仲間」です。ずっと左に無限にまっすぐつながっているし、ずっと右に無限にまっすぐつながっています。
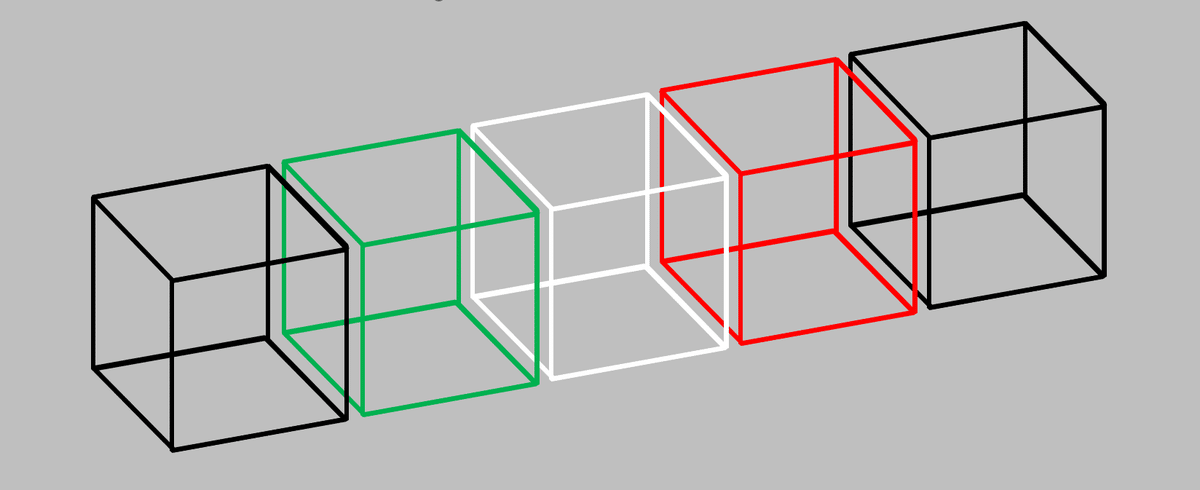
では、Tesseract内部にはこれと同じような直線に並ぶ関係になっている立方体の組(グループ)が全部で何組あるのでしょう?そして、各々の直線どうしは、どういう空間配置なのでしょうか。
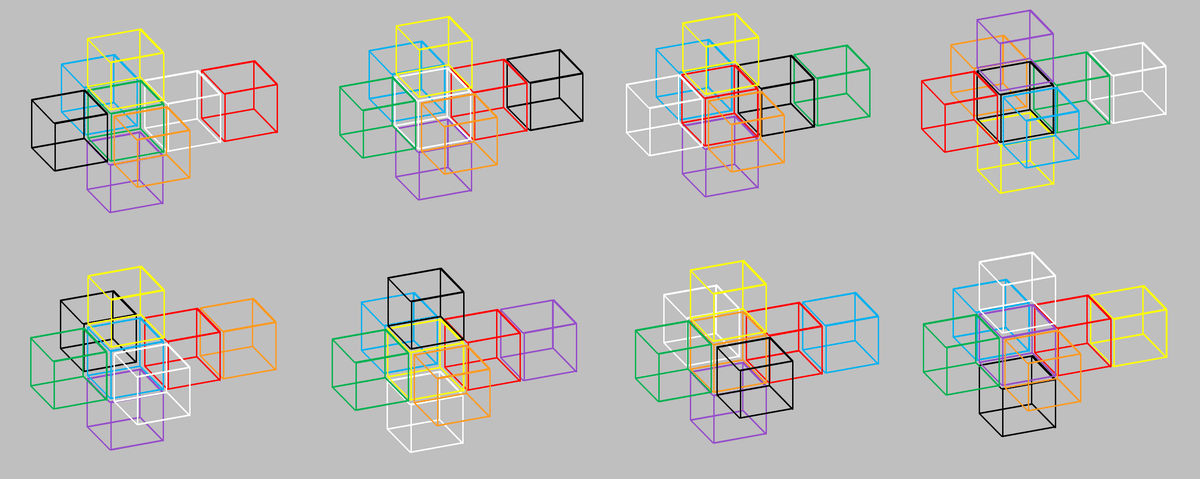
私が独自に調べてみました!
全部で6組の「直線状の並び」が、Tesseractの内部に存在することがわかりました。
緑白赤黒緑白赤黒・・・・・
黄白紫黒黄白紫黒・・・・・
青白橙黒青白橙黒・・・・・
青緑橙赤青緑橙赤・・・・
黄緑紫赤黄緑紫赤・・・・
黄青紫橙黄青紫橙・・・・
これら6本の直線状に並ぶ立方体の組み合わせたちは、とりあえず「白立方体」を中心に置いて図示してみると、次の図のような空間的位置関係になっています。

3本のXYZ直線と、3本のドーナツ状直線で合計6本です。
ぐるっと回ってるドーナツ形(Torus型)の直線って、いったいどういうわけよ?とも思います。
しかし、Tesseractにとっては、「理論上」この部分は「直線です」。
ちょっとムカつきます。
こういうトポロジーって本当に、気持ちが、モヤモヤしますね。
*Tesseractの話をしているはずだったのに、完成した図はルービックキューブを暗示するみたいな図になってるのも、面白いですよね。
いや、ただ、面白いっていうだけで、それ以上何かあるわけではないんですけれど。
あと、今回は「白の立方体」を中心にした場合は、という説明図を作ったわけですけれど、Tesseractを構成する単位図形「立方体」8個は等価なので、他の7個どれを中心に置いても、同様な結果が得られます。
どの立方体を中心にしてみても、6組の「立方体の組み合わせ」は変化しません。立方体の仲間(グループ)は変わらないです。
*どの立方体を中心に置いたかによって、6組の「直線」の空間配置と・みための形状が順繰りに変化します。
いいなと思ったら応援しよう!

