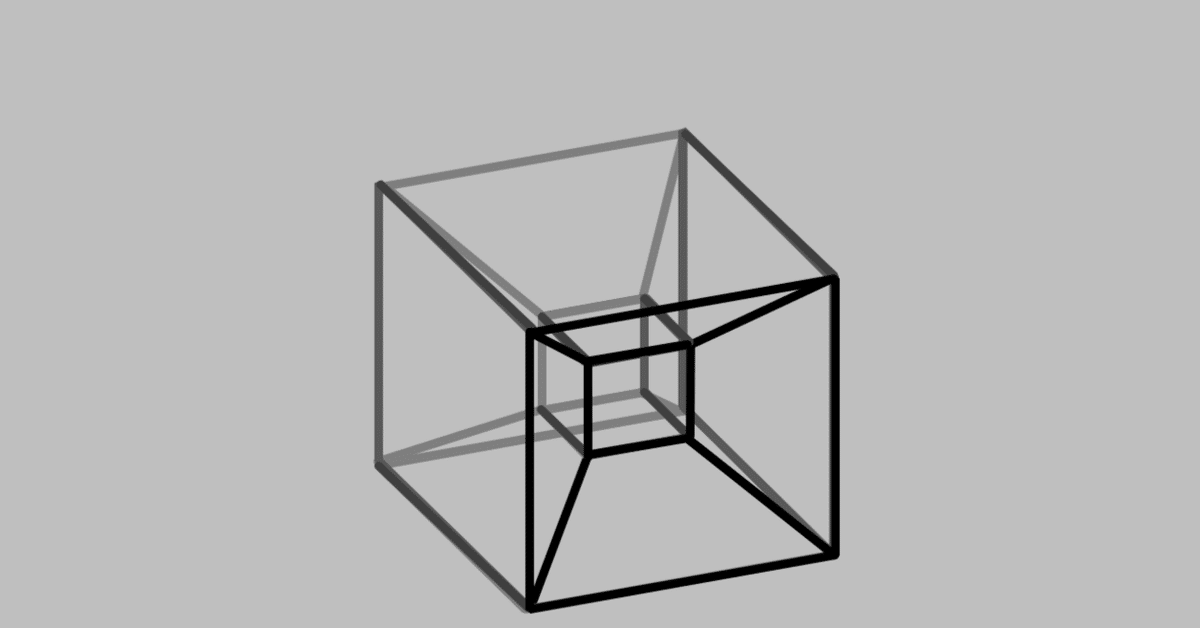
4次元・超立方体 Tesseract 今まで、ぼんやりの理解で放っておいたけど、真剣に再考察してみた（１）
４次元・超立方体（Tesseract, Hypercube, 正八胞体）はきっと大学の数学科では「知ってて当然の基礎知識」扱いなのではないでしょうか（想像）。
でも私を含め、全人類の９９％の人は「なんかそういう仮想立体もあるんだってね。知らんけど。」ということで真剣に考えたことはないと思います。
今回は、数学科ではなくて化学系の大学を卒業した一般人（？）が、Tesseractをマジに考察してみた。そしたら、なお一層、理解が深まったという話です。
＊
予告： この記事は、後半部分が有料です。
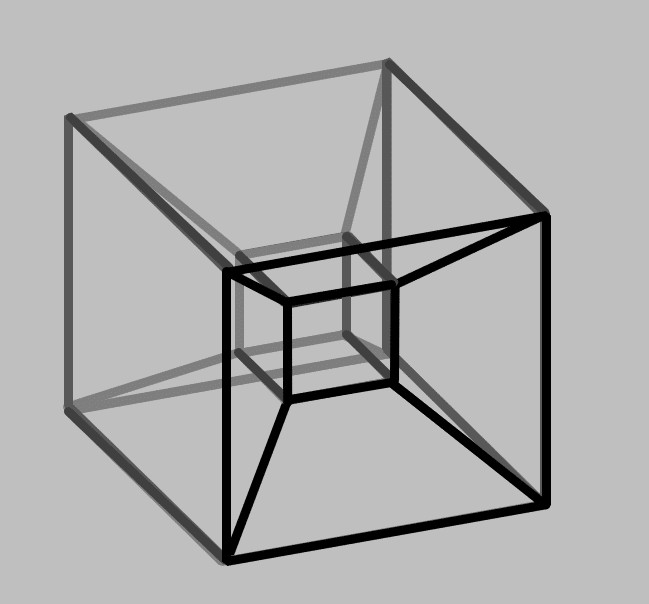
まず下準備として「面」の概念にお付き合いください。
下の図は、線分４本によって示した「正方形の展開図」です。
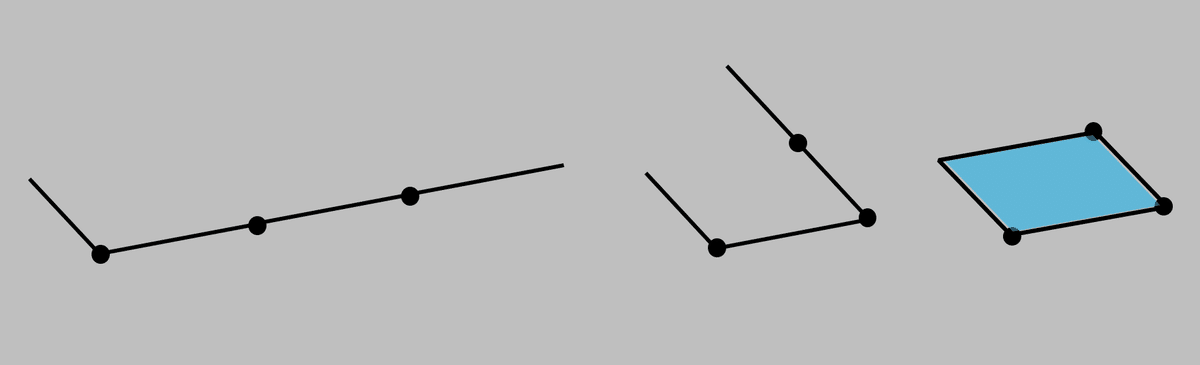
線分４本を、点（図では●印）の部分で「折り曲げ」ます。
線分４本によって「囲んで閉じた空間を作る」と、「１次元に住む生物にとって、絶対に理解できない新概念」である、面（水色で着色）が出現します。
同じ内容をもういちど別のコトバで言い直します（しつこい？）。
線分４本で「囲んで閉じた空間」を作ると、より高い次元の生物でないと理解不可能な「面」が新しく生み出されます。概念的に大げさに言い直すと、ある低次元の単位図形を、約４個使って「閉じた空間を作る」と、その内部空間に１次元単位ぶん高次元の存在＝新しい概念図形が生まれる。ということです。
これ、とても重要なことを書いたつもりです。
この考え方を３次元に適用してみましょう。
下の図は、面（正方形）６個による「立方体の展開図」です。
正方形６個を、線の部分で折り曲げ、「囲んで閉じた空間を作る」と、そこに新しい概念（新しい図形）として「胞」が出現しました。
胞は、水色で示された部分のことです。
2次元の図形の「正方形」を６個使い、完全に閉じた空間を作ると、いままでと全く違う概念「胞」が誕生したわけです。
注意：
「胞」って、要するに立方体のことでしょ？立方体って言えばいいじゃん。と感じている方もいると思います。
この文章では「平面世界では、まったく思いつくことも不可能だった新しい概念 「胞：ホウ」 が誕生しました」という説明をしたいのです。そのために、意図的に立方体という用語を使わずに「胞」で通します。
胞は立方体と同義なのですけど、「概念的存在」として扱う場合は「胞」と言うべきだと思っています。立方体って言ってしまうと、概念の方でなく、具体的にそこにある「四角い積み木の物体」と勘違いしてしまう恐れがありませんか。
はい、ということで、いよいよ４次元・超立方体の説明を試みます。
まずは立方体６個を、先の正方形６個の時みたいに並べてみます。これが「４次元・超立方体」の展開図に相当するものだと想像してみます。
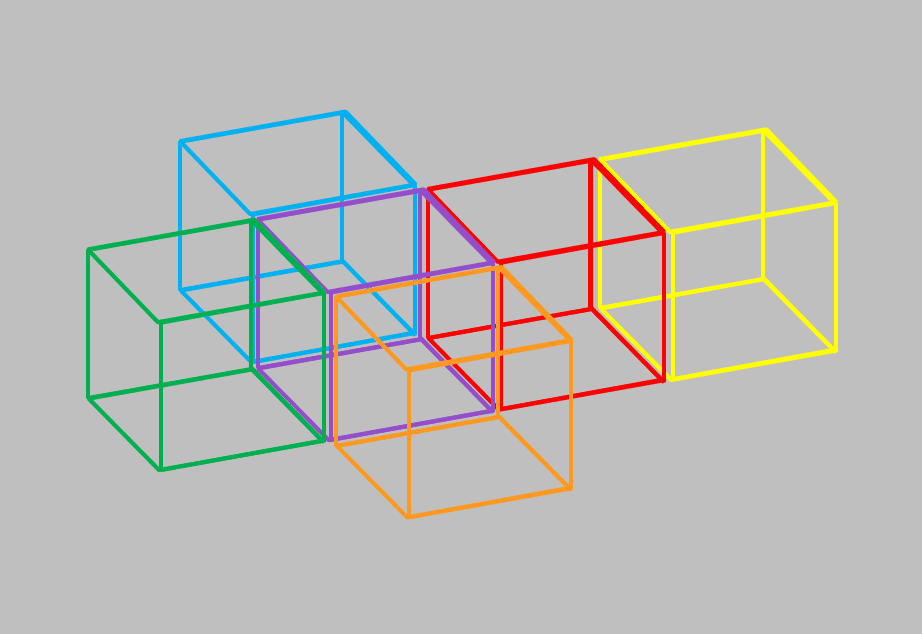
これらの６個の立方体を 「正方形から立方体を作る時と同様のうごき」で、「折りたたんで」、「囲んで閉じた空間を作ろう」と試みてみます。
すでにお気づきの通り、３次元空間でこれを実際にやってみるのは絶対に不可能です。
思考実験として、アタマの中でしか実行できません。
立方体と立方体どうしが接している面のところをオリセンとみなして「折り曲げる」？という概念はとても奇妙ですし、我々の住む実世界では、面の位置で立方体を折り曲げるのは不可能です。
でも、もしも、面を折り目の境界として折り曲げられたなら、それぞれ６個の立方体の相互の位置関係はどう変化するの？と考察すると、このような図が描けます。
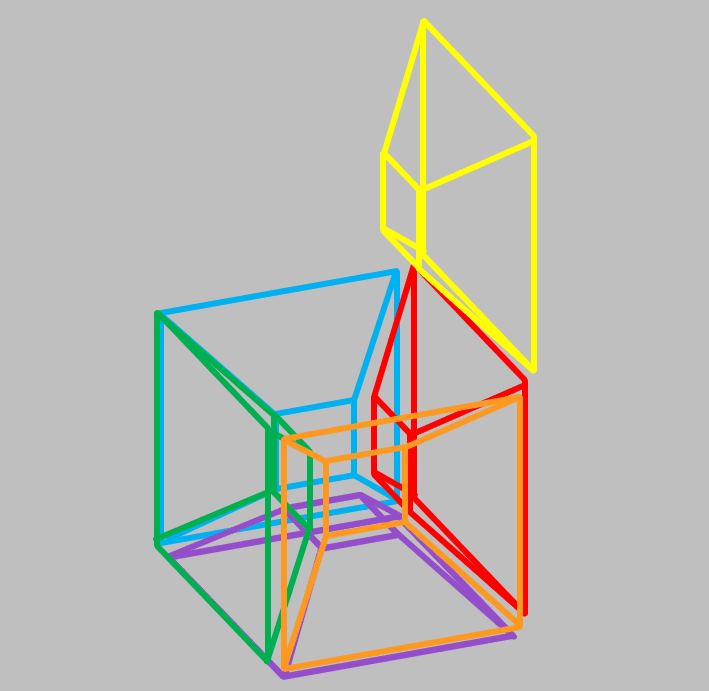
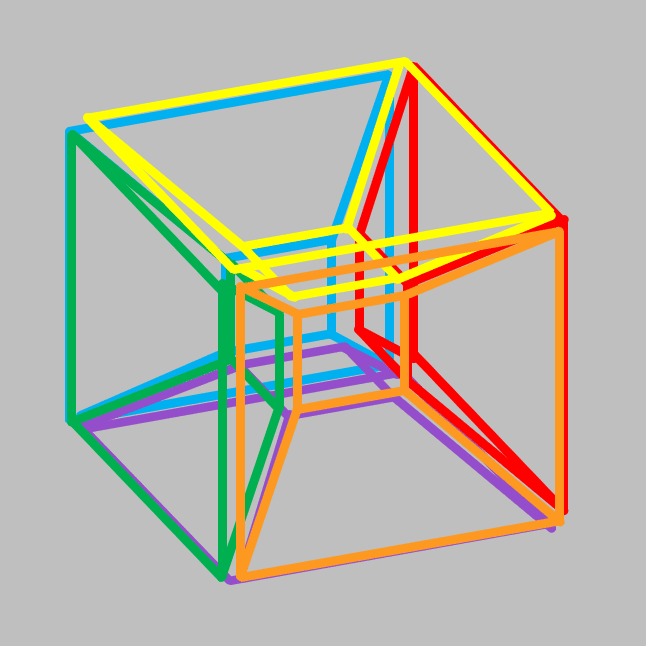
たとえば、緑の立方体の「天井（上面）」は、黄色の立方体の「西（左）側面」と接しています。
図を見てわかる通り、６つの「立方体」を「折り曲げたコト」によって内部空間が閉じたみたい？ですよね。空間が完全に閉じたような気がします。では、この図形の中心部分に新しい図形概念が発生したでしょうか？
図をしっかり見ればみるほど、中心部にある「図形」は、単なる立方体形状、すなわち立方体型の「胞」でしかないです。６つの立方体で閉じた空間を作ると、そこには「胞」ができる、と？
事実として、そうなんだから仕方ないです。まずは事実に従い、白い立方体を書き加えましょう。
余談ですが、Tesseractって、実は「白あんぱん構造体」だったのですね。
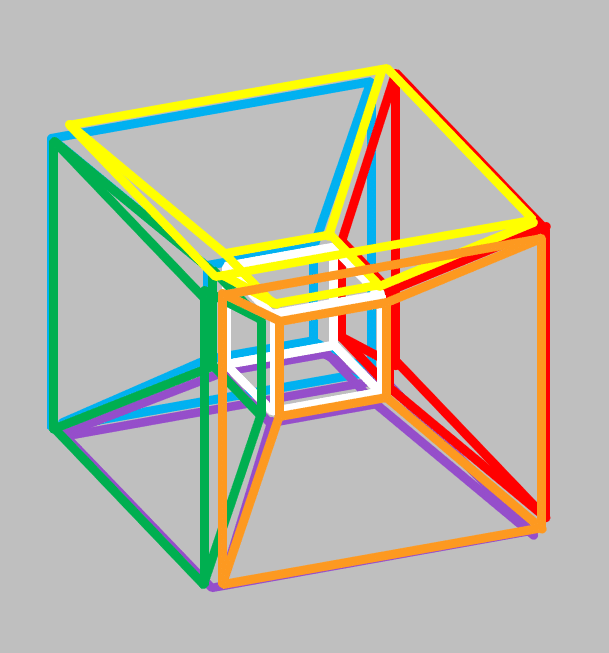
さて、立方体を６個使って空間を閉じたら、中心部に発生したのは、立方体形状の「胞」でした。・・・こんなのを納得して受け入れてはいけません。
こんな結論は矛盾であり、初期の仮定が、どこか間違っていたと考えるべきです。
なぜなら、ここまで（２次元：面、３次元：胞・・・と）論じてきた通り、立方体６個で空間を完全に閉じることに成功していた場合は、全く新しい概念だと直感的に理解できる「新図形概念」が、その位置に出現するはずだ、と、最初に仮定していたからです。
新図形概念が出現しなかった、ということはすなわち「立方体６個では、まだ４次元的空間を閉じ切ってない。４次元的な視点でみると、まだスカスカした部分が残ってるのだ」と判断されます。
だったら次は、「立方体を７個使えば、さすがに４次元的空間を完全に閉じられたんじゃないか？」という新仮説を立ててみましょう。
さて、たったいま新しく書き足した「白い立方体」を加え、全７個の立方体を用いたTesseract展開図の修正版を作ってみます。
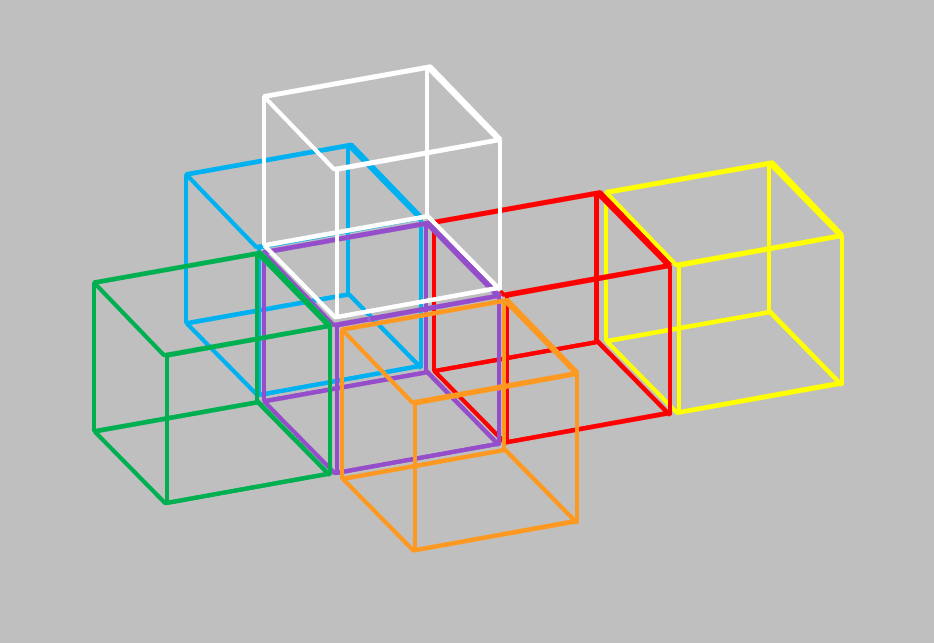
まだ続きます。
ゲームシステムのデザイナーって、何なの？どういう意味？ そんな疑問は、私の記事群によってご理解いただけるものと期待してます。 ラジくまるのアタマの中にある知識を活用していただけるお方、サポート通知などお待ちしています。