
直角二等辺三角形はパズルである。証明終わり?
本日は、平面敷き詰めパズルの話です。
ドイツの積み木?ではないですね。分類としては「木のおもちゃ」です。
MOSAIKというのがあります。こういうのなんですが・・・・

これ、じっくりよく見ると、正方形の中に正方形が見えますよね。
この正方形の作り方はとっても「イジワル」です。
***
というのも、ごく普通に「正方形を作りなさい!」って言われたら、こういうのをつくりませんか?ごく自然に。

ところが、こんな風に正方形を構成することもできるわけです。

ということをふまえて。イジワルなパズル作家は、こんな風に問題を作るわけですよ。

第1問
18個のピースをぴったり緑色のシカクの中に入れなさい。ピースどうしを上下に重ね合わせるのは禁止です。ピースはちゃんと紙面に触れた状態が正解です。
第2問
緑色のシカクの隣に、ひとまわり小さくなったピンクのシカクがあります。
このピンクのワクの内部に、可能な限りたくさんの個数のピ-スを入れなさい。ピースどうしを上下に重ね合わせるのは禁止です。ピースはちゃんと紙面に触れた状態が正解です。
ヒント:正解は13個ではないですよ。もっと数多く入ります!
***
こんな風に文章問題をつけてパズル販売されたとしたら、それはイジワル商品の完成です。
そもそも、ニンゲンというのは成功体験に非常に弱いです。
第1問をいったん正解してしまうと、その成功体験が強く印象に残り、第2問の正解のカタチを容易には発想できないというオトシ穴に落ちやすいです。
*ご注意:
この記事を読んでしまった読者のみなさんは、この「オトシ穴」にハマってみるという楽しい体験ができなくなってしまいました。
皆さんからパズルの楽しみを奪ってしまったこと。なにとぞお許しください。
上に書いたイジワル問題は、機会がありましたらぜひ、小学校4年生以上~オトナの方に出題してみてください。
***
さて、話をもとのMOSAIKに戻します。
直角三角形1単位のピースだとパズルとしての歯ごたえが足りないんですけど、こんなふうに台形のピースに構成しなおすと、なんだか面白そうな感じになってきます。

ナイフみたいな形状?あるいはもっとすなおに「台形」?ともかく、ピースの形が三角形のままだと、ちょっとパズルとしては楽しくないので、このくらいまでまとめたピースを作ります。
これを使うと、それなりにむつかしいパズルになります。
*対象年齢は小学校4~5年生くらいの想定です。
*パズルとして遊ぶ際には「台形」に描かれている線は必ずナシでお願いします。ヒントになっちゃうので。
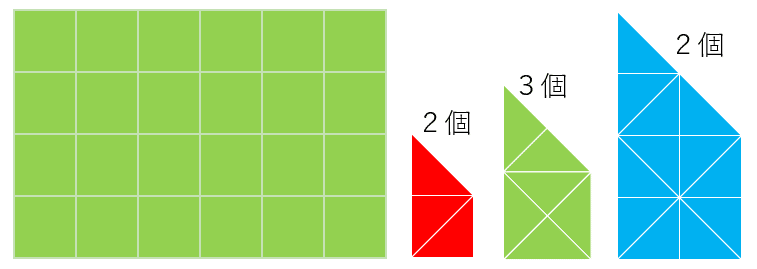
この程度ではまだカンタンすぎる。もっと歯ごたえがあるのが欲しい!
などと言われたら、下のように合体させたピースを数個まぜれば、難易度をちょっとアップさせることもできます。

というわけで、この不思議な台形を使って、どなたか「夏休みの自由研究:図形のふしぎ」とか、やってみませんか?お願いだからやってみてほしいなあ。と、思うのです。
この記事が、お子様たちにとって数学への誘いになってくれればいいなあと期待しています。
いいなと思ったら応援しよう!

